摘 要： 從串?dāng)_的原理及串?dāng)_和差分阻抗之間的內(nèi)在聯(lián)系出發(fā),，通過模型變換和公式推導(dǎo),，給出了近端串?dāng)_系數(shù)和差分阻抗之間的關(guān)系式。再以平衡結(jié)構(gòu)的帶狀線為例,，得到了平衡結(jié)構(gòu)帶狀線的近端串?dāng)_的估算公式,。在相同條件下與Hyper Lynx仿真軟件結(jié)果進(jìn)行比較，驗證發(fā)現(xiàn)估算結(jié)果與仿真結(jié)果基本符合,。
關(guān)鍵詞： 近端串?dāng)_,；差分阻抗；帶狀差分線,；前仿真
隨著半導(dǎo)體工業(yè)的飛速發(fā)展,，具有高集成度,、高速接口的器件在電子產(chǎn)品中的應(yīng)用越來越廣泛，由此產(chǎn)生的信號完整性問題也越來越復(fù)雜,。串?dāng)_是信號完整性問題中的一類關(guān)鍵問題,。串?dāng)_是指一個網(wǎng)絡(luò)通過耦合在另外一個網(wǎng)絡(luò)產(chǎn)生了有害的噪聲。通常把噪聲源所在的網(wǎng)絡(luò)稱為攻擊網(wǎng)絡(luò)或攻擊線,，而把有噪聲產(chǎn)生的網(wǎng)絡(luò)稱為受害網(wǎng)絡(luò)或受難線,。在物理空間中任何兩個網(wǎng)絡(luò)之間都會存在串?dāng)_，而且串?dāng)_不僅會發(fā)生在網(wǎng)絡(luò)的信號路徑上,，還會產(chǎn)生在信號的返回路徑上,。串?dāng)_產(chǎn)生的根本原因是由于存在邊緣場，根據(jù)麥克斯韋定律,，只要有電流存在,，就會有磁場存在。當(dāng)兩個磁場相距很遠(yuǎn)時,，磁場干擾很微弱,，基本可以忽略；但是當(dāng)兩個網(wǎng)絡(luò)相距很近時,，其中一個網(wǎng)絡(luò)的磁場就會在另一個網(wǎng)絡(luò)的信號路徑或信號返回路徑上產(chǎn)生磁場干擾,，這個干擾就是串?dāng)_的來源。
通常用n節(jié)集總電路模型來描述串?dāng)_(如圖1所示)[1],。在這個模型中存在兩條傳輸線,，傳輸線１用單位長度電容CL1和單位長度電感LL1表示，傳輸線２用單位長度電容CL2和單位長度電感LL2來表示,。它們之間的容性耦合用單位長度互容CmL表示,，感性耦合用單位長度互感LmL表示。
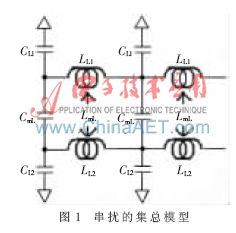
根據(jù)測量端的不同,，串?dāng)_又可以分為近端串?dāng)_和遠(yuǎn)端串?dāng)_,。近端指受害網(wǎng)絡(luò)上靠近攻擊網(wǎng)絡(luò)驅(qū)動器的一端，遠(yuǎn)端指遠(yuǎn)離攻擊網(wǎng)絡(luò)驅(qū)動器的一端,。近端串?dāng)_和遠(yuǎn)端串?dāng)_出現(xiàn)的噪聲形式不同,。近端噪聲的特性是迅速上升到一個飽和值，并且保持該值2TD時間,，然后再下降,。這個恒定的近端噪聲飽和量就稱為近端串?dāng)_系數(shù)。通常計算和仿真的就是近端串?dāng)_系數(shù)[2],。
另外,，當(dāng)兩根導(dǎo)線靠近時，差分阻抗會變小,；當(dāng)兩根導(dǎo)線遠(yuǎn)離時,，差分阻抗就會變大。這種變化的背后就是差分線間的互容互感,，而串?dāng)_的來源就是互容互感,。因此可以通過對差分線模型的研究來尋找一種可靠、快速的近端串?dāng)_算法,。本文從常見的差分阻抗公式入手,，通過建模和算法變換得到CmL/CL和LmL/LL的取值范圍，然后再估算出近端串?dāng)_系數(shù)的取值范圍,。
1 近端串?dāng)_算法
常用的近端串?dāng)_系數(shù)計算公式[3]：
從上式可以發(fā)現(xiàn),，近端串?dāng)_系數(shù)是一個百分比，由比值CmL/CL和LmL/LL組成,。如果能夠得到CmL/CL和LmL/LL的值,，或者知道它們的取值范圍，就可以知道近端串?dāng)_系數(shù)的值或者取值范圍,。一般情況下可以通過仿真軟件提取到相關(guān)的參量值,。但是使用仿真軟件來做串?dāng)_仿真需要建立專門的仿真工程，會比較麻煩,，而且有時還會碰到軟件許可等問題,。
在了解差分阻抗之前，首先了解一下傳輸線阻抗的定義,。通常阻抗定義為電壓與電流之比,。在傳輸線中，這個定義仍然有效,，傳輸線上任何一處的瞬時電壓與瞬時電流成正比,，流過傳輸線的瞬時電壓和瞬時電流的比值就稱為瞬態(tài)阻抗。傳輸線的瞬態(tài)阻抗僅由傳輸線的橫截面和材料特性共同決定,，瞬態(tài)阻抗等于施加的電壓與流過器件的電流的比值。特性阻抗是傳輸線的固有屬性,，僅與材料特性,、介電常數(shù)、頻率有關(guān),，而與傳輸線的長度無關(guān),。只要這兩個參數(shù)不變，瞬態(tài)阻抗就是一個常數(shù),。對于一個均勻的傳輸線,，任何一處的瞬態(tài)阻抗都是相同的，這樣一個恒定的瞬態(tài)阻抗就稱為傳輸線的特性阻抗[4],。
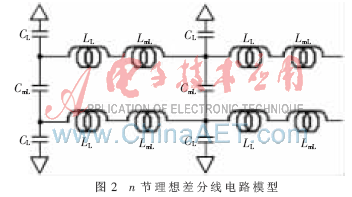
差分阻抗就是差分信號的特性阻抗,，它等于差分信號電壓與電流的比值,。如果差分線之間相距很遠(yuǎn)，它們之間的耦合會小到可以忽略不計,，差分阻抗就可以近似等于兩個單根信號阻抗之和,。當(dāng)差分信號線逐步靠近時，它們之間的邊緣場就會互相覆蓋,，相互的耦合程度就會越來越強(qiáng),。假設(shè)圖1中傳輸線１和傳輸線２相同，即CL1=CL2,，LL1=LL2,，同時傳輸線上傳送的是差分信號，那么串?dāng)_的n節(jié)集總電路模型就與差分線的n節(jié)集總電路模型相同,?？梢园褕D1的模型轉(zhuǎn)換成圖2的n節(jié)理想差分線電路模型[5]。
將圖2的模型簡化,，就可以得到圖3所示的理想的差分線集總電路模型,。
2 驗證
為了驗證估算式(11)的準(zhǔn)確性，選用Mentor的Hyper Lynx來做對比試驗,。驗證對象選擇常見的帶狀差分線（如圖4所示）,，其由兩根相互平行的導(dǎo)線和兩個包裹它們的參考平面組成。帶狀差分線設(shè)置：線寬w=4 mil,，參考平面之間的距離b=12 mil,，銅厚t=0.5 oz。帶狀線長度分別取為1 in,、2 in,、4 in、8 in,。
實驗激勵信號源設(shè)置：Vo=3 V,，r/f=1 ns。
驗證的結(jié)果如表1所示,。從表1可以看到,，當(dāng)耦合長度小于飽和長度時，近端串?dāng)_系數(shù)與耦合長度正相關(guān),；當(dāng)耦合長度大于飽和長度后,，近端串?dāng)_系數(shù)不再增加，保持一個常量,。這個結(jié)果和近端串?dāng)_的特性相吻合,。
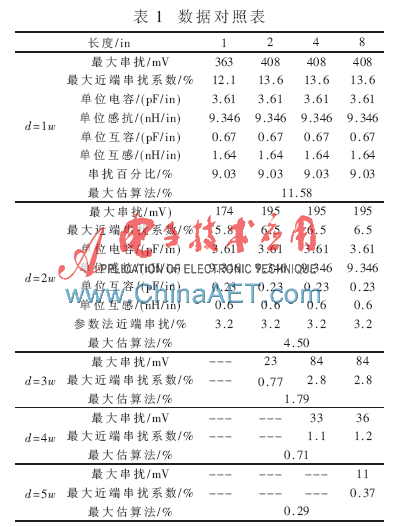
將估算結(jié)果與仿真結(jié)果進(jìn)行比對。從仿真結(jié)果中提取兩組參數(shù)，其中一組是最大串?dāng)_,，另一組是提取了單位長度的LmL,、LL、CmL和CL的參數(shù),。從這兩組數(shù)據(jù)分別得到最大近端串?dāng)_系數(shù)結(jié)果和參數(shù)法近端串?dāng)_系數(shù)結(jié)果,。將估算法的結(jié)果和上述兩組結(jié)果比較后發(fā)現(xiàn)，估算值介于最大近端串?dāng)_系數(shù)和參數(shù)法近端串?dāng)_系數(shù)之間,。這個結(jié)果與預(yù)期的結(jié)果相吻合,。最大近端串?dāng)_系數(shù)由于考慮了最惡劣的環(huán)境，會在真實的結(jié)果上放大,，保證有足夠的裕量,，因此會比估算值大。估算值本身考慮了取值的區(qū)間,，它在兩頭的取值都以極限的形式存在,，因此它的最大值會比參數(shù)法計算的結(jié)果大。
經(jīng)過驗證,，估算法確實達(dá)到了預(yù)期的效果,，它可以提供相對準(zhǔn)確的估算結(jié)果，而且使用簡便快速,，是仿真方法無法比擬的,。當(dāng)然估算法也有一些缺陷，它與實際結(jié)果之間還是有一些誤差,，而且公式也有一定的適用范圍,，不適用于耦合過程中電場變化和磁場變化比較大的情況，除非加矯正系數(shù),。在今后的研究中,，需要不斷地對其進(jìn)行補(bǔ)充和完善，使其保持速度優(yōu)勢的情況下進(jìn)一步提高結(jié)果的精確性,。
參考文獻(xiàn)
[1] BOGATIN E.信號完整性分析[M].李玉山,，李麗平，譯.北京：電子工業(yè)出版社,，2005.
[2] JOHNSON H,，GRAHAM M.High-speed digital design[M]. New Jersey：Prentice Hall PTR，1993.
[3] JOHNSON H.High speed signal propagation[M].New Jersey：Prentice Hall PTR,，2003.
[4] 陳偉，黃秋元,，周鵬.高速電路信號完整性分析與設(shè)計[M]. 北京：電子工業(yè)出版社,，2009.
[5] 梁昌紅，王新穩(wěn)，李延平,，等.微波技術(shù)與天線[M].北京：電子工業(yè)出版社,，2011.
[6] 鄭君里，應(yīng)啟衍,，楊為理.信號與系統(tǒng)(第3版)[M].北京：電子工業(yè)出版社,，2011.