0 引言

　　快速傅里葉變換(FFT" title="FFT">FFT)在雷達(dá),、通信和電子對抗等領(lǐng)域有廣泛應(yīng)用,。近年來現(xiàn)場可編程門陣列(FPGA" title="FPGA">FPGA)的飛速發(fā)展，與DSP技術(shù)相比,，由于其并行信號處理結(jié)構(gòu),，使得FPGA能夠很好地適用于高速信號處理系統(tǒng)。由于Altera等公司研制的FFT IP核,，價(jià)錢昂貴,，不適合大規(guī)模應(yīng)用，在特定領(lǐng)域中,，設(shè)計(jì)適合于自己領(lǐng)域需要的FFT處理器是較為實(shí)際的選擇,。

　　本文設(shè)計(jì)的FFT處理器，基于FPGA技術(shù),，由于采用移位寄存器" title="移位寄存器">移位寄存器流水線結(jié)構(gòu),，實(shí)現(xiàn)了兩路數(shù)據(jù)的同時(shí)輸入，相比傳統(tǒng)的級聯(lián)結(jié)構(gòu),，提高了蝶形運(yùn)算單元的運(yùn)算效率,，減小了輸出延時(shí)，降低了芯片資源的使用,。在OFDM系統(tǒng)的實(shí)際應(yīng)用中,，因它可以采用快速傅里葉變換，能方便快捷地實(shí)現(xiàn)調(diào)制和解調(diào),，故結(jié)合MIMO技術(shù),，設(shè)計(jì)的FFT處理器結(jié)構(gòu)，可以很好地應(yīng)用于2根天線的MIMO-OFDM系統(tǒng)中,。

　　1 FFT處理的應(yīng)用及DIF FFT算法原理

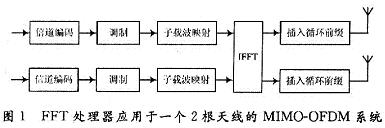
　　圖1給出一個(gè)2根天線MIMO-OFDM系統(tǒng)中FFT的使用,。快速傅里葉變換算法基本上分為兩大類：時(shí)域抽取(DIT)和頻域抽取(DIF),，這里設(shè)計(jì)的FFT處理器采用基-2 DIF算法,。

　　對于N點(diǎn)序列x(N)，其傅里葉變換

　　將x(n)分成上,、下兩部分,，得：

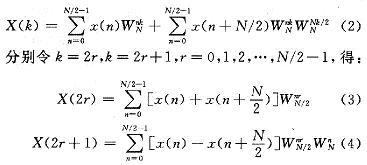
　　這樣將兩個(gè)N點(diǎn)的DFT分成兩個(gè)N／2點(diǎn)的DFT，分的方法是將x(k)按序號k的奇,、偶分開,。通過這種方式繼續(xù)分下去，直到得到兩點(diǎn)的DFT,。采用DIF方法設(shè)計(jì)的FFT,，其輸入是正序，輸出是按照奇偶分開的倒序,。

　　2 移位寄存器流水線結(jié)構(gòu)的FFT

　　在傳統(tǒng)流水線結(jié)構(gòu)的FFT中,，需要將全部數(shù)據(jù)輸入寄存器后,，可開始蝶形運(yùn)算。在基-2 DIF算法中可以發(fā)現(xiàn),，當(dāng)前N／2個(gè)數(shù)據(jù)進(jìn)入寄存器后，運(yùn)算便可以開始,，此后進(jìn)入的第N／2+1個(gè)數(shù)據(jù)與寄存器第一個(gè)數(shù)據(jù)進(jìn)行蝶形運(yùn)算,，以此類推。

　　由于采用頻域抽取法,，不需要對輸入的數(shù)據(jù)進(jìn)行倒序處理,，簡化了地址控制，這樣,，可以采用移位寄存器的方式,，依次將前N／2個(gè)數(shù)據(jù)移入移位寄存器，在N／2+l時(shí)刻,，第一個(gè)數(shù)據(jù)移出移位寄存器,，參與運(yùn)算。相對于傳統(tǒng)的RAM讀寫方式,，采用移位寄存器存儲結(jié)構(gòu)綜合后的最大工作頻率為500 MHz,，遠(yuǎn)大于RAM方式的166 MHz。

　　當(dāng)移位寄存器相繼有數(shù)據(jù)移出時(shí),，在移位寄存器中會出現(xiàn)空白位,。此時(shí)，引入第二路數(shù)據(jù),，在第一路數(shù)據(jù)依次移出進(jìn)行蝶算時(shí),，第二路數(shù)據(jù)依次補(bǔ)充到移位寄存器的空白位中，為運(yùn)算做準(zhǔn)備,。通過這樣一種類似“乒乓操作”的結(jié)構(gòu),，可以使蝶形運(yùn)算模塊中的數(shù)據(jù)不間斷地輸入，運(yùn)算效率達(dá)到100％,。不同于傳統(tǒng)的“乒乓操作”結(jié)構(gòu),，由于使用移位寄存器，不需要兩塊RAM,，可以省掉一半的寄存器,。圖2為256點(diǎn)FFT處理器的第一級結(jié)構(gòu)。

　　基于上述基本原理,，將這種移位寄存器結(jié)構(gòu)擴(kuò)展到整個(gè)FFT系統(tǒng)的各級,，可以發(fā)現(xiàn)各級使用的移位寄存器數(shù)量是遞減的。現(xiàn)使用一個(gè)8點(diǎn)結(jié)構(gòu)來進(jìn)行說明,。

　　如圖3所示,，數(shù)據(jù)由輸入l和輸入2進(jìn)入第一級,。通過開關(guān)進(jìn)行選通控制。由于是N=8的運(yùn)算,，所以各級分別加入4級,、2級和1級的移位寄存器。

　　分兩路來說明運(yùn)算過程：

　　將K1打到位置①,，第一路數(shù)據(jù)進(jìn)入移位寄存器,，待第一路的前4個(gè)數(shù)據(jù)存入4級移位寄存器后，第一路進(jìn)入的第5個(gè)數(shù)據(jù)與移位寄存器移出的第1個(gè)數(shù)據(jù)進(jìn)行蝶形運(yùn)算,。

　　由于輸出結(jié)果有上下兩路,，第二級是一個(gè)四點(diǎn)的DFT，所以對于上路的輸出結(jié)果x0(0)+x0(4)類似于第一級,，直接存入下一級寄存器,，為四點(diǎn)運(yùn)算做準(zhǔn)備，下路的輸出,，先存入本級2級移位寄存器中,，等到上路的四點(diǎn)運(yùn)算開始，第二級的移位寄存器有空白位時(shí),，移入第二級,，為下路的四點(diǎn)運(yùn)算做準(zhǔn)備。所以第一級蝶形運(yùn)算上路輸出前N／4=2個(gè)進(jìn)入下一級寄存器,，下路輸出的數(shù)據(jù)依次存入本級移位寄存器中,。

　　當(dāng)?shù)谝患壍妮敵銮癗／4=2個(gè)數(shù)據(jù)x0(0)+x0(4)和x0(1)+x0(5)存入第二級移位寄存器時(shí)，運(yùn)算便可以開始,，這時(shí)開關(guān)K2打到位置②,，此時(shí)第一級上路輸出的數(shù)據(jù)x0(2)+x0(6)，即第一級上路輸出的第三個(gè)數(shù)據(jù)與第二級移位寄存器移出的第一個(gè)數(shù)據(jù),，即x0(O)+x0(4)進(jìn)行蝶形運(yùn)算,，輸出的第四個(gè)數(shù)據(jù)x0(3)+x0(7)與x0(1)+x0(5)進(jìn)行蝶算。在這個(gè)運(yùn)算過程中,，第一級的2級移位寄存器移出數(shù)據(jù)依次移位存入到第二級的移位寄存器產(chǎn)生的空白位中,。

　　兩個(gè)時(shí)鐘后，第一級上路輸出的四個(gè)數(shù)據(jù)完成了蝶形運(yùn)算,，K2打到位置①,，在接下來的兩個(gè)時(shí)鐘里，第一級中2級移位寄存器的輸出依次與此時(shí)第二級中2級移位寄存器的輸出數(shù)據(jù)進(jìn)行蝶形運(yùn)算,，即與,，與完成第一級下路輸出的四個(gè)數(shù)據(jù)的蝶形運(yùn)算。

　　此時(shí),，第一路在第一級運(yùn)算后的輸出數(shù)據(jù),，在第二級完成了全部的蝶形運(yùn)算,。第二級的輸出結(jié)果同第一級一樣，蝶形運(yùn)算的上路輸出前N／8=1個(gè)進(jìn)入下一級寄存器,，后一個(gè)數(shù)據(jù)直接進(jìn)入后一級進(jìn)行碟算,，下路輸出的數(shù)據(jù)存入本級移位寄存器中。

　　第三級的運(yùn)算與第二級和第一級類似,，即移入1級寄存器的數(shù)據(jù)與其后一個(gè)數(shù)據(jù)進(jìn)行碟算,，同時(shí)使前一級寄存器的輸出數(shù)據(jù)進(jìn)入后一級寄存器的空白位中，然后開關(guān)打到位置②,，對下路輸出數(shù)據(jù)進(jìn)行碟算。

　　對于第二路數(shù)據(jù),，通過開關(guān)控制,，在第二級中，待第一路第一級下路輸出數(shù)據(jù)進(jìn)行蝶形運(yùn)算時(shí),，移入寄存器的空白位,，為運(yùn)算做準(zhǔn)備，由于前級運(yùn)算周期是后級運(yùn)周期的兩倍,，對于第二級碟算模塊而言,，數(shù)據(jù)仍然是不間斷輸入的。通過這樣兩路數(shù)據(jù)的交替運(yùn)算和存儲,，實(shí)現(xiàn)“乒乓操作”,，從而提高了蝶形運(yùn)算模塊的運(yùn)算效率。圖4是256點(diǎn)FFT的具體運(yùn)算輸入和輸出時(shí)序圖,。對于只有一路數(shù)據(jù)的應(yīng)用場合,，可以在前級加入，門控開關(guān)和數(shù)據(jù)緩沖寄存器分成兩路數(shù)據(jù),，實(shí)現(xiàn)一路數(shù)據(jù)的不間斷讀入,。

　　由于采用移位寄存器結(jié)梅，各級寄存器使用的數(shù)量都是固定的,，即為N／2+N／4,。其中，N為該級DFT運(yùn)算的點(diǎn)數(shù),，各級使用的移位寄存器深度逐級遞減,，從而大大降低了寄存器的使用數(shù)量。

　　此外,，由于各級結(jié)構(gòu)固定,，所以大點(diǎn)數(shù)FFT只是小點(diǎn)數(shù)FFT基礎(chǔ)上級數(shù)的增加，而且由于移位寄存器的輸出相對于RAM而言不需要復(fù)雜的地址控制,，所以這種結(jié)構(gòu)的FFT處理器具有非常好的可擴(kuò)展性,。比如需要實(shí)現(xiàn)512點(diǎn)的FFT,，只需要在256點(diǎn)的基礎(chǔ)上增加一級即可。

 3 具體模塊的設(shè)計(jì)

　　3．1 控制與地址產(chǎn)生模塊

　　由于兩路數(shù)據(jù)同時(shí)輸入,，為了防止發(fā)生兩路數(shù)據(jù)間的串?dāng)_,，對數(shù)據(jù)的控制顯得極其關(guān)鍵。從上面的算法結(jié)構(gòu)分析中知道,，由于后級的DFT運(yùn)算點(diǎn)數(shù)是前一級的一半,，所以后一級的開關(guān)轉(zhuǎn)換周期也是前一級的一半，基于這種關(guān)系,，可以使用一個(gè)8位計(jì)數(shù)器的每一位狀態(tài)來對各級開關(guān)進(jìn)行控制,。最高位控制第一級，同時(shí)由于上一級數(shù)據(jù)進(jìn)入下一級需要一個(gè)時(shí)鐘,，所以下一級的開關(guān)轉(zhuǎn)換時(shí)刻要比上一級延遲一個(gè)時(shí)鐘周期,。

　　對于移位寄存器，在實(shí)現(xiàn)時(shí),，各級的前級移位寄存器深度為N／2-1,，從本質(zhì)而言，是使運(yùn)算開始的時(shí)鐘上升沿到來時(shí),，數(shù)據(jù)已經(jīng)出現(xiàn)在碟算模塊輸入線上,，而不需要下一個(gè)時(shí)鐘的驅(qū)動來移出寄存器，比如第二級移位寄存器的級數(shù)為63,。這樣,，運(yùn)算周期正好是2的倍數(shù)，從而方便使用計(jì)數(shù)器的各位直接對開關(guān)進(jìn)行控制,。

　　同時(shí),，計(jì)數(shù)器還可以用來產(chǎn)生所需旋轉(zhuǎn)因子的RAM地址。根據(jù)各級蝶形運(yùn)算所需旋轉(zhuǎn)因子的規(guī)律,，可以利用計(jì)數(shù)器的高位補(bǔ)零來產(chǎn)生查找表的地址,。比如，對于第一級,，因?yàn)樾枰谧畹臀坏谝淮纬霈F(xiàn)1時(shí)提供,，第二次出現(xiàn)1時(shí)提供，…,，以此類推,，周期為128，所以可以使用計(jì)數(shù)器的低七位作為地址,。對于第二級,，由于所需要的地址為偶數(shù)，可以由計(jì)數(shù)器的[6：1]和最低位置O產(chǎn)生。表l為8點(diǎn)時(shí)使用三位計(jì)數(shù)器輸出旋轉(zhuǎn)因子的地址情況,。

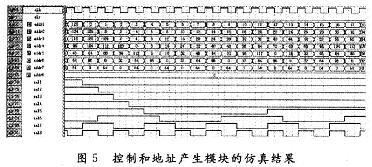
　　控制和地址產(chǎn)生模塊的仿真結(jié)果如圖5所示,，其中sel代表開關(guān)控制，addr代表產(chǎn)生的地址,。

　　3．2 蝶形運(yùn)算模塊

　　蝶算模塊由一個(gè)復(fù)數(shù)加法器,，一個(gè)復(fù)數(shù)減法器和一個(gè)旋轉(zhuǎn)因子的復(fù)數(shù)乘法器構(gòu)成，如圖6所示,。

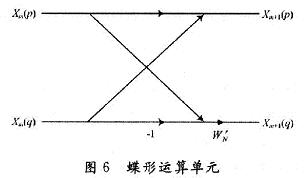
　　旋轉(zhuǎn)因子乘法器通常由4次實(shí)數(shù)乘法和2次加／減法運(yùn)算實(shí)現(xiàn),，但因?yàn)閏os和sin的值可以預(yù)先存儲，通過下面的算法可以簡化復(fù)數(shù)乘法器：

　?。?）存儲如下三個(gè)系數(shù)：C,，C+S，C-S

　?。?）計(jì)算：E=X-Y和Z=C*E=C*（X-Y）

　?。?）用R=（C-S）*Y+Z，I=（C+S）*X-Z,，

　　得到需要的結(jié)果,。

　　這種算法使用了3次乘法,，1次加法和2次減法,，但是需要使用存儲3個(gè)表的ROM資源。

　　設(shè)計(jì)中數(shù)據(jù)的輸入為16位復(fù)數(shù),，所以將旋轉(zhuǎn)因子cos(2kπ／N),，sin(2kπ／N)量化成帶符號數(shù)的16位二進(jìn)制數(shù)后，存儲到ROM中,，由于值域不同,，需要注意C+S和C-S的表要比C表多1位精度。

　　運(yùn)算后的結(jié)果需要除以量化時(shí)乘以的倍數(shù)16b011111llllllllll,。具體實(shí)現(xiàn)時(shí)由于除法運(yùn)算在FPGA器件需要消耗較多的資源,，設(shè)計(jì)中采用二進(jìn)制數(shù)移位的方法來實(shí)現(xiàn)除法運(yùn)算。為了防止數(shù)據(jù)溢出,，設(shè)計(jì)對輸出結(jié)果除以2,。圖7為蝶形運(yùn)算模塊的RTL級結(jié)構(gòu)圖。

　　3．3 倒序輸出模塊

　　由頻域抽取的基-2算法可知,，運(yùn)算結(jié)果需要倒序輸出,。可以先將結(jié)果存儲到RAM中,，然后使用O～255的二進(jìn)制數(shù)倒序產(chǎn)生RAM讀取地址,，依次將結(jié)果讀出，其中實(shí)現(xiàn)一個(gè)8位二進(jìn)制數(shù)倒序的算法如下：

　　(1)將8位數(shù)字的相鄰兩位交換位置；

　　(2)將相鄰的兩位看作1組,，相鄰兩組交換位置,；

　　(3)將相鄰的4位看作1組，相鄰兩組交換位置,。

　　經(jīng)過這樣的交換位置后,，輸出即為原來8位二進(jìn)制數(shù)的倒序。

　　舉例對于8位二進(jìn)制數(shù)10110110來說,，第一次交換位置的結(jié)果是01111001,，第二次交換位置的結(jié)果是11010110，最后交換位置的結(jié)果是01101101,?？梢娬檬窃瓉頂?shù)字的倒序。

　　另外,，由于設(shè)計(jì)的是兩路數(shù)據(jù)同時(shí)寫入,，一路數(shù)據(jù)讀出，所以讀取的頻率是寫入頻率的2倍,，使用PLL實(shí)現(xiàn)原始時(shí)鐘的二倍頻,，用來讀取RAM。倒序模塊仿真結(jié)果如圖8所示,。

　　最終生成的FFT處理器模塊圖如圖9所示,。

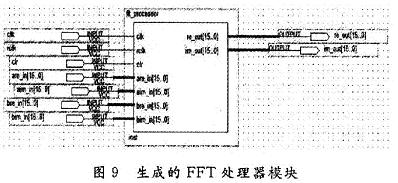
　　4 仿真結(jié)果

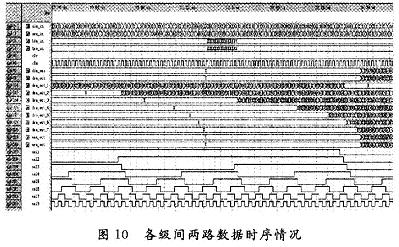
　　各級間數(shù)據(jù)時(shí)序情況如圖10所示，設(shè)計(jì)的FFT處理器仿真結(jié)果如圖1l所示,。采用一路階梯遞增信號和另一路：XXXX信號進(jìn)行仿真,，通過與Matlab計(jì)算結(jié)果進(jìn)行對比，結(jié)果基本一致,，可以滿足系統(tǒng)要求,。系統(tǒng)總的延時(shí)由延時(shí)最大的第一級決定，為第一級運(yùn)算的延時(shí)加上倒序輸出的延時(shí),，總共是(256+128)×clk,，相對于一般流水線結(jié)構(gòu)(256×讀入周期+7×128×蝶算周期+128×讀入周期)，系統(tǒng)延時(shí)大為減少,。

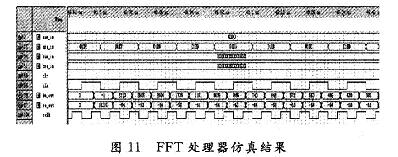
　　通過仿真可知,，系統(tǒng)最大頻率由蝶形運(yùn)算模塊的最大工作頻率決定。使用QuartusⅡ軟件時(shí)序仿真后,，得到處理器的工作頻率為72 MHz,。

　　5 結(jié)語

　　通過采用移位寄存器流水線結(jié)構(gòu)，可以有效地提高FFT處理器中蝶形運(yùn)算單元的效率,，減少寄存器的使用數(shù)量,，并且簡化了地址控制,，提高處理器的工作頻率，具有良好的可擴(kuò)展性,，同時(shí)可以實(shí)現(xiàn)兩路數(shù)據(jù)的同時(shí)輸入,，從而增大了一倍的數(shù)據(jù)吞吐量。對于工作頻率要求較高,，數(shù)據(jù)吞吐量較大,，尤其對于需要兩路數(shù)據(jù)輸入的場合，比如兩天線的MIMO-OFDM系統(tǒng),，具有很大的實(shí)用價(jià)值,。