《電子技術應用》
您所在的位置：首頁 > 模擬設計 > 設計應用 > 基于聯合字典稀疏表達的目標識別算法研究
基于聯合字典稀疏表達的目標識別算法研究
2019年電子技術應用第4期
段沛沛1，2，李 輝1,，雒明世2
1.西北工業(yè)大學 電子信息學院,，陜西 西安710029,；2.西安石油大學 計算機學院，陜西 西安710065
摘要： 在使用高分辨距離像開展目標識別時,，傳統方法很少利用樣本的稀疏性,。為了克服此類識別所面臨的繁瑣的分析難題，簡化識別過程,，稀疏分析其實是一種不錯的壓縮樣本數據,，提升剖析效果的方法。因此,，提出一種基于聯合字典及快速分解策略完成雷達一維距離像稀疏分析,，進而鑒識目標的算法,。為了提升識別策略的實用性,，算法還嘗試依信噪比調控其內稀疏分解參數，以改善算法抗噪性能,。實驗測評表明：相較同類識別策略,，該算法求解更為便捷，適用范圍有所拓展,；相比不同類型的常規(guī)識別策略,，該算法抵御噪聲的能力有所提升，識別效果更優(yōu),。
中圖分類號： TN959.1+7
文獻標識碼： A
DOI：10.16157/j.issn.0258-7998.190127
中文引用格式： 段沛沛,，李輝，雒明世. 基于聯合字典稀疏表達的目標識別算法研究[J].電子技術應用,，2019,，45(4)：11-14.
英文引用格式： Duan Peipei，Li Hui,，Luo Mingshi. Study on radar target recognition based on sparse representation with a federated dictionary[J]. Application of Electronic Technique,，2019，45(4)：11-14.
Study on radar target recognition based on sparse representation with a federated dictionary
Duan Peipei1,，2,，Li Hui1，Luo Mingshi2
1.Department of Electronics Engineering,，Northwestern Polytechnical University,，Xi′an 710029，China,； 2.School of Computer Science,，Xi′an Shiyou University,，Xi′an 710065，China
Abstract： When high resolution range profiles(HRRP) are used to recognize radar target, few traditional recognition methods analyse the sparseness of HRRP samples. In order to overcome the tedious analysis problems and simplify the recognition procedure, sparse representation is an effective way to compress HRRP samples and extract the target features. Thus, a federated redundant dictionary and a fast sparse representation algorithm are introduced to implement radar target recognition here. Moreover, a sparse decomposition parameter is adjusted by SNR in order to suppresses noise. The simulation results show that compared with the same kind of RATR algorithms, the algorithm in the paper is practicable, simple and efficient. In contrast to the traditional dimension reduction recognition method, it has better noise robustness and higher recognition ratio.
Key words : radar target recognition,；high resolution range profile,；sparse decomposition；federated dictionary

0 引言

    高分辨距離像（High Resolution Range Profile,，HRRP）樣本中蘊含目標重要信息,，但是受其自身可視性的限制，這些信息并不適宜直接用于識別[1],。為此,，必須細致地剖析HRRP樣本，盡量準確地獲取繁雜數據中的重要信息,，方可實現對目標的準確識別,。

    依據數學分析，常規(guī)信號可采用某空間（域）內的若干基函數組合來表達,。因此,，以往有不少識別算法嘗試將目標HRRP映射到某個特定域內，借助適當變換來完成對其的分析,、表達,，尤其是降維表達[2]。近年來對稀疏理論的研究發(fā)現,，想要更為精準地對特定信號開展降維分析,，其實可在考慮并衡量信號自身特征的基礎上，依據冗余度更大的基函數組合來完成,。本文就將遵循特征表示的識別思路,，依據稀疏理論，探討能夠更為簡潔且穩(wěn)健提高HRRP目標識別效果的方法,。

1 稀疏分析技術要點

    由常規(guī)正交基構成的字典種類很多,，且優(yōu)勢鮮明。目前,，其實已有不少研究針對特定的應用,，找到了與之契合、意義明確的正交基,，用以完成工作所需的信號分解及表達,。可是依此所得的分析結論并非均可推廣,，或者具備借鑒意義,。換言之，在實際信號相對復雜,，且可能具有未知特性的情況下,，僅依靠由某一確定正交基構造的字典,，往往很難保證其對信號表達的準確性，自然也無法保證變換,、表達的稀疏性,。

    為了彌補簡單正交字典的劣勢，同時又保留其優(yōu)勢,，或可嘗試借助多個正交基級聯構造冗余字典,，以達到預期表達效果。事實上,，這類研究思路已在圖像信號處理中得到了應用及驗證[3-4],。研究人員曾圍繞常用（諸如：時-頻、Meyer-Lemarié小波及傅里葉基等）級聯字典的設計和相關分解思路進行探討,，但以往此類字典大多僅借由兩種正交基組合構造,，因此為了進一步提升此類字典的表達能力，可考慮將其拓展為更多個基的組合,，以構造一類兼具正交性及過完備特點的聯合字典,，并用以實現對雷達一維HRRP信號的稀疏分析。

1.1 聯合字典

xhcl3-1.1-x1.gif

    為了滿足求解的唯一性條件,，并兼具較好的表達能力,，本文的聯合字典考慮選用一類具備良好正則性的Daubechies小波(dbN,，N為階數) ,。對于dbN小波，通常隨著N的增加,，將使得信號在依其變換后的能量愈發(fā)集中,，數據壓縮率愈高。不過,，N增大在帶來壓縮優(yōu)勢的同時,，卻削弱了其時域緊支性，影響了對樣本進行稀疏表達所涉的運算量,，制約了分析的實時操作性,。

    為此，文中在采用其構造聯合字典進行HRRP稀疏分析時,，不僅對子字典選擇進行了適當的折中處理（N=1~10）,，還嘗試探尋更為快捷的分解策略。

1.2 分解策略

xhcl3-gs1-2.gif

    依據聯合字典,，采用改進的分組匹配追蹤策略Improved Partition Matching Pursuit (IPMP)實現分解的具體步驟如下：

xhcl3-gs3.gif

xhcl3-gs4-9.gif

2 基于聯合字典稀疏表達的目標識別

    該識別算法將被劃分為兩個處理環(huán)節(jié)：前一環(huán)節(jié)主要關注如何自HRRP數據中篩選目標特征,；后一環(huán)節(jié)則關注如何利用所得識別目標。

2.1 訓練環(huán)節(jié)

xhcl3-2.1-x1.gif

    (1)采用Daubechies系列小波基構造聯合字典,。

    (2)基于樣本求取類別字典,。

    借助IPMP算法,，依聯合字典對HRRP樣本進行分解，以剔除樣本中的無用成分,，保留核心目標特征,，同時實現數據降維，求得各目標類別字典Gl(l=1,，2,，…，N),。

2.2 測試環(huán)節(jié)

    在這一環(huán)節(jié),，將借助類別字典Gl(l=1，2,，…,，N)對相應目標HRRP樣本開展稀疏分析，以判定其類別,。具體操作步驟如下：

    初始化：根據數據類型,，確定對其的校準策略，并得到測試樣本y,。

xhcl3-gs10-14.gif

3 仿真分析

3.1 仿真數據說明

    仿真環(huán)境：Windows 7系統,，CPU頻率為1.5 GHz，內存2 GB,。仿真軟件為MATLAB 2012b,。仿真中用到3類飛機目標(B-1b、B-52,、F-15型)的HRRP仿真數據,，數據設定：雷達中心頻率為5 520 MHz，帶寬400 MHz,，方位角控制在0°～180°間,，每隔0.1°采集一次回波，當俯仰角及橫滾角均為0°時,，所得樣本中等間隔篩選出600個用于訓練階段,；當俯仰角調整為3°、橫滾角也調整為3°時,，所得樣本中等間隔篩選出300個用于測試,。另外，還將在測試樣本中加入白噪聲,，以模擬不同信噪比的情況,。

3.2 實驗分析

3.2.1 訓練仿真實驗

    為了有效地對HRRP信號進行稀疏分析，字典的選擇至關重要,，而與之配合的分解算法的選擇也同樣非常關鍵,。本文依據聯合字典,，探討了一類適用的IPMP分解策略。為了說明不同字典及分解方法對于樣本表達測效果差異,，圖1中展示的是對于F-15機型同一組HRRP樣本信號,，分別依據Harr小波基或聯合字典，輔以不同分解策略,，經稀疏分析之后所得的逼近效果比對結果,。

xhcl3-t1.gif

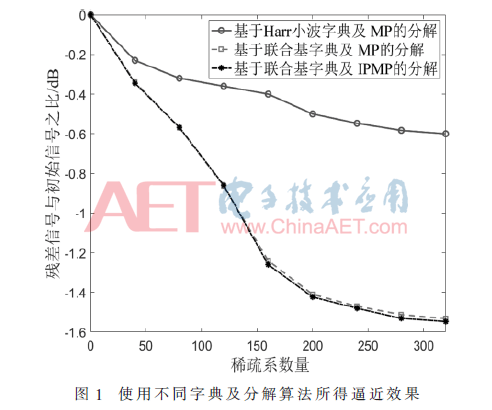
    通過圖1可知，首先,，無論采用何類字典和分解策略,，隨著所選稀疏系數的增多，對原始數據表達的誤差將逐漸減小,。不過,，減小到一定程度后，這種變化趨勢會趨于緩慢,，并趨向穩(wěn)定,。其次，比較了圖示三類方法所得逼近表述的準確性,，可以看出在使用聯合字典時,，由于其具備對多種特征的表達能力，因而適用范圍更廣,，表述效果也相對更優(yōu),，分解留存的殘差也就更小。再次,，圖中還依據同一聯合字典,，就不同分解算法性能進行了比對,。鑒于本文探討的IPMP分解方法是在常規(guī)MP方法的基礎上做了相應的修正,，改善了后者求解時可能面臨的過匹配難題，所以采用IPMP分解所得的表達準確率會適當優(yōu)于使用MP所得,。

    除去表述上的差異外,，更重要的是，使用IPMP算法將能夠更快地完成樣本分解,。表1中給出了稀疏系數量為100,、信噪比15 dB時，針對同一目標相同樣本,，分別用表內分解方法及字典進行稀疏分析時,，所耗費時間的對比關系。

xhcl3-b1.gif

3.2.2 測試仿真實驗

    無論是何種應用背景,，當樣本信噪比較高時,，識別分析效果往往相對較優(yōu),。可是,，實踐中很難保證接收信號質量,，為此所用識別策略應具備盡可能好的抵御雜噪、干擾的性能,。本實驗就此進行了算法間的比較分析,，并給出了如圖2所示的測試結果。

xhcl3-t2.gif

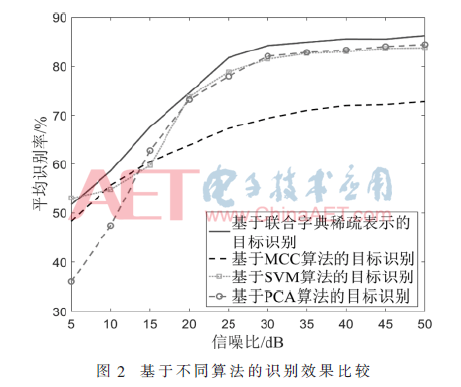
    圖2中就幾類算法的性能進行了比對,，其中本文探討的方法以及依據PCA開展的識別均可歸入依重構模型開展識別分析的類型,。不同的是，前者將依據聯合字典展開對HRRP的稀疏分析,、降維處理,，以達成識別分析的目的。相較而言,，后者其實也具備類似的“去冗余”能力,，可將HRRP樣本由高維向低維映射，并且也能保留其潛在的數據結構,，使得去冗余后的低維數據中仍然留存有原始信號的主要特征,。不過，根據以往研究,、應用也可了解到,，雖然PCA算法中基的選取至關重要，可是它本身對此卻有所制約,，不僅如此,，其主成分數量還受到信號維度大小的限制。顯然,，兩者相比,，本文所用的聯合字典不僅冗余，約束也更弱,，因此依其所得識別性能也就更優(yōu),。

    此外，本實驗還比較了MCC,、SVM識別算法的性能,，結果顯示：信噪比對各類算法的識別性能均有明顯的影響。具體而言,，SVM與本文算法相比,，兩者性能雖然在高信噪比時差別不大，但在低信噪比時卻相距甚遠，后者的抗噪能力顯然更強,。而用MCC法識別所得的準確率普遍較低,，據本文算法取得的識別結果亦是優(yōu)于采用MCC所得。不過,，有研究表明[1],，某些情況下其實可先借由對HRRP數據進行適當的冪變換預處理，再采用MCC法即可獲取較好的辨識結果,。但是,，這類冪變換可能會造成噪聲水平的放大，削弱目標分量,，反而影響了MCC法識別分析的抗噪性能,。

4 結論

    本文將稀疏分析理論引入目標識別應用，并基于分組稀疏分析策略開展了對HRRP樣本的剖析及識別,。實驗表明：基于分組稀疏分析思路的目標識別方案切實可行,，能夠用以達成對目標穩(wěn)健、有效地識別,；相比某些常規(guī)識別算法,，文中所提方法具有抵御雜噪干擾的能力及識別準確率均更優(yōu)。在當前寬帶雷達普遍應用的背景下,，文中所提算法實現過程簡捷,，大量壓縮了樣本分析量，緩解了此類識別勢必面臨的龐雜的數據處理難題,。

參考文獻

[1] 杜蘭.雷達高分辨距離像目標識別方法研究[D].西安：西安電子科技大學,，2007.

[2] 馮博，杜蘭,，張學鋒,，等.基于字典學習的雷達高分辨距離像目標識別[J].電波科學學報，2012,，27(5)：897-905.

[3] 全盛榮,，張?zhí)祢U，王俊霞,，等.基于稀疏分解的SFM信號的時頻分析方法[J].電子技術應用,，2016，42(6)：87-90.

[4] BI D,，XIE Y，ZHENG Y R.Synthetic aperture radar imaging using basis selection compressed sensing[J].Circuits Systems & Signal Processing,，2015,，34(8)：2561-2576.

[5] LIU X, FAN J, LI W.Concave minimization for sparse solutions of absolute value equations[J].Transactions of Tianjin University，2016,，22(1)：89-94.

[6] 陳發(fā)堂,，丁月友,，馮永帥.大規(guī)模MIMO中基于GSSK系統的稀疏檢測算法[J].電子技術應用，2016,，42(7)：107-110.



作者信息:

段沛沛1,，2，李  輝1,，雒明世2

（1.西北工業(yè)大學 電子信息學院,，陜西 西安710029；2.西安石油大學 計算機學院,，陜西 西安710065）

此內容為AET網站原創(chuàng),，未經授權禁止轉載。