桑坤,，朱向冰,，金慧敏

　　(安徽師范大學(xué) 物理與電子信息學(xué)院，安徽 蕪湖 241000)

       摘要：自整角機(jī)是一種用于角度測量的微型電機(jī),，其輸出包含角度的模擬信號經(jīng)過簡單處理和A/D變換后再通過CORDI算法解碼,。CODIC算法具有精度靈活可調(diào)、運(yùn)算速度快,、硬件實現(xiàn)簡單等優(yōu)點,；通過對CORDC算法角度及對自整角機(jī)輸出信號的象限修正，設(shè)計了一種基于CORDIC算法流水線技術(shù)的自整角機(jī)解碼算法,，并以FPGA為平臺進(jìn)行模擬和仿真,，驗證其準(zhǔn)確性及可行性。

　　關(guān)鍵詞：CORDIC算法,；自整角機(jī),；解碼；FPGA

0引言

　　自整角機(jī)是一種高精度的角度位置傳感器［1］,，廣泛應(yīng)用于航海,、航天、方位同步指示系統(tǒng)火炮等伺服系統(tǒng)中,。自整角機(jī)輸出信號主要以模擬信號進(jìn)行傳送,，減少角度信號在較長距離傳輸時其他信號干擾，同時方便人們控制目標(biāo)元件,。傳統(tǒng)的軸角測量通常采用峰值采樣,、相干解調(diào)或?qū)Ｓ玫妮S角數(shù)字轉(zhuǎn)換芯片實現(xiàn)［2］，但是這幾種算法也存在精度不高,、運(yùn)算速度較慢及價格昂貴等缺點,。本文使用的坐標(biāo)旋轉(zhuǎn)數(shù)字計算（Coordinate Rotation Digital Computer，CORDIC）算法采用迭代的思想,，不進(jìn)行乘法運(yùn)算,，提高了運(yùn)算速度。由于該算法是一種數(shù)字數(shù)字的算法，有線性的收斂域和序列及迭代次數(shù)可有效提高精度［3］,。

　　本文利用CORDIC算法［4］計算反正切函數(shù)并結(jié)合自整角機(jī)輸入輸出信號的特點,，實現(xiàn)一種運(yùn)算速度高、可靠性好,、精度高,、硬件設(shè)計簡單的角度解碼，并用FPGA豐富硬件資源簡化程序,，提高電路的運(yùn)算速度和可靠性,。

1自整角機(jī)基本原理

　　自整角機(jī)是利用自整步特性將轉(zhuǎn)角變?yōu)榻涣麟妷夯蛴山涣麟妷鹤優(yōu)檗D(zhuǎn)角的感應(yīng)式微型電機(jī)，當(dāng)激勵繞組以一定的頻率交流電壓勵磁時,，輸出繞組的電壓幅值與轉(zhuǎn)子轉(zhuǎn)角成正余弦函數(shù)關(guān)系［5］,。在結(jié)構(gòu)上，自整角機(jī)主要由轉(zhuǎn)子和定子組成,，轉(zhuǎn)子軸上的單相繞組通過電刷和滑環(huán)與外界連接,，引出端用Z1和Z2表示；定子的三相對稱繞組以Y型連接,，空間位置上依次落后120°,，如圖1所示。

　　設(shè)轉(zhuǎn)子轉(zhuǎn)動θ,，自整角機(jī)三路輸出模擬信號,，但是需要電壓激勵。激勵電壓為：

　　S1,、S2,、S3三路定子的感應(yīng)電動勢分別為：

　　上式中sinωt為交流信號，θ是自整角機(jī)偏轉(zhuǎn)的角度,。

2CORDIC算法原理

　　CORDIC算法基本思想是迭代,，通過多個固定的及與運(yùn)算有關(guān)的角度逐次遞減，從而逐漸逼近需要的角度,。

　　CORDIC算法的基本公式在一些文獻(xiàn)中有詳細(xì)推導(dǎo),，這里僅作簡要的說明。

　　如圖2所示,，假設(shè)向量(xi,yi)按照一定角度旋轉(zhuǎn)到(xj,yj)則有：

　　起始位置到終點位置可以通過多步迭代旋轉(zhuǎn)過程實現(xiàn),，每一步旋轉(zhuǎn)一定的相位，則：

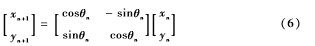
　　提取cosθn,，則有：

　　定義每一步的旋轉(zhuǎn)角度為θn=arctan(12n),，總的旋轉(zhuǎn)相位為θ=∑Snθn，其中Sn=±1,，則:

　　其中K為增益因子,，其值的變化取決于迭代次數(shù),，當(dāng)?shù)螖?shù)N很大時：

　　CORDIC算法有旋轉(zhuǎn)模式（rotation）和矢量模式（vectoring）兩種旋轉(zhuǎn)模式［6］，該解碼算法采用矢量模式,。迭代方程如下：

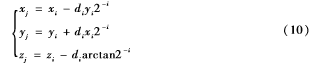
　　其中zj是角度累加器,，di=－sgn(yi)=1,y<0（順時針旋轉(zhuǎn)）

　　－1,y>0（逆時針旋轉(zhuǎn)）,。

　　假設(shè)初始條件為x0=x,y0=y,z0=0,經(jīng)過n次迭代后,矢量模式的表達(dá)式為：

3自整角機(jī)解碼算法設(shè)計

　　3.1自整角機(jī)輸出信號的象限修正

　　利用CORDIC算法計算反正切值［7］,，由于arctan2－i(0≤i≤n)所能計算的值區(qū)域為－π2，π2,，要計算全角度時必須對角度進(jìn)行預(yù)處理,。將公式（2）-（4）整理得：

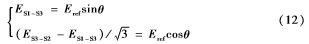
　　對自整角機(jī)三路輸出的模擬信號進(jìn)行簡單運(yùn)算，得到只含角度θ的正余弦值和正切值,；然后對得到的正余弦函數(shù)進(jìn)行修正,，得到角度θ所在的范圍,。

　　將得到的正弦和余弦函數(shù)進(jìn)行區(qū)間范圍的判斷,，sinθ和cosθ所在的區(qū)間范圍如下：當(dāng)|cosθ|－|sinθ|≥0,θ在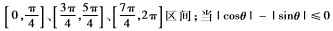

定義一個中間變量α，則有：

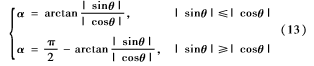
　　sinθ,、cosθ在不同區(qū)域的值如表1所示,。

上述輸出角度θ的劃分修正，將角量全部轉(zhuǎn)換到0,，π4,，可有效避免討論sinθ或cosθ等于0的情況，在計算過程中,，也避免了反正切函數(shù)在±π2和±π附近角度不收斂無法計算的情況,，因此不占用和浪費(fèi)大量資源，提高了運(yùn)算速度,。

　　3.2CORDIC求全角量反正切

　　對于自整角機(jī)輸出信號,，在旋轉(zhuǎn)的角度一定時，可將輸出的信號理解為勵磁信號Eref=ERLO－RHIsinωt對sinθ和cosθ進(jìn)行的幅度調(diào)制［6］,，而勵磁信號的變化只是幅值發(fā)生變化,，對自整角機(jī)輸出信號的正確解碼不產(chǎn)生影響，只要能正確地解碼出角度值,，則幅值的變化可以忽略不計,，本文選擇CORDIC算法的矢量模式，令Uxin=cosθ,Uyin=sinθ,z0=0,，經(jīng)過n次迭代后得到式（11),。

　　3.3CORDIC算法的角度輸出

　　自整角機(jī)解碼算法采用20位二進(jìn)制數(shù)表示輸出信號，輸入信號為16位二進(jìn)制數(shù),。1°=216360≈18210=101101102,；arctan(2－n)可表示為2202π·arctan(2－n),，當(dāng)?shù)螖?shù)n不少于16時，就能夠達(dá)到一定的精度,。

4CORDIC自整角機(jī)解碼算法的實現(xiàn)及仿真

　　4.1CORDIC自整角機(jī)解碼算法的實現(xiàn)

　　基于CORDIC算法實現(xiàn)的設(shè)計有迭代結(jié)構(gòu)和流水線結(jié)構(gòu)［7］,，流水線結(jié)構(gòu)運(yùn)算速度比迭代結(jié)構(gòu)快，采用流水線結(jié)構(gòu)可有效提高算法速度,。在流水線結(jié)構(gòu)中,，旋轉(zhuǎn)角度集的各個值均是直接聯(lián)到累加器的［6］ 。流水線結(jié)構(gòu)如圖3所示,。

　　4.2FPGA實驗仿真

　　采用VHDL語言描述并在FPGA上實現(xiàn)流水線結(jié)構(gòu)的CORDIC解碼算法,，利用QuartuesII進(jìn)行仿真，驗證其可行性與正確性,。

　　設(shè)定系統(tǒng)時鐘為98 MHz,輸入一位時鐘信號clk,1位使能信號ena,，16位輸入信號Xin、Yin,，及20位角度解碼信號輸出Aout,，仿真選取50°和260°進(jìn)行模擬，驗證該解碼算法的正確性,。

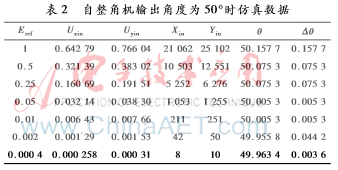
　　當(dāng)自整角機(jī)的角度為50°時,，QuartuesII仿真圖及仿真數(shù)據(jù)如圖4和表2所示。

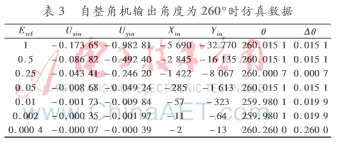
　　當(dāng)自整角機(jī)的角度為260°時,，仿真圖及仿真數(shù)據(jù)如圖5和表3所示,。

　　由上述數(shù)據(jù)可知，在角度一定,、Eref變化的情況下,，該算法可以正確地解碼θ，并且達(dá)到一定的精度,；仿真中的冒險競爭不是發(fā)生在時鐘上升沿,，不影響角度的正確解碼。從仿真圖上可以看出有一定的延時,，這是由迭代運(yùn)算造成的效果,，可以通過改變時鐘頻率進(jìn)行改善。

5結(jié)論

　　本文采用CORDIC算法在FPGA上實現(xiàn)自整角機(jī)輸出角度的解碼,，并對自整角機(jī)的輸出信號進(jìn)行簡單的運(yùn)算和角度的象限修正預(yù)處理,，在可計算的范圍內(nèi)，通過QuartuesII驗證其可行性與正確性,，提升了運(yùn)行速度和精度,，從而驗證了該設(shè)計的正確可行。

　　參考文獻(xiàn)

　?。?］ 楊桂華. 高精度自整角機(jī)精度的分析［J］. 微電機(jī),1990（1）:11-15.

　?。?］ 李全.正交三角函數(shù)的CORDIC實現(xiàn)［J］.微計算機(jī)信息,2008,24(12-3):268-269.

　?。?］ 陳石平，廖丁毅,，張權(quán).CORDIC算法在正角調(diào)制技術(shù)的應(yīng)用［J］.廣西通信技術(shù),，2015（2）：49-52.

　　［4］王華華,陳雷成,陳發(fā)堂,，等.基于FPGA的STACORDIC算法在SCME中的應(yīng)用［J］.電子技術(shù)應(yīng)用,2014,40(8):109-111,115.

　?。?］ ANDRAKA R. A survey of CORDIC algorithms for FPGA based computers［M］. New York: ACM Press, 1998.

　　［6］ VOLDER E. The CORDIC trigonometric computing technique［J］.IRE Transactions on Electronic Computers,1959, 8:379-385.

　?。?］ 李滔,韓月秋.基于流水線CORDIC 算法的三角函數(shù)發(fā)生器［J］.電子技術(shù)應(yīng)用, 2000, 25(4):85-87.