摘  要： 針對半色調(diào)圖像分類中只存在0和1的特點(diǎn),，提出了一種基于改進(jìn)的協(xié)方差矩陣在半色調(diào)圖像中的分類方法。根據(jù)協(xié)方差矩陣在實(shí)現(xiàn)半色調(diào)圖像分類中個(gè)數(shù)少且并未體現(xiàn)其局部和全局信息的特性,，對協(xié)方差矩陣的底層特征進(jìn)行改進(jìn),。利用樣本的局部特性和核密度估計(jì)方法，實(shí)現(xiàn)黎曼流形上的貝葉斯分類策略,。實(shí)驗(yàn)中研究協(xié)方差矩陣的底層特征與傳統(tǒng)協(xié)方差矩陣的特征提取方法并對其進(jìn)行分類性能比較,。實(shí)驗(yàn)結(jié)果表明，在半色調(diào)圖像分類中,，與傳統(tǒng)的協(xié)方差矩陣相比較,，改進(jìn)的協(xié)方差矩陣提取出的特征在分類中平均錯(cuò)誤分類率更低。

　　關(guān)鍵詞： 半色調(diào)圖像,；協(xié)方差矩陣,；黎曼流形；最近鄰分類器

0 引言

　　數(shù)字半色調(diào)（也稱為空間抖動(dòng)）始于19世紀(jì)50年代,，是將一幅連續(xù)色調(diào)的圖像先進(jìn)行二值化處理，再用這些黑白二色的點(diǎn)來表示各個(gè)等級灰度的技術(shù)[1],。數(shù)字半色調(diào)技術(shù)已廣泛應(yīng)用于傳真,、打印、印刷,、顯示設(shè)備及數(shù)字圖像的壓縮存儲(chǔ)等領(lǐng)域,。較常用的數(shù)字半色調(diào)方法有：有序抖動(dòng)法[2]、誤差分散法[3],、點(diǎn)分散法[4],、綠噪聲半調(diào)法[5]等。通過分析現(xiàn)有的半色調(diào)技術(shù)可知,，不同半色調(diào)技術(shù)應(yīng)用于多級圖像時(shí)將產(chǎn)生具有各自不同特性的半色調(diào)圖像[6],，有周期性、點(diǎn)分布,、點(diǎn)分散性,、點(diǎn)相關(guān)性等,。當(dāng)通用型逆半色調(diào)技術(shù)用于某種半色調(diào)圖像的重建時(shí)，將缺少相關(guān)半色調(diào)模式信息,，所以較難獲得半色調(diào)圖像的最優(yōu)重建,。

　　目前數(shù)字半色調(diào)圖像分類方法的研究比較少。Chang[7]首先對半色調(diào)圖像分類進(jìn)行研究,，指出在半色調(diào)圖像恢復(fù)成連續(xù)灰度圖像之前運(yùn)用一維自相關(guān)函數(shù),，提取出四類半色調(diào)圖像，最后用BP神經(jīng)網(wǎng)絡(luò)進(jìn)行分類,。雖然該方法分類結(jié)果有時(shí)能達(dá)到100%,，但獲取的類別比較少。文志強(qiáng)[1,，8]提出一種在3個(gè)方向上利用像素自相關(guān)特征進(jìn)行同或運(yùn)算來描述紋理特征的有監(jiān)督流形上的半色調(diào)分類方法,，利用圖像分塊的思想獲取紋理特征，目的在于提高建模效率和紋理特征的有效性,。

　　以上方法都基于歐式空間,，本文提出的方法需在黎曼空間上進(jìn)行特征匹配，再利用黎曼距離和局部概率密度來實(shí)現(xiàn)對半色調(diào)圖像的分類,。黎曼流形是具有黎曼度量的微分流形,，即有一個(gè)對稱正定協(xié)變的二階張量場在這個(gè)流形上，相比于歐式空間,，具有更豐富的黎曼度量方法,，是研究概率分布和模式匹配的有效工具。

1 傳統(tǒng)協(xié)方差矩陣建模方法

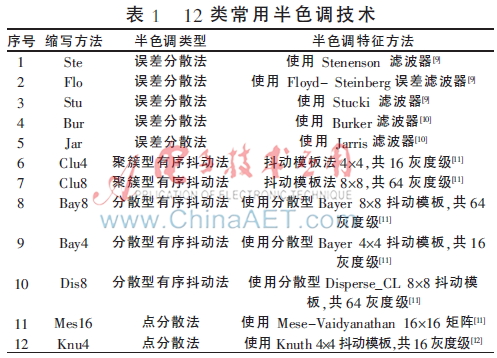
　　通過多種半色調(diào)技術(shù)可將多級灰度圖像轉(zhuǎn)化為半色調(diào)圖像樣本,，并對其進(jìn)行分類,。12種常用半色調(diào)技術(shù)，如表1所示,。圖1給出相應(yīng)的12幅灰度圖像產(chǎn)生的半色調(diào)圖像（以lena（大?。?56×256）為例）。由圖1可知,，不同半色調(diào)技術(shù)產(chǎn)生的半色調(diào)圖像具有不同的紋理特征,。一些半色調(diào)圖像紋理比較明顯，如圖1中的（a）,、（g）,、（h）、（i）子圖,；另一些紋理差別不明顯,，分類較困難，如圖1中（b）、（c）,、（e）和（l）子圖難以區(qū)分,，子圖（d）、（f）,、（j）和（k）區(qū)別也較小,。由分析可知，造成半色調(diào)圖像分類錯(cuò)誤率高的最主要原因是紋理差別不明顯,。因此,，本文在半色調(diào)圖像上對協(xié)方差矩陣改進(jìn)之后再進(jìn)行構(gòu)建與分類。

　　協(xié)方差矩陣[13-14]（Covariance matrix,，COV）是概率論,、統(tǒng)計(jì)學(xué)的一個(gè)概念，通過不同維度計(jì)算協(xié)方差構(gòu)成的矩陣,，衡量兩個(gè)隨機(jī)變量的變化,。協(xié)方差矩陣表示一個(gè)多維隨機(jī)變量各個(gè)維度之間的相關(guān)性。協(xié)方差矩陣于2006年被Tuzel O,，Porikli F[15]作為描述子最先應(yīng)用在醫(yī)學(xué)圖像處理的目標(biāo)檢測中,，能夠很好地描述圖像，因?yàn)閷⑵溆糜趫D像特征提取時(shí),，將區(qū)域圖像不同的特征值通過統(tǒng)計(jì)矢量的方式統(tǒng)一于協(xié)方差矩陣中,。COV作為描述子具有很好的魯棒性，對外部形態(tài)和光照的改變能很好地維持其主要特征的不變性,，所以可將COV應(yīng)用于半色調(diào)圖像的特征提取中[16],。

　　COV定義如下：

　　設(shè)I為一維強(qiáng)度或三維強(qiáng)度的彩色圖像，f為原圖I內(nèi)具有M×N個(gè)像素的區(qū)域圖像,，h為該區(qū)域f內(nèi)提取的d維特征向量,，如式（1）所示：

　　將區(qū)域f每個(gè)像素的特征向量通過共生關(guān)系統(tǒng)一到協(xié)方差矩陣C中，如式（2）所示：

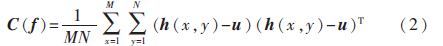
　　其中,，h（x,，y）為區(qū)域矩陣每個(gè)元素的特征向量，u為M×N個(gè)dx1維特征向量h（x,，y）的均值,，h（x,，y）表示區(qū)域圖像每個(gè)像素的底層特征,，如式（3）所示：

　　h（x，y）=[|fxx|,，|fyy|,，|fx|，|fy|，f（x,，y）]T（3）

　　式（2）中C（f）為協(xié)方差矩陣,，融合了原始圖像底層的五個(gè)特征，等價(jià)于公式（4）：

　　C（f）=HHT（4）

　　由公式（1）~（4）可知,，COV能夠較好地表示圖像的特征,，且具有如下優(yōu)點(diǎn)：

　　（1）很好的辨識度,。能夠?qū)^(qū)域圖像多種特征融合于COV中,。

　　（2）更低的維數(shù),。COV是一個(gè)對稱的半正定矩陣,，所以d維的特征向量構(gòu)成的協(xié)方差矩陣具有（d2+d）/2個(gè)不同值。

　?。?）很好的魯棒性,。將一幅圖像旋轉(zhuǎn)后，若選取的特征適當(dāng),，則形成的COV不發(fā)生相應(yīng)的改變,。

　　2 改進(jìn)的協(xié)方差矩陣建模方法

　　COV雖然有很多優(yōu)點(diǎn)，但也存在不足,。由公式（2）可知,，當(dāng)h（x，y）=u時(shí),，協(xié)方差矩陣的行列式有可能為0,，所以準(zhǔn)確地講，協(xié)方差矩陣應(yīng)屬半正定矩陣,，針對該問題可采用附加一個(gè)足夠小的對角矩陣p來進(jìn)行預(yù)處理,。

　　可以看到，圖1中12幅半色調(diào)圖像的紋理不明顯,，分類較困難,。針對這一難點(diǎn)，可將半色調(diào)圖像求梯度,，即通過梯度信息來描述圖像中物體的邊緣,、輪廓、形狀等紋理特征,。對圖像加入水平邊緣算子[-1,，0，1]和垂直邊緣算子[-1,，0,，1]T，并將該特征加入?yún)f(xié)方差矩陣的底層特征中。所以提出改進(jìn)的協(xié)方差矩陣（Improved covariance matrix,，ICM）,。

　　本文獲取區(qū)域半色調(diào)圖像f的底層特征如公式（5）所示，通過公式（2）將其構(gòu)成COV,。

　　h（x,，y）=[x，y,，|fx|,，|fxx|，|fy|,，|fyy|,，f（x，y）,，

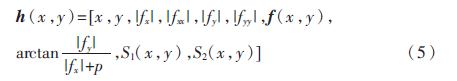
　　其中,，x，y分別為區(qū)域半色調(diào)圖像的坐標(biāo)值,，f（x,，y）設(shè)定以位置（x，y）為中心的n×n（實(shí)驗(yàn)中n取9）鄰域各個(gè)像素值之和,，|fx|,、|fxx|為像素值在x方向的一階、二階導(dǎo),，|fy|,、|fyy|為像素值在y方向的一階、二階導(dǎo),。arctan|fy|/（|fx|+p）為f（x,，y）在位置（x，y）處的梯度,。由于協(xié)方差矩陣的行列式有可能為0,，所以添加一個(gè)無窮小量。S1（x,，y）=（|Ix|*|Ix|+|Iy|*|Iy|+|fx|*|fx|+|fy|*|fy|）,，其中Ix為水平邊緣梯度，Iy為垂直邊緣梯度,。S2（x,，y）=arctan|Iy|/（|Ix|+p）。圖2為對應(yīng)圖1中ICM特征圖像示例圖,。由圖2可知,，各矩陣的特征圖都有一定的差別，這說明提取的特征矩陣可用于描述半色調(diào)圖像,。即加入梯度算子后,，圖像的輪廓明顯變得更清晰。將梯度算子加入COV的底層特征后,，特征更明顯,，更容易區(qū)分圖像的紋理信息。ICM算法實(shí)現(xiàn)步驟如下：

　　算法：ICM算子的構(gòu)造

　　輸入：一幅大小為M×N的區(qū)域半色調(diào)圖像f

　　輸出：能夠表征原始半色調(diào)圖像的改進(jìn)協(xié)方差矩陣

　　Step1 根據(jù)公式（5）獲取區(qū)域半色調(diào)圖像的十個(gè)底層特征,，分別是x,，y，|fx|,，|fxx|,，|fy|，|fyy|,，f（x,，y），arctan|fy|/（|fx|+p）,，S1（x,，y），S2（x,，y）,；

　　Step2根據(jù)公式（2）計(jì)算區(qū)域半色調(diào)圖像f的協(xié)方差 矩陣C（f）。

3 實(shí)驗(yàn)結(jié)果及比較

　　3.1 實(shí)驗(yàn)環(huán)境

　　本實(shí)驗(yàn)在Windows 7操作系統(tǒng)環(huán)境下進(jìn)行,，采用VC6.0結(jié)合OpenCV 1.0及MATLAB 7.11進(jìn)行編程,。常用半色調(diào)圖像由VC6.0結(jié)合OpenCV 1.0產(chǎn)生，ICM特征的提取使用MATLAB 7.11生成,。

　　3.2 實(shí)驗(yàn)結(jié)果

　　對原始圖像產(chǎn)生12類常用半色調(diào)圖像庫,，對每類隨機(jī)取出410幅樣本（大小為256×256）。對每幅圖像提取ICM特征,，之后從每類410個(gè)協(xié)方差矩陣的特征中隨機(jī)抽取205個(gè)作為訓(xùn)練樣本,，剩余205個(gè)作為測試樣本。為驗(yàn)證提出方法的有效性,，取相同K值不同類型的特征矩陣在黎曼流形上采用K最近鄰分類器對紋理特征進(jìn)行分類?，F(xiàn)取K=23，應(yīng)用傳統(tǒng)的協(xié)方差矩陣與本文提出方法對隨機(jī)取出的410×12幅圖像進(jìn)行分類,，比較其分類精度如表2和表3所示,。

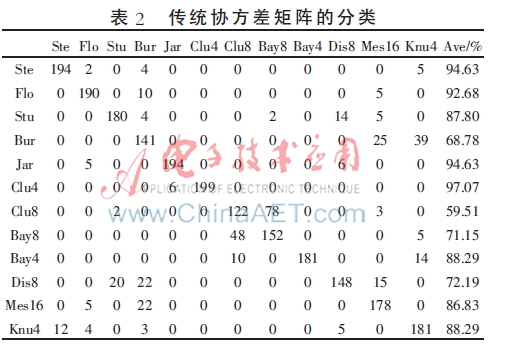
　　由表2可知，采用傳統(tǒng)協(xié)方差矩陣對12類常用的半色調(diào)圖像的平均分類正確率為83.487 5%,，由表3可知,，提出方法對12類常用半色調(diào)圖像的平均分類正確率為92.598 3%,。比較表明，本文所提出的方法有所改善,。

　　3.3 參數(shù)影響

　　對于多類別（類別數(shù)大于2）投票時(shí)可能會(huì)出現(xiàn)兩種或多種類別票數(shù)相同問題,，這種情況下分類器取K個(gè)近鄰值中最小值對應(yīng)的類別為最終類別。分類結(jié)果性能采用平均分類錯(cuò)誤率（公式（7））和分類錯(cuò)誤方差率（公式（8））來評價(jià),，其中公式（6）為錯(cuò)誤分類率,。平均分類錯(cuò)誤率越小說明分類效果越好，分類錯(cuò)誤方差率越小說明分類器越穩(wěn)定,。

　　其中,，nj為測試樣本總數(shù)，mj為正確分類樣本數(shù),，N為總的類別數(shù)（N=12）,，j為類別數(shù)，j=1,，2,，…，12,。

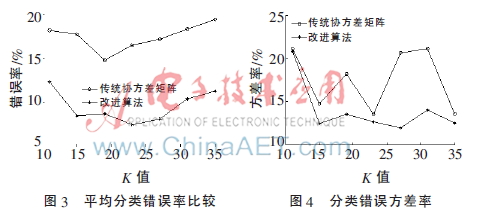
　　本實(shí)驗(yàn)測試不同K值對相同類型的影響,。由12類常用半色調(diào)圖像變更不同的K值，分別取11,，15,，19，23,，27,，31，35七個(gè)值來比較傳統(tǒng)協(xié)方差矩陣和提出方法提取特征矩陣對其進(jìn)行eave和v比較,，折線圖比較如圖3和圖4所示,。由圖3可知，常用12類半色調(diào)圖像的分類中,，COV在K=19時(shí)分類效果最好,，ICM在K=23時(shí)分類效果最好。但不管K為何值,，提出方法效果均優(yōu)于COV,。由圖4的v折線圖可知，COV在K=23時(shí)分類器最穩(wěn)定,，ICM在K=27時(shí)v最小,，此時(shí)的分類器性能最穩(wěn)定。不管K為何值,，本文提出方法的分類器更穩(wěn)定,。由此證明,，提出方法的有效性。

4 總結(jié)

　　針對12類常用半色調(diào)圖像的分類問題,，對半色調(diào)圖像的特征建模和分類方法進(jìn)行了深入研究,，提出對傳統(tǒng)的協(xié)方差矩陣進(jìn)行改進(jìn)，并用黎曼流形上的K最近鄰方法對提取出的特征矩陣進(jìn)行分類,。通過比較分類精度來驗(yàn)證提出方法的有效性。實(shí)驗(yàn)證明,，將傳統(tǒng)的協(xié)方差矩陣與提出方法進(jìn)行eave和v比較,，可知提出方法在K=23時(shí)，eave最低,，即分類效果最好,；在K=27時(shí)，v最小,，即分類器性能最穩(wěn)定,，所以在選擇K值時(shí)應(yīng)視需求而定。

參考文獻(xiàn)

　　[1] 文志強(qiáng),，胡永祥,，朱文球.基于統(tǒng)計(jì)量模板的半色調(diào)圖像特征提取與分類[J].計(jì)算機(jī)科學(xué)，2013,，40（12）：94-112.

　　[2] LIU Y F,， GUO J M. New class tiling design for dot-diffused halftoning[J]. IEEE Trans. on Image Process， 2013,，2（3）： 1199-1208.

　　[3] STEVENSON R. Inverse halftoning via MAP estimation[J].IEEE Trans. on Image Processing,， 1997， 6（4）： 574-583.

　　[4] MESE M,， VAIDYANATHAN P P. Recent advances in digital halftoning and inverse halftoning methods[J]. IEEE Trans. on Ciruits and Systems： Fundamental Theory and Applications,， 2002，49（6）： 790-805.

　　[5] LIU Y F,， GUO J M,， LEE J D. Inverse halftoning based on the Bayesian theorem[J]. IEEE Trans. on Image Process， 2011,， 20（4）： 1077-1084.

　　[6] 文志強(qiáng),，胡永祥，朱文球.黎曼流形上半調(diào)圖像的協(xié)方差建模與貝葉斯分類方法[J].模式識別與人工智能,，2013,，26（11）：993-1003.

　　[7] CHANG P C， YU C S. Neural net classification and LMS reconstruction to halftone images[C]. Proc. of the SPIE Visual Communications and Image Processing,， San Jose,， USA,， 1998： 592-602.

　　[8] Wen Zhiqiang， Hu Yongxiang,， Zhu Wenqiu. A novel classification method of halftone image via statistics matrices[J]. IEEE Trans. on Image Process,， 2014， 23（11）： 4724-4736.

　　[9] GUO J M,， LIU Y F,， CHANG J Y， et al. Efficient halftoning based on multiple look-up tables[J]. IEEE Trans. on Image Process,， 2013,， 22（11）：4522-4531.

　　[10] MESE M， VAIDYANATHAN P P． Recent advances in digital halftoning and inverse halftoning methods[J]. Circuits and Systems I： Fundamental Theory and Applications,， IEEE Transactions on,， 2002，49（6）：790-805.

　　[11] ULICHNEY R. Digital halftoning and the physical reconstruction function[C]. Ph. D Dissertation. Cambridge,， USA： Massachusetts Institute of Technology,， 1986.

　　[12] KNUTH D E. Digital halftones by dot diffusion[J]. ACM Trans. on Graphics， 1987,， 6（4）：245-273.

　　[13] MESE M,， VAIDYANATHAN P P. Optimized halftoning using dot diffusion and methods for inverse halftoning[J]. IEEE Trans. on Images Process， 2000,，9（4）：691-709.

　　[14] WU Y,， CHENG J， WANG J,， et al. Real-time probabilistic covariance tracking with efficient model update[J]. IEEE Trans. on Image Process,， 2012，21（5）：2824-2837 .

　　[15] PORIKLI F,， TUZEL O,， MEER P. Covariance tracking using model update based on lie algebra[C]. Computer Vision and Pattern Recognition， 2006 IEEE Computer Society Conference on. IEEE,， 2006：728-735.

　　[16] Wen Zhiqiang,， Hu Yongxiang， Zhu Wenqiu. Bayesian classification of halftone image based on region covariance[J]. Intelligent System Design and Engineering Applications,， 2013（3）：398-401.