LTE所選擇的上行傳輸方案是一個新變量：SC-FDMA(單載波-頻分多址)相比于傳統(tǒng)OFDMA其優(yōu)點是既有單載波的低峰均功率比(PAPR)，又有多載波的可靠性,。在上行鏈路這點特別重要,，較低的PAPR可在傳輸功效方面極大提高移動終端的性能,，因此可延長電池使用壽命。代表LTE物理上行共享信道(PUSCH)的基帶信號產(chǎn)生過程如圖1所示[1],。

    圖1中的轉(zhuǎn)換預編碼是由一種對稱形式DFT完成,，其種類及變換長度L=2k1×3k2×5k3(L≤1 200)見表1。

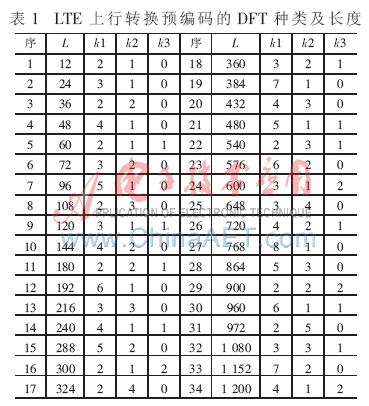
    轉(zhuǎn)換預編碼是根據(jù)不同的輸入長度L動態(tài)地執(zhí)行表1中的一種DFT,。其主要特點是包含的DFT種類多,、規(guī)模龐大，這給硬件設計帶來挑戰(zhàn),。以前的文獻大都以基2或單個混合基FFT[6]為重點進行闡述,，而以多種混合基FFT為核心的文章還很難發(fā)現(xiàn)。本文提出一種基于FPGA的轉(zhuǎn)換預編碼解決方案,。
1 算法選擇
    Cooley-Tukey算法和Good-Thomas算法是當前流行的FFT算法,，文獻[2]中已對其原理進行過深入討論，這里不再贅述,。
    (1)Cooley-Tukey算法具有良好的模塊性,，并且可以實現(xiàn)原位計算，對輸入數(shù)據(jù)以及旋轉(zhuǎn)因子的抽取具有規(guī)律性,。文獻[3]提出的一種基3 FFT算法是Cooley-Tukey算法應用在基3 FFT中的另一種表述,。這一算法區(qū)別于其他FFT算法的一個重要事實就是因子可以任意選取，通用性強,，且所有的運算單元均相同,，易于實現(xiàn)。
    (2)Good-Thomas算法只適合因子互質(zhì)的情況,，由于避免了中間級乘旋轉(zhuǎn)因子的運算,，因此比Cooley-Tukey算法的運算次數(shù)少得多。FFT點數(shù)越大,，越能體現(xiàn)其在節(jié)省資源方面的優(yōu)點,。
    文獻[4]提出一種基于Cooley-Tukey算法的傳輸預編碼解決方案。此方案的優(yōu)點是操作簡單,、模塊規(guī)則,、利于編程實現(xiàn)；缺點是需要做的級間旋轉(zhuǎn)因子乘法較多(最多達幾百),，乘法器和存儲器等硬件資源開銷較大,，同時將大大增加系數(shù)初始化的工作量。對幾種不同長度FFT運算量進行比較見表2,。

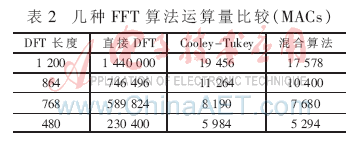
    表2中的混合算法指Good-Thomas算法與Cooley-Tukey算法相結(jié)合,。可以看出,，Good-Thomas算法與Cooley-Tukey算法相結(jié)合與文獻[4]相比,，減少了級間旋轉(zhuǎn)因子乘法數(shù),，可以有效降低運算量，這些運算量的降低對整個系統(tǒng)的實現(xiàn)起著至關重要的作用,，而其付出的代價只是復雜度的略微提升,。
    綜上所述，在實現(xiàn)混合FFT時,，選擇Good-Thomas算法與Cooley-Tukey算法相結(jié)合,，且優(yōu)先選擇Good-Thomas算法，其次為Cooley-Tukey算法,，系統(tǒng)設計將從Good-Thomas算法出發(fā),。
2 總體結(jié)構(gòu)設計
    從表1中看出，LTE上行轉(zhuǎn)換預編碼要進行的FFT變換種類多,，但每一種變換的架構(gòu)是相似的，都是由基2及非基2點FFT的公共模塊組成,?；?有點數(shù)為4，8,，16,，32，64,，128,，256的模塊，非基2的有點數(shù)為3,，9,，15，27,，45,，75，81,，135,，225和243的模塊，只要抽出這些公共模塊并精心設計,，再合理地調(diào)用,，就會順利完成這個看似繁瑣的工作。
    圖2所示總體結(jié)構(gòu)框圖中,，模塊A和C分別為數(shù)據(jù)輸入和輸出模塊,；模塊B為數(shù)據(jù)處理模塊，其主要思想是動態(tài)配置和公共模塊的復用,，內(nèi)部FFT模塊事先單獨生成,，MUX1,，MUX2是選擇器，在不同輸入點數(shù)的情況下動態(tài)配置不同的內(nèi)部FFT模塊來組合成外層FFT,，這樣內(nèi)部FFT模塊就可以達到復用的目的,，可以大大減少總體資源耗用，而處理速度也與單獨執(zhí)行各FFT相當,。

3 硬件實現(xiàn)
    在實際應用中,，一般由FPGA完成需要快速和較為固定的運算，由DSP完成靈活多變和運算量較大的任務[7],。Xilinx Virtex-5 SXT平臺針對具有低功耗串行連接功能的DSP和存儲器密集型應用進行了優(yōu)化,，具有硬件結(jié)構(gòu)可重構(gòu)的特點，適合算法結(jié)構(gòu)固定,、運算量大的前端數(shù)字信號處理,，可以大量卸載這些功能，釋放DSP帶寬以處理其他功能,，所有這一切都使得FPGA在數(shù)字信號處理領域顯示出自己特有的優(yōu)勢,。
3.1 地址映射
    以1 080點FFT在圖2所示系統(tǒng)中的實現(xiàn)過程分析系統(tǒng)工作原理。因為1 080=8×135,，且8和135互質(zhì),，故外層采用Good-Thomas算法。
    輸入地址映射：
  
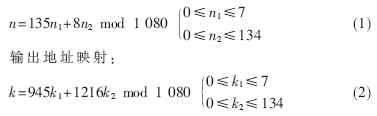
    FPGA內(nèi)嵌Block RAM的使用可以大大節(jié)省FPGA的可配置邏輯功能塊（CLB）資源,。Good-Thomas算法需要對輸入輸出數(shù)據(jù)進行排序,，輸入輸出端處理方法相同，這里只介紹輸入端處理,。在輸入端,，鑒于Block RAM的特征，設置一個ROM和RAM,，如圖2模塊A所示,。對于不同長度的FFT，ROM不同,，但RAM可以共用,。在ROM里預先存放輸入數(shù)據(jù)在RAM1中的位置序號，此位置序號由（1）式得到,，在時鐘沿到來時,，先順序讀出存儲在ROM中的位置序號，將此數(shù)作為RAM1的地址輸入,，就能將輸入數(shù)據(jù)存放到RAM1中的不同位置,。這樣在輸入數(shù)據(jù)的同時完成了數(shù)據(jù)的排序，一舉兩得,。1 080點FFT的輸入和輸出端地址索引如圖2所示,，其邏輯時序圖見圖3,。圖3中，RAM_in由測試數(shù)據(jù)xn_i和xn_r進行位拼接后輸入,。

3.2 內(nèi)部FFT處理單元
    當進行圖2模塊B中的操作時,，內(nèi)部FFT模塊先單獨生成。Xilinx提供的FFT IP核適用于基2點的FFT變換,，其所采用的算法為Cooley-Tukey算法,，變換長度為N=pow2(m)，m=3~16,，數(shù)據(jù)采樣精度和旋轉(zhuǎn)因子精度都為8~24,，故模塊B的8、16,、32,、64、128及256點FFT都可用IP核生成,。選擇“Pipelined,streaming I/O”生成基2點FFT模塊,，可以減少整體處理時間。15,、45、75,、135,、225點FFT模塊的外層算法是Good-Thomas算法，其余采用Cooley-Tukey算法實現(xiàn),。
    具體到1 080點FFT,，將RAM1中的數(shù)據(jù)順序讀出，由MUX1選擇進行8點FFT變換,，完成第一級操作后,，所得中間結(jié)果順序存儲在RAM2中；然后再將RAM2中的中間結(jié)果取出,，由MUX2選擇進行135點FFT變換,，共操作8次，完成第二級操作,，所得結(jié)果按模塊C中ROM指示的順序存儲在RAM1中,；最后順序輸出RAM1中的內(nèi)容就是1 080點FFT的結(jié)果。
3.3 乘法器設計
    量化效應在數(shù)字信號處理技術實現(xiàn)時是很重要的問題,，主要包括運算量化效應,、系數(shù)量化效應等，前者的影響大于后者[5],。運算中還可能出現(xiàn)溢出,，造成更大的誤差,。上述問題對乘法器的設計提出了要求，由上文知,，基2 FFT由IP核生成,，故此處的乘法器設計只針對非基2 FFT有效。
    Xilinx的XC5VSX95T內(nèi)部共有640個DSP48E,，每個DSP48E包含一個25×18 乘法器,。在調(diào)用乘法器IP時，將乘數(shù)設為寬度為25和18的signed型（旋轉(zhuǎn)因子位寬為18）,，輸出截取結(jié)果的[41：17]共25 bit,，乘法器輸入輸出寬度相等，在結(jié)果輸出的同時對結(jié)果進行縮放,，這樣利于程序模塊化,，但前提是要保證數(shù)據(jù)不溢出。由于輸入采樣數(shù)據(jù)寬度只有16 bit,，而轉(zhuǎn)換預編碼輸入數(shù)據(jù)最大長度只有1 200點,，再考慮旋轉(zhuǎn)因子系數(shù)小于1，可以斷定25 bit位寬可使乘法器結(jié)果不溢出,，且運算精度也可滿足要求,。
4 性能分析
    程序利用Verilog HDL硬件描述語言編寫，在Xilinx公司的高性能設計開發(fā)工具ISE10.1i中編譯成功,。當FPGA芯片選為XC5VSX95T時,，在Synplify Pro 9.6.1中進行邏輯優(yōu)化與綜合后顯示其最大時鐘頻率為105.6 MHz，F(xiàn)Fs耗用29 150/58 880,，LUTs耗用37 625/58 880,，乘法器耗用414/640，Block Ram耗用176/488,，各項指標都合符要求,。布局布線成功后，在Matlab中產(chǎn)生一實正弦測試信號,，經(jīng)采樣量化成1 200點數(shù)據(jù)后輸入Modelsim SE 6.1d對程序進行后仿真,，然后輸出結(jié)果回送至Matlab，得到仿真圖如圖4,。

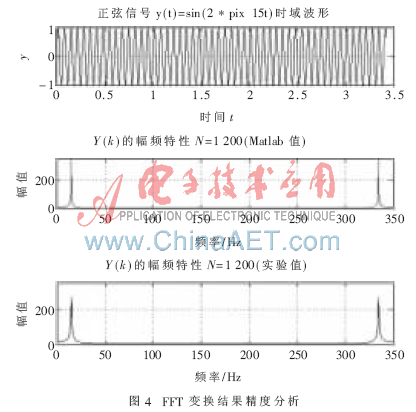
    由圖4可以看出FFT處理器處理后的結(jié)果和Matlab計算的理論結(jié)果基本一致,，都在頻率為15 Hz和335 Hz處取得最大FFT絕對值，兩者之間的誤差正是數(shù)字信號處理量化效應的體現(xiàn),。從整體看,，這些誤差是數(shù)據(jù)在經(jīng)過采樣量化和截斷處理后不可避免的且是可以容忍的，因此可以判斷測試結(jié)果符合精度指標。
    本文討論了應用在LTE上行轉(zhuǎn)換預編碼中的多種FFT的軟硬件實現(xiàn),。與各種FFT單獨處理或只采用Cooley-Tukey算法的方法相比,，本設計巧妙地將Good-Thomas算法與Cooley-Tukey算法結(jié)合起來，在硬件資源和成本消耗上都有很大的節(jié)省,，速度上也能滿足要求,，而且這種結(jié)構(gòu)很容易進行功能擴展，只需要調(diào)整內(nèi)部FFT單元的種類和數(shù)目即可,。這種大規(guī)?；旌匣鵉FT的實現(xiàn)方法對其他場合的大規(guī)模FFT有一定的普適性。
參考文獻
[1] 3GPP TS 36.211 v8.7.0：Physical Channels and Modulation(Release 8)[S].2009,，6.
[2] Uwe Meyer-Baese.數(shù)字信號處理的FPGA實現(xiàn)[M].劉凌,，胡永生譯.北京：清華大學出版社，2003.
[3] SUZUKI Y,，SONE T,，KIDO K.A new FFT algorithm of radix 3, 6 and 12[J].IEEE Trans on Acoustics，Speech and Signal Processing,，1986,，4.
[4] MUNDARATH J.Mixed radix DFTs for LTE Uplink. Freescale Semiconductor，Inc,，2008,，6.
[5] CHANG Wei Hsin，TRUONG Q.On the Fixed-Point accuracy analysis of FFT algorithms[J].IEEE Trans on Signal Processing,，2008,，56(10).
[6] 吳松炎，管云峰,，余松煜，等.非基2點FFT處理器的設計及實現(xiàn)[J].電視技術,，2007.
[7] 李小文,，李貴勇，陳賢亮,，等.第三代移動通信系統(tǒng),、信令及實現(xiàn)[M].北京：人民郵電出版社，2003.