模糊控制具有不依賴對象的數(shù)學(xué)模型,、魯棒性強,、能夠很好地克服傳動系統(tǒng)中模型參數(shù)變化和非線性等不確定因素的優(yōu)點，因此,，模糊控制在實際控制系統(tǒng)中得到廣泛應(yīng)用,。模糊控制器" title="模糊控制器">模糊控制器普遍采用的是離線進行模糊推理產(chǎn)生的模糊控制表，然后把控制表存儲在單片機中進行在線查表控制,，但模糊推理計算量大,，這給模糊控制器的設(shè)計和調(diào)整帶來了許多困難。此外,，模糊控制存在的一個較大的缺點是穩(wěn)態(tài)精度不高,。為此，人們提出了許多改進的方法^[1],，其中最直接的方法是增加模糊量化論域,。但是，當量化論域中元素,、控制規(guī)則的條數(shù)很多時，模糊推理計算控制表的運算量大大增加,。本文在MATLAB環(huán)境下,，研究了模糊推理算法，研制了模糊推理程序,。只要給出模糊控制器的輸入和輸出量的隸屬函數(shù)" title="隸屬函數(shù)">隸屬函數(shù)矩陣,、控制規(guī)則矩陣、模糊量的特征向量" title="特征向量">特征向量矩陣,，運行該程序就可得到模糊控制表,。該軟件使用方便，為模糊控制的研究和應(yīng)用提供了方便的條件,。
1 模糊推理概述
　　在模糊控制中,，關(guān)鍵是要求得模糊關(guān)系矩陣，應(yīng)用最多的是離線進行模糊推理產(chǎn)生控制表,，模糊推理是模糊控制器的核心,。這里以兩入一出、采用CRI推理方法及重心法解模糊的模糊控制器為例,，簡要介紹模糊推理過程,。


　　這里需要指出的是，把笛卡兒乘積看作一個n×1與一個1×m的矩陣合成,。計算結(jié)果是n×m模糊陣,，而( A_i×B_i)^T1表示把這個n×m模糊陣按行“拉直”成nm元模糊行向量，再轉(zhuǎn)置成nm元模糊列向量；(A^*×B^*)^T2的含義是：把A^*×B^*這個n×m模糊陣按行“拉直”成nm元模糊行向量,。
2 基于MATLAB實現(xiàn)模糊推理程序設(shè)計
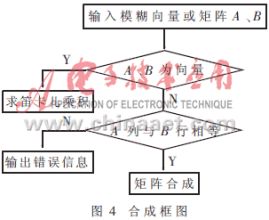
　　在MATLAB環(huán)境下,，充分利用其矩陣處理能力^[2]，可實現(xiàn)“∨—∧”,、“∨—· ”及 “∧—⊕”模糊算子運算,、重心法(或最大隸屬度法)解模糊。由于模糊推理過程涉及到合成,、求模糊關(guān)系及解模糊運算等,，采用自定義函數(shù)實現(xiàn)各個功能的模塊化。圖1為主函數(shù)程序框圖,；圖2為求模糊關(guān)系程序框圖,；圖3為解模糊程序框圖；圖4為合成程序框圖,。

　　運行此程序,，只要輸入矩陣A和B及相應(yīng)矩陣C、控制矩陣Q,、特征向量矩陣A^*和B^*及輸出量化論域矩陣QF,，就能得到模糊控制表。
3 計算實例
3.1 常規(guī)模糊控制器
　　下面以常規(guī)模糊控制器為例來驗證此程序的正確性,。在常規(guī)模糊控制器中,，輸入語言變量偏差E、偏差變化率CE,、輸出語言變量控制量U的賦值表及E,、CE→U的控制規(guī)則表見文獻^[3]。文獻^[3]中的原控制表如表1所示,，利用本文編制的模糊推理程序(采用“∨—∧”算子,、最大隸屬度解模糊)得到的控制表如表2所示。

　　在表1,、表2中最上面一行為輸入量誤差E的量化等級,，最左一列為輸入量誤差變化CE的量化等級。表1與表2中的數(shù)據(jù)存在差異,，這是因為表1中的帶*的數(shù)據(jù)均是修正后的結(jié)果,。這一點可以通過特征展開近似推理方法^[4]進行驗證。具體驗證方法如下：
　　以表1的第10行第7列為例,，即E^*＝(0,、0、0,、0,、0,、0、1,、0,、0、0,、0,、0、0,、0),、CE^*＝(0、0,、0,、0、0,、0,、0、0,、0,、1、0,、0,、0)為其特征向量、由特征展開近似推理方法^[4]的式:
　　
　　可計算出α₃＝0.3,、α₄＝1、β₅＝0.7,、β₆＝0.7,、β₇＝0.1、(α₃∧β₅)U4＝0.3U₄,、(α₃∧β₆)U₃＝0.3U₃,、(α₃∧β₇)U₃＝0.1U₃、(α₄∧β₅)U₃＝0.7U₃,、(α₄∧β₆)U₂＝0.7U₂,、(α₄∧β₇)U₂＝0.1U₂、由其余50條規(guī)則得到的α_i或β_j總有一個為0,，故這一對模糊輸入得到的模糊輸出為：
　　U＝0.3U₄∪0.7U₃∪0.3U₃∪0.1U₃∪0.7U₂∪0.1U₂
　　 ＝(0,、0.14、0.49,、0.7,、0.49、0.56、0.7,、0.3,、0.15、0,、0,、0、0,、0,、0)
　　經(jīng)過解模糊得到精確輸出為：
　　u＝((－4)＋(－1))/2＝－2.5
3.2 增加模糊量化論域的模糊控制器
　　以增加模糊量化論域的模糊控制器為例進行模糊推理，計算出控制表,。取誤差E,、誤差變化CE和控制量U的量化論域均為：
　　{－10，－9,，－8,，－7，－6,，－5,，－4，－3,，－2,，－1，0,，1,，2，3,，4,，5，6,，7,，8，9,，10}
　　取誤差E,、誤差變化CE和控制量U的模糊論域均為：
　　 {NVB，NB,，NM,，NS，NVS,，ZO,，PVS,，PS，PM,，PB,，PVB}
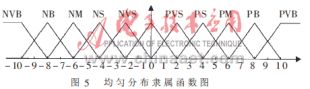
　　誤差E、誤差變化CE和控制量U的隸屬函數(shù)均如圖5所示,。

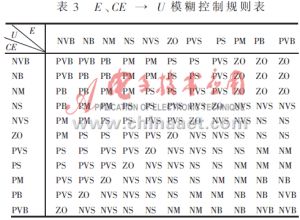
　　借鑒常規(guī)模糊控制器設(shè)計經(jīng)驗,，得到語言控制規(guī)則表、如表3所示,。表中共有121條控制規(guī)則,，其中一些規(guī)則可以合并。但利用計算機進行推理計算,，這些規(guī)則就沒必要合并了,。

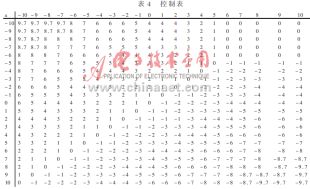
　　利用研制的模糊推理計算程序，采用“∨—,？”得到的E,，CE→U控制表，如表4所示,。在表中最上面一行為誤差E的量化等級,，最左一列為誤差變化CE的量化等級。
4 仿真結(jié)果
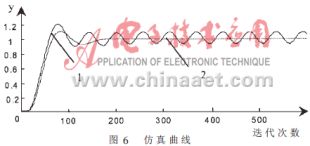
　　這里以對象
　　

　　為例,，分別使用表2,、表4中的數(shù)據(jù)構(gòu)成模糊控制器，響應(yīng)曲線如圖6中曲線1,、2所示,，其中采樣周期 T＝0.1s。從圖6中可以看出,，增加模糊量化論域的模糊控制器的穩(wěn)態(tài)精度明顯提高,。