FFT(快速傅里葉變換)是一種非常重要的算法,在信號(hào)處理、圖像處理、生物信息學(xué)、計(jì)算物理、應(yīng)用數(shù)學(xué)等方面都有著廣泛的應(yīng)用。在高速數(shù)字信號(hào)處理中,F(xiàn)FT的處理速度往往是整個(gè)系統(tǒng)設(shè)計(jì)性能的關(guān)鍵所在。FPGA(現(xiàn)場(chǎng)可編程門陣列)是一種具有大規(guī)模可編程門陣列的器件,不僅具有ASIC(專用集成電路)快速的特點(diǎn),更具有很好的系統(tǒng)實(shí)現(xiàn)的靈活性。基于FPGA的設(shè)計(jì)可以滿足實(shí)時(shí)數(shù)字信號(hào)處理的要求,在市
場(chǎng)競(jìng)爭(zhēng)中具有很大的優(yōu)勢(shì)。因此,F(xiàn)PGA為高速FFT算法的實(shí)現(xiàn)提供了一個(gè)很好的平臺(tái)。
1 FFT算法的硬件實(shí)現(xiàn)
1.1 系統(tǒng)框圖
本設(shè)計(jì)利用流水線技術(shù)來提高系統(tǒng)的性能,系統(tǒng)框圖,如圖1所示。其中,地址產(chǎn)生單元生成RAM讀寫地址,寫使能信號(hào)以及相關(guān)模塊的啟動(dòng)、控制信號(hào),是系統(tǒng)的控制核心;4點(diǎn)蝶形運(yùn)算單元的最后一級(jí)輸出不是順序的;旋轉(zhuǎn)因子產(chǎn)生單元生成復(fù)乘運(yùn)算中的旋轉(zhuǎn)因子的角度數(shù)據(jù);旋轉(zhuǎn)因子ROM中預(yù)置了每一級(jí)運(yùn)算中所需的旋轉(zhuǎn)因子。

在FPGA設(shè)計(jì)中,為提高系統(tǒng)的運(yùn)行速度,而將指令分為幾個(gè)子操作,每個(gè)子操作由不同的單元完成,這樣,每一級(jí)的電路結(jié)構(gòu)得到簡(jiǎn)化,從而減少輸入到輸出間的電路延時(shí),在較小的時(shí)鐘周期內(nèi)就能夠完成這一級(jí)的電路功能。在下一個(gè)時(shí)鐘周期到來時(shí),將前一級(jí)的結(jié)果鎖存為該級(jí)電路的輸入,這樣逐級(jí)鎖存,由最后一級(jí)完成最終結(jié)果的輸出。也就是說,流水線技術(shù)是將待處理的任務(wù)分解為相互有關(guān)而又相互
獨(dú)立、可以順序執(zhí)行的子任務(wù)來逐步實(shí)現(xiàn)。本設(shè)計(jì)中,4點(diǎn)蝶形運(yùn)算單元、旋轉(zhuǎn)因子復(fù)乘模塊以及最后的精度截取模塊采用流水線技術(shù)來處理。
1.2 基4蝶形運(yùn)算算法原理

式(1)為基4蝶形運(yùn)算單元的一般表達(dá)式,其中,![]() ,N為FFT運(yùn)算的點(diǎn)數(shù),本設(shè)計(jì)中為1 024,p為旋轉(zhuǎn)因子W的相位角,其規(guī)律將在1.4節(jié)討論。X(0)、X(1)、X(2)、X(3)為原始數(shù)據(jù),順序輸入RAM后蝶形倒序輸出,與旋轉(zhuǎn)因子復(fù)乘再進(jìn)行4點(diǎn)蝶形運(yùn)算,而X1(0)、X1(1)、X1(2)、X1(3)即為第1級(jí)蝶形運(yùn)算的結(jié)果。此時(shí)RAM存儲(chǔ)的原始數(shù)據(jù)已經(jīng)清空,將第1級(jí)蝶形運(yùn)算結(jié)果再存回RAM中,按照一定的地址輸出后,與第2級(jí)的旋轉(zhuǎn)因子復(fù)乘、4點(diǎn)蝶形運(yùn)算,得到第2級(jí)蝶形運(yùn)算結(jié)果,依此類推。由于蝶形運(yùn)算為同址操作,所以第2級(jí)的RAM寫地址即為第一級(jí)的RAM讀地址,每一級(jí)的RAM讀地址規(guī)律將在1.3節(jié)中討論。
,N為FFT運(yùn)算的點(diǎn)數(shù),本設(shè)計(jì)中為1 024,p為旋轉(zhuǎn)因子W的相位角,其規(guī)律將在1.4節(jié)討論。X(0)、X(1)、X(2)、X(3)為原始數(shù)據(jù),順序輸入RAM后蝶形倒序輸出,與旋轉(zhuǎn)因子復(fù)乘再進(jìn)行4點(diǎn)蝶形運(yùn)算,而X1(0)、X1(1)、X1(2)、X1(3)即為第1級(jí)蝶形運(yùn)算的結(jié)果。此時(shí)RAM存儲(chǔ)的原始數(shù)據(jù)已經(jīng)清空,將第1級(jí)蝶形運(yùn)算結(jié)果再存回RAM中,按照一定的地址輸出后,與第2級(jí)的旋轉(zhuǎn)因子復(fù)乘、4點(diǎn)蝶形運(yùn)算,得到第2級(jí)蝶形運(yùn)算結(jié)果,依此類推。由于蝶形運(yùn)算為同址操作,所以第2級(jí)的RAM寫地址即為第一級(jí)的RAM讀地址,每一級(jí)的RAM讀地址規(guī)律將在1.3節(jié)中討論。
1024點(diǎn)的基4-FFT共需要5級(jí)蝶形運(yùn)算,每級(jí)需要計(jì)算256個(gè)蝶形,其傳統(tǒng)實(shí)現(xiàn)框圖如圖2所示。
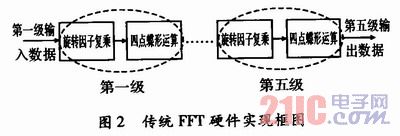
考慮到第一級(jí)蝶形運(yùn)算不需要旋轉(zhuǎn)因子,所以第一級(jí)的旋轉(zhuǎn)因子復(fù)乘模塊可以省略,但本設(shè)計(jì)的硬件結(jié)構(gòu)需要循環(huán)利用,一般情況下,可以對(duì)第一級(jí)數(shù)據(jù)進(jìn)行×1運(yùn)算,再進(jìn)行4點(diǎn)蝶形運(yùn)算。不過,考慮到我們并不關(guān)心每一級(jí)蝶形運(yùn)算后的結(jié)果,本文提出了一種蝶形運(yùn)算的新結(jié)構(gòu):即先進(jìn)行前一級(jí)的4點(diǎn)蝶形運(yùn)算,再進(jìn)行本級(jí)的與旋轉(zhuǎn)因子復(fù)乘運(yùn)算,如圖3所示。
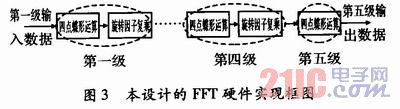
可以看出,圖3減少了一個(gè)旋轉(zhuǎn)因子復(fù)乘模塊,不但節(jié)約了一次乘法運(yùn)算時(shí)間,也省略了第一級(jí)旋轉(zhuǎn)因子,更好地利用了硬件結(jié)構(gòu)。
首先,在QuartusⅡ環(huán)境中對(duì)4點(diǎn)蝶形運(yùn)算時(shí)序仿真,采用流水線設(shè)計(jì),連續(xù)輸入連續(xù)輸出,仿真結(jié)果如圖4所示。

由圖4可以看出,輸出比輸入延時(shí)6個(gè)時(shí)鐘,這在系統(tǒng)的控制核心地址產(chǎn)生單元的設(shè)計(jì)中需要考慮到。
1.3 地址產(chǎn)生與時(shí)序控制
對(duì)于1 024.點(diǎn)基4 FFT運(yùn)算,需要5級(jí)蝶形運(yùn)算,每一級(jí)運(yùn)算都要有寫地址和讀地址,根據(jù)FFT同址運(yùn)算的特點(diǎn)可知,當(dāng)前的寫地址即是上一級(jí)蝶形運(yùn)算的讀地址。因此完成FFT運(yùn)算需要設(shè)計(jì)6級(jí)RAM地址。其中第1級(jí)的寫地址即是數(shù)據(jù)輸入的順序地址,不予討論。最后一級(jí)讀地址為數(shù)據(jù)正序輸出所需的地址。其余4級(jí)為1 024點(diǎn)數(shù)據(jù)對(duì)應(yīng)的FFT蝶形運(yùn)算。
第一級(jí)讀取節(jié)點(diǎn)地址的順序應(yīng)該是:(0,256,512.768),(1,257,513,769),……,(255,511.767,1 023)。易觀察其讀地址的規(guī)律如下:設(shè)讀取次序的二進(jìn)制編碼為bit[9:0];則讀地址的二進(jìn)制編碼為{bit[1:O],bit[9:2]},并且依次可以推出第2、3、4級(jí)的讀地址二進(jìn)制編碼分別為{bit[9:8],bit[1:0],bit[7:2]},{bit[9:6],bit[1:0],bit[5:2]}、{bit[9:4],bit[1:0],bit[3:2]},而最后一級(jí)輸出數(shù)據(jù)的地址二進(jìn)制編碼則為:{bit[1:0],bit[3:2],bit[5:4],bit[7:6],bit[9:8]}。圖5給出了第1級(jí)讀地址和第2級(jí)讀地址的部分?jǐn)?shù)據(jù),也可以看出第2級(jí)的寫地址即是第1級(jí)的讀地址。
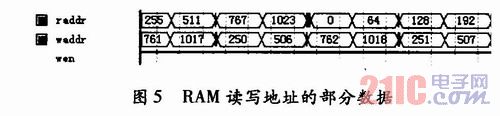
圖1中的地址產(chǎn)生單元作為系統(tǒng)的控制核心,不僅要生成每一級(jí)的RAM讀寫地址,還要產(chǎn)生RAM寫使能信號(hào)、輸出有效信號(hào)以及4點(diǎn)蝶形運(yùn)算單元和旋轉(zhuǎn)因子產(chǎn)生單元的啟動(dòng)信號(hào),由于時(shí)序電路還需要考慮器件延時(shí),例如上文提到的4點(diǎn)蝶形運(yùn)算輸出比輸入延時(shí)6個(gè)時(shí)鐘,以及RAM存取數(shù)據(jù)輸出比輸入延時(shí)1個(gè)時(shí)鐘,這些都需要在控制核心中考慮到。
1.4 旋轉(zhuǎn)因子產(chǎn)生
對(duì)于1 024點(diǎn)FFT蝶形運(yùn)算,需要1 024個(gè)旋轉(zhuǎn)角度(即2π的1 024等份),其中第一級(jí)不需要復(fù)乘運(yùn)算,第6級(jí)只是將數(shù)據(jù)進(jìn)行整序沒有運(yùn)算單元,其他4級(jí)都需要旋轉(zhuǎn)因子。本設(shè)計(jì)采用將旋轉(zhuǎn)因子預(yù)置于ROM中,通過查找表方法得出每一級(jí)運(yùn)算的所需的旋轉(zhuǎn)因子。根據(jù)旋轉(zhuǎn)因子的可約性,后幾級(jí)運(yùn)算所需的旋轉(zhuǎn)因子都可以在第一級(jí)運(yùn)算的旋轉(zhuǎn)因子中找到,因此無需另外存儲(chǔ)。旋轉(zhuǎn)因子在ROM中的存儲(chǔ)規(guī)律是:旋轉(zhuǎn)因子相位角p處存儲(chǔ)旋轉(zhuǎn)因子W=*****。定義一個(gè)10 bit的計(jì)數(shù)器count[9:0],則第2、3、4、5級(jí)ROM的相位角規(guī)律按照Verilog語法可表示為

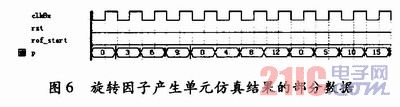
為了節(jié)省資源,本設(shè)計(jì)只在ROM單元中存儲(chǔ)了前256個(gè)旋轉(zhuǎn)因子數(shù)據(jù),即第一象限因子![]() 其余象限的因子可通過象限轉(zhuǎn)換后得到,這樣就大大節(jié)省了存儲(chǔ)單元的硬件資源。圖6為旋轉(zhuǎn)因子產(chǎn)生單元在QuartusⅡ環(huán)境中仿真結(jié)果的部分?jǐn)?shù)據(jù)。
其余象限的因子可通過象限轉(zhuǎn)換后得到,這樣就大大節(jié)省了存儲(chǔ)單元的硬件資源。圖6為旋轉(zhuǎn)因子產(chǎn)生單元在QuartusⅡ環(huán)境中仿真結(jié)果的部分?jǐn)?shù)據(jù)。
2 系統(tǒng)仿真結(jié)果
輸入數(shù)據(jù)為s=1 024×cos(2π×f_in×t),其中f_in=50 M,F(xiàn)s=80 MHz,n=40,t=0:1/Fs:(n-1)/Fs,利用QuartusⅡ軟件對(duì)系統(tǒng)在100 MHz的時(shí)鐘環(huán)境下進(jìn)行了仿真,將仿真輸出結(jié)果轉(zhuǎn)換成tbl文件并利用Matlab軟件讀取后,得到如圖7所示的頻譜數(shù)據(jù)圖(實(shí)部數(shù)據(jù)部分)。
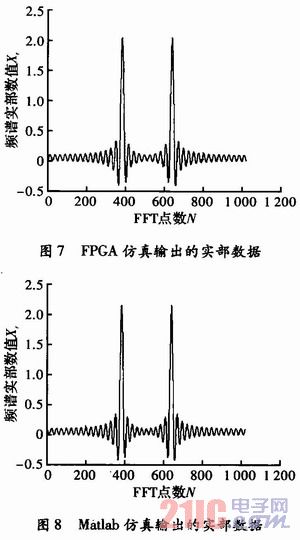
圖8所示為Maflab自帶FFT函數(shù)對(duì)于輸入相同1 024點(diǎn)數(shù)據(jù)的FFT計(jì)算結(jié)果(同樣為實(shí)部數(shù)據(jù)部分)。
通過比較可以看到,本設(shè)計(jì)的仿真結(jié)果與Matlab的仿真結(jié)果基本一致,可以正確高效地計(jì)算出1 024點(diǎn)FFT數(shù)據(jù)。
3 結(jié)束語
本設(shè)計(jì)全部由Verilog HDL語言實(shí)現(xiàn),采用自頂向下的設(shè)計(jì)方法,完成了一種基于FPGA的1 024點(diǎn)16位FFT算法,共需要5級(jí)運(yùn)算,每級(jí)需要計(jì)算256個(gè)蝶形。提出了將蝶形運(yùn)算先進(jìn)行前一級(jí)的蝶形加減運(yùn)算,再進(jìn)行本級(jí)的與旋轉(zhuǎn)因子復(fù)乘運(yùn)算的結(jié)構(gòu)。由前所述,平均每個(gè)蝶形運(yùn)算需要4個(gè)時(shí)鐘周期,所以理論上完成1 024點(diǎn)FFT的總時(shí)鐘周期為N=256×4×5=5 120;假設(shè)使用的時(shí)鐘為100MHz,那么將耗時(shí)T=5 120×(1/100)=51.2μs,這與仿真結(jié)果51.32μs基本一致。

