引 言

　　電力系統(tǒng)運(yùn)行的穩(wěn)定性是電力系統(tǒng)安全運(yùn)行的基本要求，而對同步發(fā)電機(jī)勵磁的控制是改善電力系統(tǒng)運(yùn)行穩(wěn)定性的一個經(jīng)濟(jì)和有效的手段,。通過對發(fā)電機(jī)勵磁施加適當(dāng)?shù)目刂?，可以改善電力系統(tǒng)在大小擾動下的穩(wěn)定性[1-3]。以往勵磁控制器設(shè)計通常是基于運(yùn)行點(diǎn)的線性化方法所得,，將電力系統(tǒng)近似作為一個線性化系統(tǒng)進(jìn)行處理。但是電力系統(tǒng)的非線性決定了這種方法的局限性,?；谖⒎謳缀卫碚摰臓顟B(tài)反饋精確線性化方法被引入發(fā)電機(jī)勵磁控制系統(tǒng)設(shè)計[6]，但是這種方法需要復(fù)雜的微分幾何數(shù)學(xué)工具,，作為改進(jìn),，文獻(xiàn)[7-9]提出基于直接反饋線性化理論的非線性勵磁控制器。本文提出一種基于輸入對狀態(tài)反饋線性化的非線性勵磁控制器,，這種方法實(shí)用方便,，容易理解。本文對這種新型的勵磁控制器進(jìn)行詳細(xì)的仿真研究,，仿真結(jié)果證明這種非線性勵磁控制器對于提高電力系統(tǒng)在大小擾動下的穩(wěn)定性有一定作用,。

2 輸入對狀態(tài)反饋線性化理論簡述
　　對于給定單輸入仿射非線性系統(tǒng)：
　　
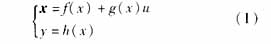
　　系統(tǒng)(1)能夠被輸入對狀態(tài)反饋線性化的條件是:系統(tǒng)具有相對度(relative degree)r=n，其中n為系統(tǒng)的階數(shù),。若非線性系統(tǒng)(1)能夠被輸入對狀態(tài)反饋線性化,。則在一個鄰域Ω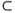Rn中存在一個微分同胚T:Ω→Rn，在新的坐標(biāo)變換下z=T(x)下,，系統(tǒng)可以轉(zhuǎn)化為:
　
　
　　同時可得到a(x),，B(x)的表達(dá)式，如下(4)式所示,。
　
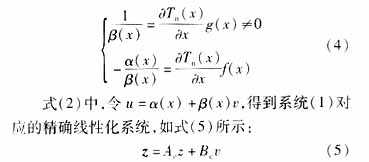
　　式(5)是一線性化系統(tǒng),，所以其控制規(guī)律可以完全按照線性系統(tǒng)的方法來設(shè)計。

3 非線性勵磁控制設(shè)計
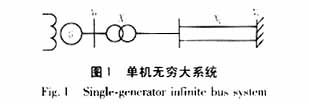
　　 所要研究的系統(tǒng)如圖1所示,，發(fā)電機(jī)采用三階簡化模型,，保持原動機(jī)功率不變，并且忽略摩擦阻尼的影響情況下,，系統(tǒng)可用下面一組微分方程表示:
　
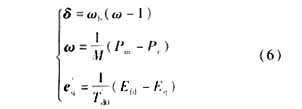
其中：δ為發(fā)電機(jī)功角,，Wb=2πf，W為發(fā)電機(jī)角頻率,，Pm為原動機(jī)功率,，Pe為發(fā)電機(jī)電磁功率，e′q為暫態(tài)電勢,，Efd為勵磁電壓,，Eq為空載電勢,。M為慣性時間常數(shù)，T′do為勵磁繞組暫態(tài)時間常數(shù),。

 
系統(tǒng)方程可以寫成：
　
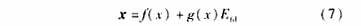
　　由于該系統(tǒng)可以實(shí)現(xiàn)輸入對狀態(tài)反饋線性化,，所以存在可逆變換z=T(x)=(T1(x) T2(x) T3(x))T將系統(tǒng)轉(zhuǎn)換為(5)形式。由(3)可得：
　
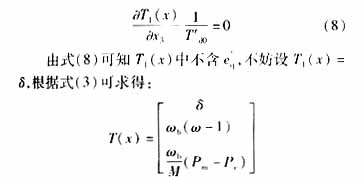
    其逆變換T-1(z)存在,。根據(jù)(4)式,，可求得a(x)、β(x)
　
　
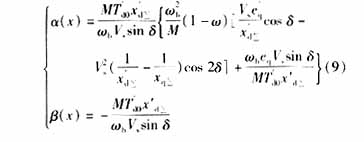
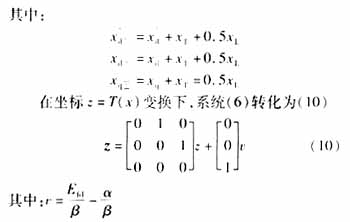
　　系統(tǒng)(10)為一線性系統(tǒng),，可以按照線性最優(yōu)控制[10]設(shè)計控制量,，控制量表達(dá)式如下式(11)所示：
　
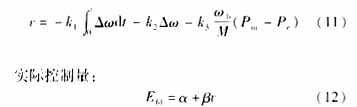
    可以證明，用輸入對狀態(tài)反饋線性化方法推導(dǎo)出的控制規(guī)律和用基于微分幾何理論的狀態(tài)反饋精確線性化方法以及用直接反饋線性化(DFL)方法推導(dǎo)出的控制規(guī)律一致[6][8][9],，但本文的方法更簡單實(shí)用,。
　
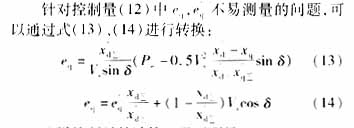
    這樣控制量的計算只需要測量δ, W,Pe。

4 仿真結(jié)果
    針對圖1所示系統(tǒng),，分別對系統(tǒng)發(fā)生(1)三相短路0.2s后切除故障,；以及(2)切除一條線路運(yùn)行3.5m后恢復(fù)雙回線路運(yùn)行兩種擾動下的動態(tài)過程進(jìn)行了仿真。仿真結(jié)果如圖2,，圖3所示,。

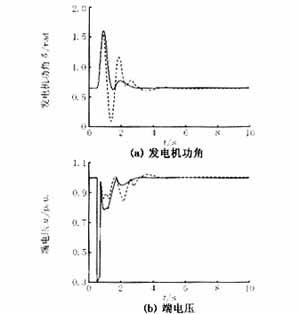
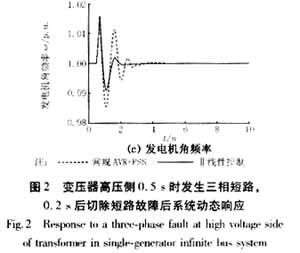
    從圖2,圖3可以看出，本文提出的非線性勵磁控制器在系統(tǒng)發(fā)生擾動時,，總是表現(xiàn)出比常規(guī)的AVR+PSS更好的阻尼特性,，因此采用非線性勵磁控制器更能抑制系統(tǒng)在發(fā)生故障時的振蕩，對于增強(qiáng)系統(tǒng)穩(wěn)定性有一定促進(jìn)作用,。
    另外,，本文對圖4所示五臺機(jī)電力系統(tǒng)進(jìn)行了仿真研究，假定在No.3發(fā)電機(jī)出口端發(fā)生三相短路時,，在No.3機(jī)上裝常規(guī)的AVR+PSS或者非線性勵磁控制器,，考察多機(jī)系統(tǒng)的動態(tài)響應(yīng)情況，仿真結(jié)果如圖5所示,。

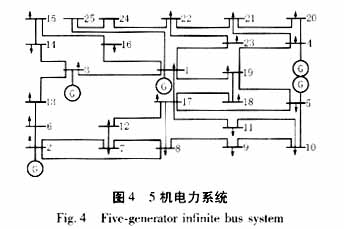
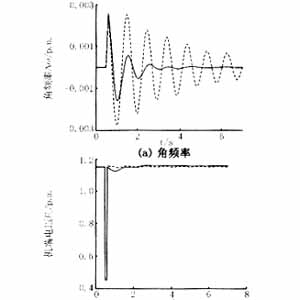
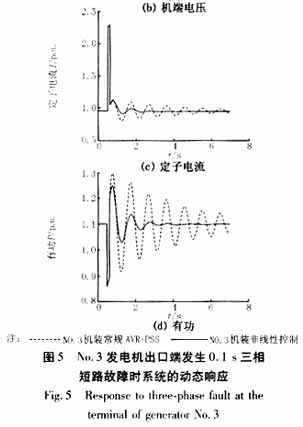
    由圖5可以看出,，當(dāng)發(fā)電機(jī)裝上本文提出的非線性勵磁控制器后，在系統(tǒng)發(fā)生故障時,，比起常規(guī)的AVR+PSS,能夠更快的平息振蕩,。

5 結(jié)論
    本文提出一種基于輸入對狀態(tài)反饋線性化理論的非線性勵磁控制器，所得的控制規(guī)律和用基于微分幾何理論的精確線性化思想推導(dǎo)出的控制規(guī)律具有一致性,，但是本文的方法更簡單實(shí)用,，利于工程應(yīng)用。單機(jī)無窮大系統(tǒng)以及多機(jī)系統(tǒng)下的仿真結(jié)果證明,，該非線性勵磁控制器和常規(guī)AVR+PSS相比,，能夠更好抑制電力系統(tǒng)在大小擾動下振蕩,，對于增強(qiáng)系統(tǒng)穩(wěn)定性有一定作用。