1 引 言

A.Fabre等提出的電流控制傳送器(CCCII),，克服了電流傳送器(CCII)的X端存在的寄生電阻導(dǎo)致的基于CCII電路產(chǎn)生的傳輸函數(shù)的誤差。同時,，與OTA相比,，對于同一偏置電流,，CCCII的電導(dǎo)Gx比OTA的跨導(dǎo)Gm大4倍，因而提高了頻響,，降低了功耗,，且電路結(jié)構(gòu)簡單，受到了國內(nèi)外學(xué)者的高度重視,?；贑CCII的二階濾波器及高階濾波器不斷提出，但對高階多功能電流模式濾波器的研究還明顯不足,。

本文基于梅森信號流圖理論,，討論了n階濾波器的信號流圖設(shè)計方法，成功設(shè)計出了一種新穎的基于CCCII和MOCCCII實現(xiàn)的n階多功能濾波器電路模型,，該電路能實現(xiàn)低通,、高通和帶通濾波功能。該電路結(jié)構(gòu)簡單,，含有最少的元件,，且電路中所有電容均接地，易于集成,。

2 電路理論與設(shè)計方法

2.1 CCCII簡介

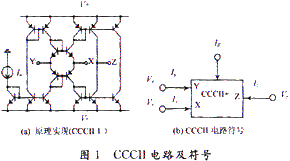
Fabre等提出的CCCII+實現(xiàn)原理及電路如圖1(a)所示,，電路符號如圖1(b)所示，其端口傳輸特性為：

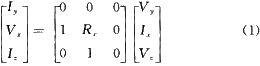
Rx為經(jīng)X端的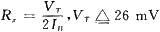寄生電阻,，,。可見,，Rx受偏置電流IB的控制,。


 

多端輸出MOCCCII是在CCCII的基礎(chǔ)上用電流復(fù)制的方法得以實現(xiàn)，他能等比例地輸出多個電流,，其理想端口特性為：
 

2.2 電路實現(xiàn)

設(shè)基于電流模式n階低通,、高通、帶通濾波器的傳遞函數(shù)的一般表達(dá)式為：

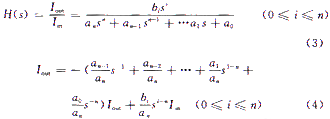
根據(jù)梅森信號流圖思想,，式(4)可由n條反饋通路和1條前向通路構(gòu)成,，并得信號流圖如圖2所示。

 

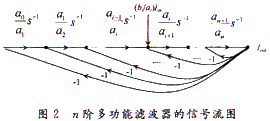
根據(jù)信號流圖,，可利用CCCII實現(xiàn)積分器和比例放大器,，用MOCCCII多端輸出實現(xiàn)反饋，形成電路,，如圖3所示,。

 

為了實現(xiàn)MOCCCII的反饋作用，必須設(shè)計R2,，使得R2等于MOCCCII的寄生電阻Rx0,，即：

R2=Rx0

第n+1個CCCII的作用是實現(xiàn)比例放大,，通過調(diào)節(jié)R1和其寄生電阻Rx的比值，可實現(xiàn)對增益的調(diào)節(jié),。當(dāng)bi=ai時,，圖3中的Iin可直接連接至CCCII的輸入端。

對比式(3)與圖3,，不難看出有下列參數(shù)關(guān)系：

其中：Rxj為第j個CCCII X端的寄生電阻,。

從式(3)可以看出，適當(dāng)選擇電流輸入端,，能實現(xiàn)不同功能的濾波器。

(1) 低通：取i=0,，即電流從第一個CCCII輸入端輸入,。

(2) 高通：取i=n，即電流從MOCCCII的輸入端輸入,。

(3) 帶通：當(dāng)n為偶數(shù)時,，取i=n／2；當(dāng)n為奇數(shù)時,，取i=(n±1)／2,，即電流從第i+1個CCCII輸入端輸入。

3 設(shè)計實例與計算機仿真

為說明本文所提方法的可行性,，對最平坦型Butter-worth截止頻率為500 kHz的4階低通,、高通、帶通濾波器進行設(shè)計,。經(jīng)分析取R1=R2=Rx1=Rx2=Rx3=Rx4=Rx0=1 kΩ,，C1=832.169 7 pF，G2=416.1011 pF,，C3=243.751 7 pF,，G4=121.879 6 pF，其仿真結(jié)果如圖4所示,。

作者還對該電路的2,，4，6階截止頻率為500 kHz的巴特沃茲低通濾波器進行了PSpice仿真,，結(jié)果如圖5所示,，由此可以看出，隨著階數(shù)的增高,，過渡帶減小,，幅頻特性越好。

 

4 結(jié) 語

本文基于梅森信號流圖理論,，討論了n階多功能CCCII濾波器的信號流圖設(shè)計方法,，成功地設(shè)計出了一種新穎的基于CCCII實現(xiàn)的n階多功能濾波器電路模型,，該電路有如下優(yōu)點：

(1) 設(shè)計方法簡單；

(2) 通過選擇不同的輸入點,，便可實現(xiàn)低通,、帶通、高通的濾波功能,；

(3) 含有最少的元件(n或n+1個CCCII,，一個MOC-CCII，n個電容,，1個或2個電阻),；

(4) 通過對CCCII偏置電流的控制，可實現(xiàn)濾波器的極點角頻率的電調(diào)諧,；

(5) 所有的電容均接地,，易于集成。