摘  要： 不直接考慮氣候等隨機因素,，根據過去貴州電網短期負荷時間序列，利用小數據量方法計算最大李雅普諾夫指數,，并通過李雅普諾夫指數定義的性質對貴州電網短期負荷時間序列進行混沌性仿真檢驗,，結果具有混沌性。
關鍵詞： 電網短期負荷,；時間序列,；小數據量；李雅普諾夫指數,；混沌性

    近年來,，混沌理論這門新興學科在科學研究中的地位日漸凸顯,。混沌作為一個新的研究方向,，已滲透到自然科學和社會科學的各個領域,。對于混沌，目前尚無通用的嚴格定義,，一般把不是由隨機性外因引起的,，而是由確定性方程(內因)直接得到的具有隨機性的運動狀態(tài)稱為混沌。也就是說：混沌是確定性系統表現出來的貌似隨機的運動,，是對初始條件十分敏感的長期有界的動態(tài)行為,。混沌不是無序,，而是包含著嚴格的內在規(guī)律?；煦缪芯勘砻鳎杭词故亲詈唵蔚姆蔷€性系統仍然可以表現出非常復雜的動力學行為,。在電力系統領域，已有大量混沌性質方面的研究,。例如：電力經濟中的混沌,，機電系統混沌振蕩，分叉,、混沌與電壓驟降,，水輪發(fā)電機組調速系統中控制器參數誘發(fā)的混沌，靜態(tài)負荷模型辨識,，電站經濟運行最優(yōu)負荷分配,，模糊電力系統穩(wěn)定器的參數優(yōu)化，短期負荷預測,，以及電氣設備狀態(tài)監(jiān)測中信號的檢測方面等,。通過研究混沌，人們對事物有了更加深入的了解,。目前,，電力系統對混沌現象分析主要采用的方法有：龐加萊映射、Lyapunov(李雅普諾夫)指數計算,、Melnikov(梅爾尼科夫)方法和頻譜分析等,。本文運用李雅普諾夫指數法對貴州電網短期負荷時間序列展開研究[1]。
1 李雅普諾夫指數
    混沌運動的基本特點是運動對初值條件極為敏感,。兩個很靠近的初值所產生的軌道,，隨時間推移按指數方式分離，Lyapunov指數就是定量描述這一現象的量,。
1.1 概念及性質
    本文研究的貴州電網短期負荷時間序列屬于一維動力系統,。
    對于一維映射：
  
  
    一維映射只有一個李雅普諾夫指數,，它可能大于、等于或小于零,。由上面的討論得知,，若λ<0，則意味著相鄰點最終要靠攏合并成一點,，這對應于穩(wěn)定的不動點和周期運動,；若λ=0，則各點對應周期倍分岔點,；若λ>0,，則意味著相鄰點最終要分離，根據敏感的初始條件,，其對應于混沌運動,。可見,，λ由負變?yōu)檎砻髁诉\動向混沌的轉變,，故λ>0可作為系統混沌行為的一個判據[2]。
1.2 小數據量方法
    計算李雅普諾夫指數的方法有：定義法,、wolf方法,、Jacobian方法、p-范數方法,、小數據量方法等,。綜合各種方法的難易度以及計算李雅普諾夫指數的準確度，決定采用小數據量方法計算最大李雅普諾夫指數[3],。該方法的優(yōu)點在于：(1)對小數據組可靠,；(2)計算量并不大；(3)相對容易操作,；(4)計算精度較其他方法有明顯的改善,。小數據量方法的整個計算過程如圖2所示。

2 最大李雅普諾夫指數計算
    目前,，人們計算最大Lyapunov指數常用wolf的軌線算法,，但是軌線法具有明顯的缺陷。首先,，用此法計算所得結果經常不準確,。原因在于按軌線算法尋找不到滿足條件的新的鄰域軌道時，研究者必須使用較差的軌道,，不難想到,，較差的軌道使得后來計算出現誤差。其次,，軌線算法受嵌入參數的影響明顯,，這是因為嵌入參數影響了重構相空間的形狀,。但此方法不可避免地要對嵌入參數作出猜測。除此,，有人也用矩陣算法來計算最大Lyapunov指數,，而矩陣算法的一個明顯缺陷是計算過程過于繁難，不易實施,。因此,，本文采用另一種新方法——小數據量法來計算最大Lyapunov指數值。在混沌研究和實際應用中,，有時并不需要計算出時間序列的所有Lyapunov指數譜,，而只要計算出最大Lyapunov指數就足夠了。故判斷一個時間序列是否為混沌系統,，只要看最大Lyapunov指數是否大于零就能得出結論,。
2.1 用快速傅里葉變換(FFT)估計時間延遲τ和平均周期P
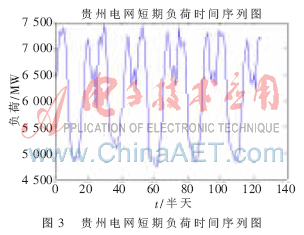
    本文收集貴州電網短期負荷時間序列為：貴州電網2009年7月1日到8月31日的負荷值。每隔一個小時取一個負荷值,，共1 488個值,。
    對貴州電網負荷時間序列進行描點，畫出貴州電網短期負荷時間序列圖,，如圖3所示。從圖中可以看出,，貴州電網短期負荷時間序列波形變化具有一定的相似性,。

    不直接考慮氣候等隨機因素，利用貴州電網短期負荷時間序列進行FFT變換,，根據自相關函數法：對負荷時間序列,，先寫出其自相關函數，然后作出自相關函數關于時間τ的函數圖像,，如圖4所示,。由數值試驗結果，當自相關函數(縱坐標)下降到初始值的1－1/e(大約為0.63)時,，所得的時間τ(橫坐標)就是重構相空間的時間延遲τ(τ取正整數),。

    由圖4中看出，當自相關函數下降至大約0.63時,，所對應的時間大約為3.6,，所以得出短期負荷時間序列的時延為4 h。平均周期通過能量光譜的平均頻率的倒數估計出來,，由MATLAB編程計算得出P為24,。
2.2 計算嵌入維數m
    由Grassberger和Procaccia提出的G-P算法計算關聯維數d。通過關聯維數d與嵌入維數m的關系：m≥2d+1確定m的值[4],。
    此算法依據的方法是：寫出時間序列的關聯函數C(r),，r為一個給定的值,。對于r的某個適當范圍，滿足d(m)=ln C(r)/ln r,。通過增加嵌入維數m,，重復計算C與d，直到相應的維數估計值d不再隨m的增長而增長,，在一定誤差范圍內不變?yōu)橹?。從而由擬合求出對應于m的關聯維數估計值d。由MATLAB編程調試繪出不同m下d的ln C-ln r曲線(為方便編程,，ln C等同于ln C(r)),，如圖5所示，其直線部分的斜率就是關聯維數d,。得出d=1.808 9,，2.185 7，2.404 7,，2.303 9,，2.301 4，2.331 9,，2.341 0,，2.348 5，2.355 5,，2.356 6,，2.359 9，2.374 3,，2.386 1,，2.398 8，2.406 3,，2.416 2,，2.418 9，2.434 0,，2.443 7,。
    對應d隨m變化的曲線圖如圖6所示。m從2開始,，根據圖6得出：當m為10,、11、12時,，關聯維數d趨于平穩(wěn),，故m取11。

2.3 重構相空間
    相空間重構是從時間序列出發(fā)創(chuàng)建一個多維狀態(tài)空間,，它保持了原系統的許多幾何不變量不變,，這些幾何不變量包括不動點的特征值,、吸引子的分維數和軌線的Lyapunov指數等[5]。
    根據時間延遲τ和平均周期P重構相空間Yj,，并且找最近點,，限制短暫分離。對相空間中每個點Yj,，計算出該鄰點對經過i個離散時間步長后的距離dj(i),；之后對每個i，求出所有j的ln dj(i)平均值y(i),，測量平均分離,，即：

    最后用最小二乘法作出擬合直線，該直線的斜率就是最大Lyapunov指數λ1,，如圖7所示,。

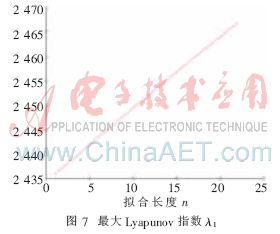
    根據MATLAB編程調試，作擬合直線計算得出λ1為0.003 1,。
    由最大Lyapunov指數λ1>0,，得出貴州電網短期負荷時間序列具有混沌性。這也為今后利用混沌理論更加深入地對貴州電力系統作出進一步的研究打下了基礎,。針對電網短期負荷的研究,，現在應用最多的就是短期負荷預測。短期負荷預測是電力系統的一項基本工作,，是安排開停機機組計劃的基礎,，其預測精度直接影響電力系統的經濟效益[6]?；煦缋碚撛诙唐陔娏ω摵深A測中的應用也逐漸增多?；煦缋碚搶ω摵尚蛄心苓M行相空間重構,、分形維數計算、最大李雅譜諾夫理論指數計算以及不確定性檢驗,，對影響負荷變化因素的復雜性和隨機性有更強的適應性,，這可以彌補其他方法在收斂性和魯棒性等方面的局限性。
參考文獻
[1] 黃潤生,，黃浩.混沌及其應用(第二版)[M].武漢:武漢大學出版社,，2005:118-178.
[2] 呂金虎，陸君安,，陳士華.混沌時間序列分析及其應用[M].武漢:武漢大學出版社,，2002:72-109.
[3] ROSENSTEIN M T， COLLINS J J,， DE LUCA C J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D,， 1993(65):117-134.
[4] GRASSBERGER P,， PROCACCIA I. Measuring the strangeness of strange attractors[J]. Physica D， 1983(9):189-208.
[5] 王海燕,，盧山.非線性時間序列分析及其應用[M].北京:科學出版社,，2006:12-43.
[6] 劉晨輝.電力系統負荷預測理論與方法[M].哈爾濱:哈爾濱工業(yè)大學出版社，1987:77-112.