摘  要： 當(dāng)GPS信號(hào)發(fā)生阻塞時(shí),，可見(jiàn)衛(wèi)星數(shù)會(huì)不足4顆,，這時(shí)迭代最小二乘算法（ILS）與普通擴(kuò)展卡爾曼濾波(EKF)都不再適用。針對(duì)這一問(wèn)題提出了一種改進(jìn)的EKF算法,。該算法利用在垂直地面方向上的位置變化緩慢這一運(yùn)動(dòng)特性,，建立了改進(jìn)EKF算法的系統(tǒng)模型。通過(guò)理論分析得到了濾波器參數(shù),，最后利用真實(shí)的GPS衛(wèi)星數(shù)據(jù)進(jìn)行驗(yàn)證,。實(shí)驗(yàn)結(jié)果表明，在可見(jiàn)衛(wèi)星數(shù)不少于4顆時(shí),，此改進(jìn)的EKF算法定位精度與普通的EKF算法基本相同,；在GPS信號(hào)阻塞只有3顆可見(jiàn)衛(wèi)星時(shí)，此改進(jìn)的EKF算法的定位精度明顯優(yōu)于普通的EKF算法,。
關(guān)鍵詞： 擴(kuò)展卡爾曼濾波; GPS; 信號(hào)阻塞; 定位解算

    GPS衛(wèi)星定位解算是根據(jù)偽距,、偽距增量等測(cè)量值，計(jì)算接收機(jī)的位置P,、速度V和時(shí)間T等信息的過(guò)程,。目前GPS實(shí)時(shí)定位解算中最為常用的兩種方法為迭代最小二乘算法（ILS）和擴(kuò)展卡爾曼濾波（EKF）,。為了準(zhǔn)確計(jì)算接收機(jī)的三維位置以及時(shí)間未知數(shù)的值，解算過(guò)程需要至少4顆衛(wèi)星的測(cè)量信息,。但是當(dāng)GPS信號(hào)出現(xiàn)遮擋時(shí),，接收機(jī)只能接收到3顆衛(wèi)星的測(cè)量信息，解算方程就不夠4個(gè),，ILS不再適用,。參考文獻(xiàn)[1]引入EKF，利用隨著時(shí)間推移的多組數(shù)據(jù)進(jìn)行實(shí)時(shí)定位解算,，但定位精度也很難滿足用戶的需求,。
　為了解決上述問(wèn)題，本文提出了一種改進(jìn)的EKF算法,。利用在垂直地面方向上的位置變化緩慢這一運(yùn)動(dòng)特性,，建立了改進(jìn)EKF算法的系統(tǒng)模型，并通過(guò)理論分析得到了濾波器參數(shù),，最后利用真實(shí)的衛(wèi)星數(shù)據(jù)進(jìn)行驗(yàn)證,。需要特別指出的是，由于本文提出的改進(jìn)EKF算法利用的是在垂直地面方向上的位置變化緩慢的特征,，故而該算法的適用場(chǎng)合為車(chē)載等地面用戶的定位解算,，不適合在垂直地面方向上高速運(yùn)動(dòng)的情形。
1 定位解算的系統(tǒng)模型
　衛(wèi)星定位解算的系統(tǒng)模型包括狀態(tài)模型和觀測(cè)模型兩部分,。令向量yt,、xt分別表示系統(tǒng)模型的測(cè)量值和系統(tǒng)狀態(tài)參量：

1.1 測(cè)量模型
    系統(tǒng)的測(cè)量模型描述了系統(tǒng)測(cè)量值與系統(tǒng)狀態(tài)參量之間的關(guān)系。偽距與系統(tǒng)狀態(tài)參量的關(guān)系可表示為：

1.2狀態(tài)模型
    系統(tǒng)的狀態(tài)模型描述了系統(tǒng)狀態(tài)參量的時(shí)間更新過(guò)程,。由參考文獻(xiàn)[3-4]可知,，更新過(guò)程的表達(dá)式為：

式(9)中的T為采樣時(shí)間間隔。
式(8)中的wt表示系統(tǒng)狀態(tài)轉(zhuǎn)移的噪聲模型：

2 改進(jìn)的EKF
    根據(jù)第1節(jié)中建立的系統(tǒng)模型,，系統(tǒng)測(cè)量值yt為2參數(shù),，系統(tǒng)狀態(tài)參量xt為8參數(shù)，為了得到準(zhǔn)確解,，故而需要至少4顆有效衛(wèi)星的測(cè)量值,。為了能夠滿足用戶需求的定位精度，本文提出利用一般車(chē)輛行人等用戶在垂直地面方向上的位置變化緩慢這一運(yùn)動(dòng)特性,，增加如下方程：

式(17)中，R1為從用戶在ECEF坐標(biāo)系下的狀態(tài)參量xt到用戶在NED坐標(biāo)系下的狀態(tài)參量mt的轉(zhuǎn)換矩陣,，利用坐標(biāo)系旋轉(zhuǎn)的原理可以求得[2],。A2為用戶在NED坐標(biāo)系下的狀態(tài)參量mt的一步轉(zhuǎn)移矩陣。它們的表達(dá)式如下：

    綜上所述,，并結(jié)合參考文獻(xiàn)[5],，得到改進(jìn)的EKF算法的計(jì)算過(guò)程如下：
  
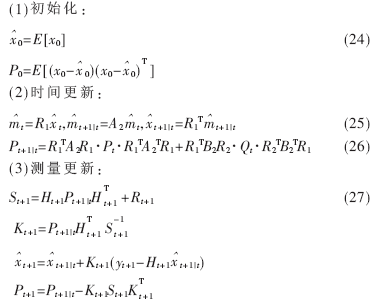
   根據(jù)理論分析可以得出,，改進(jìn)的EKF相對(duì)于普通的EKF來(lái)說(shuō)，增加了一項(xiàng)先驗(yàn)信息,，故而使得只有3顆有效衛(wèi)星時(shí)的定位解算有了4個(gè)解算方程,，因此可以相對(duì)準(zhǔn)確地解算出4個(gè)未知數(shù)的值；而在有效衛(wèi)星數(shù)不少于4顆時(shí),，增加的方程(15)仍然滿足,，故而也不會(huì)影響定位精度。
3 算法仿真和分析
　在本文的算法驗(yàn)證實(shí)驗(yàn)中,，使用了Leika GPS1200測(cè)量型接收機(jī)在車(chē)載動(dòng)態(tài)下采集的GPS信號(hào)的偽距和偽距增量的測(cè)量值,，其中偽距測(cè)量值經(jīng)過(guò)偽距增量測(cè)量值的平滑。算法的驗(yàn)證是在PC機(jī)上使用Matlab完成的,。
　在算法驗(yàn)證中,，設(shè)置采樣時(shí)間間隔為T(mén)=1 s。接收機(jī)的運(yùn)動(dòng)狀態(tài)為從靜止?fàn)顟B(tài)變化到在地面上高速運(yùn)動(dòng)最后又逐步靜止,。測(cè)試數(shù)據(jù)長(zhǎng)度為2 500 s,。參考軌跡是接收機(jī)使用動(dòng)態(tài)實(shí)時(shí)差分(RTK)方法測(cè)定的，方差精確至毫米級(jí),。分別在有效衛(wèi)星不少于4顆和只有3顆的情況下,，比較了幾種定位解算算法的定位結(jié)果。
3.1 有效衛(wèi)星數(shù)不少于4顆時(shí)的定位結(jié)果
　以有效衛(wèi)星數(shù)為4顆為例,，分別使用ILS,、EKF和改進(jìn)的EKF算法進(jìn)行定位，得到以ECEF坐標(biāo)系下XYZ三維坐標(biāo)表示的定位結(jié)果,，如圖1所示,。

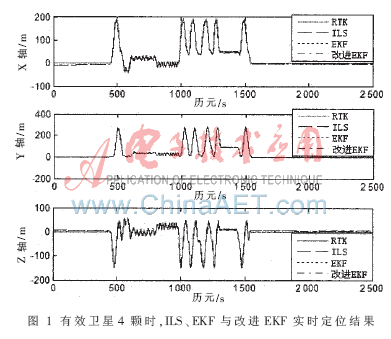
   由圖 1可知，接收機(jī)在前400 s時(shí)基本保持靜止,，然后開(kāi)始運(yùn)動(dòng)至1 600 s,，最后逐步靜止至測(cè)試結(jié)束。三種解算方法都可以較好地進(jìn)行定位解算,。為了更好地分析定位結(jié)果,，畫(huà)出圖 1中的XYZ三維坐標(biāo)上的定位誤差的均方根，如圖 2所示,。

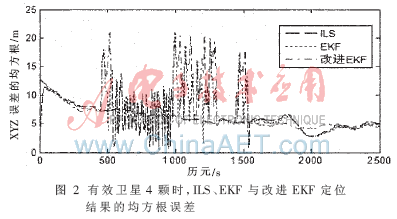
　為了更好地比較ILS,、普通EKF與改進(jìn)EKF算法，計(jì)算圖 2中三種算法在XYZ三個(gè)坐標(biāo)方向上的定位結(jié)果的均方根誤差的平均值,，如表1所示,。

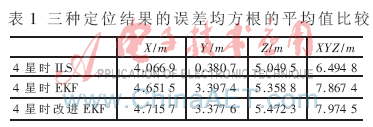
　從圖2和表1可以更清晰地看出，在有效衛(wèi)星不少于4顆時(shí),，三種算法在以ECEF坐標(biāo)系表示的XYZ方向上的定位誤差的均方根均不超過(guò)20 m,，平均定位誤差不超過(guò)10 m,，定位解算精度都很好。其中改進(jìn)的EKF與普通EKF定位精度相當(dāng),，而ILS的定位均方根誤差抖動(dòng)很小,。這是因?yàn)椋慨?dāng)有新的測(cè)量數(shù)據(jù)時(shí),，ILS算法都會(huì)經(jīng)過(guò)多次迭代計(jì)算直至結(jié)果收斂,，而EKF與改進(jìn)的EKF算法均只是利用新息進(jìn)行一次計(jì)算，計(jì)算量要遠(yuǎn)遠(yuǎn)小于ILS,，故而定位結(jié)果會(huì)稍有抖動(dòng),。
3.2 有效衛(wèi)星數(shù)只有3顆時(shí)的定位結(jié)果
　在有效衛(wèi)星數(shù)只有3顆時(shí)，ILS無(wú)法進(jìn)行定位,。分別使用普通EKF和改進(jìn)的EKF算法進(jìn)行定位,，得到在ECEF坐標(biāo)系下的XYZ三維坐標(biāo)上的定位結(jié)果,如圖 3所示。

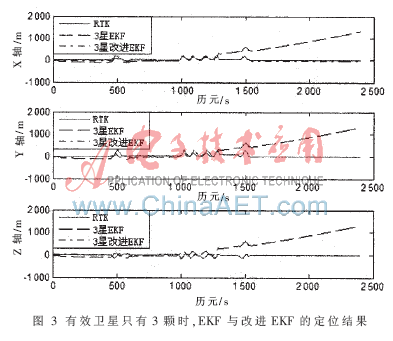
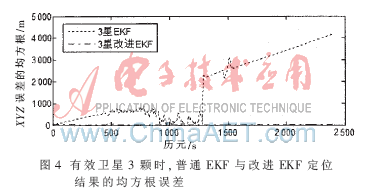
   為了更好地分析定位結(jié)果,，畫(huà)出圖 3中的XYZ三維坐標(biāo)上的定位誤差的均方根,，如圖 4所示。
　為了更好地比較普通EKF算法與改進(jìn)EKF算法,，計(jì)算圖 3中兩種算法XYZ三維坐標(biāo)上的定位結(jié)果的均方根誤差的平均值,，如表 2所示。

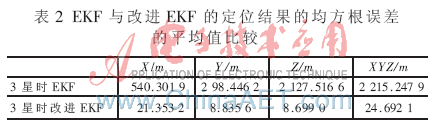
　由圖 3,、圖 4和表 2可知,，在只有3顆有效衛(wèi)星的情況下，普通EKF的定位結(jié)果會(huì)出現(xiàn)明顯的偏移,，而本文提出的改進(jìn)的EKF算法的定位結(jié)果與參考軌跡擬合得很好,，各個(gè)方向上的平均定位誤差均不超過(guò)10 m，定位精度很好,。這說(shuō)明本文提出的改進(jìn)EKF算法在只有3顆有效衛(wèi)星時(shí),，極大地提高了EKF的定位精度。與理論結(jié)果吻合,。

3.3 有效衛(wèi)星為3顆時(shí)改進(jìn)EKF與有效衛(wèi)星為4顆時(shí)普通EKF 的定位結(jié)果
　為了進(jìn)一步分析改進(jìn)EKF算法的性能,，將改進(jìn)EKF算法在只有3顆有效衛(wèi)星時(shí)的定位誤差與普通EKF算法在有4顆有效衛(wèi)星時(shí)的定位誤差進(jìn)行比較，如圖 5所示,。

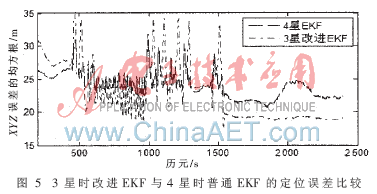
   計(jì)算圖 5中的兩種情況下XYZ三維坐標(biāo)上的平均誤差的均方根,，如表3所示。

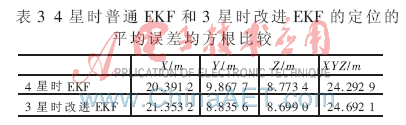
　由圖 5和表 3可知,，在只有3顆有效衛(wèi)星時(shí),，本文提出的改進(jìn)EKF算法所增加的先驗(yàn)信息與增加一顆衛(wèi)星的測(cè)量信息的效果基本一致。故而說(shuō)明在出現(xiàn)GPS信號(hào)阻塞的情況下,，只有3顆有效衛(wèi)星時(shí),，此改進(jìn)EKF算法的定位解算精度非常好。
　綜上所述,，利用實(shí)測(cè)的衛(wèi)星數(shù)據(jù)進(jìn)行驗(yàn)證,，結(jié)果表明：在3顆有效衛(wèi)星的情況下，在靜止?fàn)顟B(tài)和車(chē)載狀態(tài)下,，改進(jìn)的EKF算法的定位精度均明顯優(yōu)于普通的EKF,，且與4顆有效衛(wèi)星時(shí)EKF的定位精度相當(dāng)；在不少于4顆有效衛(wèi)星的情況下,，在靜止?fàn)顟B(tài)和車(chē)載狀態(tài)下,，改進(jìn)EKF算法的定位精度與普通EKF相當(dāng)。由此說(shuō)明,，本文提出增加的先驗(yàn)信息在已有足夠測(cè)量信息時(shí),，并不會(huì)影響定位精度，而只有在3顆有效衛(wèi)星時(shí),，測(cè)量信息對(duì)于定位精度的改進(jìn)與一顆有效衛(wèi)星的測(cè)量信息效果基本一致,，從而大大提高了EKF算法的魯棒性。
    本文在GPS信號(hào)出現(xiàn)阻塞,，有效衛(wèi)星數(shù)降為只有3顆時(shí),，改進(jìn)EKF算法以提高GPS定位解算精度，并使用真實(shí)衛(wèi)星數(shù)據(jù)對(duì)改進(jìn)的EKF算法進(jìn)行了驗(yàn)證,。實(shí)驗(yàn)結(jié)果表明,，在有效衛(wèi)星不少于4顆時(shí)，本文提出的改進(jìn)EKF的定位精度與EKF相當(dāng),。在GPS信號(hào)阻塞,，有效衛(wèi)星數(shù)只有3顆時(shí)，改進(jìn)EKF的定位精度明顯優(yōu)于普通EKF,，且與4顆有效衛(wèi)星時(shí)EKF的定位精度相當(dāng),。受本文算法改進(jìn)中所引入的先驗(yàn)信息的限制，本文提出的改進(jìn)EKF算法適合車(chē)載等地面運(yùn)用,，不適合在垂直地面方向上高速運(yùn)動(dòng)的情形,。
參考文獻(xiàn)
[1]  COOPER S, DURRANT W H F. A kalman filter model for GPS Navigation of Land Vehicles, IEEE Conference on    Intelligent Robots and System(IROS’94),Munich,Germany, 1994(11):12-16.
[2]  MISRA P, ENGE P著.全球定位系統(tǒng)——信號(hào)、測(cè)量與性能(第二版).羅鳴,曹沖,肖雄兵,等譯. 北京：電子工業(yè)出版社,，2008：103-106.
[3]  AGOGINO A, ALAG S, GOEBEL K. Intelligent sensor  validation and sensor fusion for reliability and safety  enhancement in vehicle control, MOU132, UCB-ITSPRR-95-40, California PATH Ressarch Report, 1995.
[4]  KEE C, PARKINSON B W. Wide area differential GPS. Navigation: Journal of The Institute of Navigation.1991,38 (2).
[5]  曹潔,文如泉.非線性濾波算法在機(jī)動(dòng)目標(biāo)跟蹤中的研究[J].信息化縱橫,，2009,28(18):61-64.