1 引 言

　　光纖通訊技術(shù)的飛速發(fā)展使得目前高速通訊網(wǎng)絡(luò)性能的瓶頸集中在高速交換系統(tǒng),，研究,、設(shè)計(jì)和制造高速交換系統(tǒng)對(duì)目前高速通訊網(wǎng)絡(luò)具有極其重要的意義。而且隨著電信網(wǎng)和計(jì)算機(jī)網(wǎng)絡(luò)的高速發(fā)展,，高速大容量的交叉連接或交換設(shè)備和芯片的性能也在大幅度的提高。同時(shí)由于現(xiàn)在的交換機(jī)在不停地更新?lián)Q代,，對(duì)新的交換算法的需求也在不斷增加,。

　　本文的研究工作旨在利用矩陣置換的思想，模擬開發(fā)一種基于T(時(shí)分)-S(空分)-T(時(shí)分)交換網(wǎng)絡(luò)的調(diào)度算法,。提出一種新的三級(jí)交換的矩陣模型,，并在這種模型上設(shè)計(jì)相應(yīng)的無(wú)阻塞交換" title="無(wú)阻塞交換">無(wú)阻塞交換算法。利用矩陣作為數(shù)學(xué)模型,，可以利用矩陣的置換操作搜索交換的設(shè)置,。算法設(shè)計(jì)和實(shí)現(xiàn)的過(guò)程中，大量的實(shí)驗(yàn)表明,，本算法具有良好的特性,，而且通過(guò)芯片級(jí)聯(lián)可實(shí)現(xiàn)。

　　本算法不同于以往的基于圖論的尋徑調(diào)度算法,，力圖通過(guò)對(duì)這個(gè)算法的研究,，為未來(lái)的大型綜合數(shù)字交換網(wǎng)絡(luò)奠定理論和實(shí)踐基礎(chǔ)，并為變化多端的網(wǎng)絡(luò)環(huán)境下快速建立有保障的網(wǎng)絡(luò)服務(wù)提供先期的技術(shù)研究,。

　　2 T-S-T數(shù)字交換網(wǎng)絡(luò)結(jié)構(gòu)

　　典型的T-S-T數(shù)字交換網(wǎng)絡(luò)可以用圖1的模型描述,。

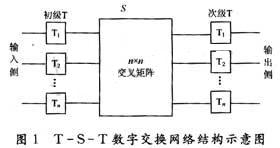
　　整個(gè)交換網(wǎng)絡(luò)以S接線器為核心組織。對(duì)于一個(gè)具有N條輸入復(fù)用線和N條輸出復(fù)用線的交換網(wǎng)絡(luò)而言,，需要配置2N套T接線器,，其中N套在輸入側(cè),，為初級(jí)T接線器，完成用戶的發(fā)送時(shí)隙到交換網(wǎng)絡(luò)內(nèi)部的公共時(shí)隙的交換,；N套在輸出側(cè),，稱為次級(jí)T接線器，完成將交換網(wǎng)絡(luò)內(nèi)部的公共時(shí)隙上的住處傳送到另一用戶的接收時(shí)隙上,。因此,，交換網(wǎng)絡(luò)內(nèi)部提供的公共時(shí)隙的數(shù)量就決定了交換網(wǎng)絡(luò)中能夠形成的話音通路的數(shù)量。中間的S接線器主要由一個(gè)N×N的交叉接點(diǎn)和具有N個(gè)存儲(chǔ)器的控制存儲(chǔ)器組來(lái)組成,，用來(lái)完成將交換網(wǎng)絡(luò)內(nèi)部運(yùn)載的用戶信息從一條輸入側(cè)復(fù)用線上交換到規(guī)定的一條輸出復(fù)用線上,。

　　3 T-S-T交換網(wǎng)絡(luò)數(shù)學(xué)模型的建立

　　3.1 問(wèn)題的描述

　　在建立T-S-T交換網(wǎng)絡(luò)的數(shù)學(xué)模型之前，首先給出這樣的數(shù)學(xué)抽象：用1個(gè)n×n的輸入矩陣inport表示輸入數(shù)據(jù)流,，每一行代表1個(gè)T-S-T交換網(wǎng)絡(luò)的輸入鏈路,，也就是說(shuō)每一行代表l根鏈路HW，每一行內(nèi)元素的位置代表1個(gè)時(shí)隙內(nèi)各個(gè)數(shù)據(jù)幀的次序關(guān)系,。由于T交換是對(duì)同一根鏈路的不同時(shí)隙之間進(jìn)行的交換,，故將其抽象為矩陣的行內(nèi)置換。因此當(dāng)輸入矩陣inport經(jīng)過(guò)一級(jí)T交換后,，得到1個(gè)中間矩陣after_t1,，此矩陣是inport矩陣通過(guò)每一行數(shù)據(jù)的行內(nèi)變換得到。同理,，由于S交換是在不同鏈路的相同時(shí)隙之間進(jìn)行的交換,，類似于對(duì)一個(gè)矩陣在其同一列內(nèi)進(jìn)行列內(nèi)變換，稱其為列內(nèi)置換,。這樣當(dāng) after_tl又經(jīng)過(guò)S交換,，得到另外一個(gè)中間矩陣after_s，此矩陣是after_tl矩陣通過(guò)列內(nèi)變換得到的,。最后,，又經(jīng)過(guò)第二級(jí)的T交換，產(chǎn)生outport矩陣,，類似地,，他是after_s矩陣通過(guò)行內(nèi)變換得到。于是,，可以將交換算法這樣描述：對(duì)于初始矩陣inport,，怎樣能找到一種滿足 T-S-T三級(jí)交換的變換方式，最終得到1個(gè)輸出矩陣outport,。而且對(duì)于用戶要求的任意outport(此矩陣與inport是單播關(guān)系),，都可以通過(guò)算法找到其變換方式，即可以找到2個(gè)中間矩陣。

　　3.2 矩陣模型的建立

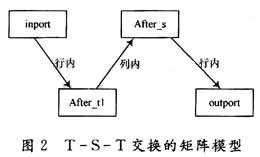
　　將T變換對(duì)應(yīng)于矩陣的行內(nèi)變換,，而S變換對(duì)應(yīng)于矩陣的列內(nèi)變換,，這樣上面的這一段敘述就可以描述為inport矩陣經(jīng)過(guò)一系列的行內(nèi)變換得到after_t1矩陣，after_t1矩陣經(jīng)過(guò)一系列的列內(nèi)變換得到after_s矩陣,，after_s矩陣又經(jīng)過(guò)一系列的行內(nèi)變換得到outport矩陣如圖2所示,。

　　4 交換算法的設(shè)計(jì)思想

　　從上面論述可以看到，本文已經(jīng)將具體的路徑選擇問(wèn)題,，抽象成純粹的數(shù)學(xué)問(wèn)題,。接下來(lái)，本文將從純數(shù)學(xué)的角度來(lái)找出一種算法,，從而解決這個(gè)交換問(wèn)題,。

　　4.1 問(wèn)題的數(shù)學(xué)分析

　　觀察從輸入矩陣inport→中間矩陣after_t1→中間矩陣after_s→輸出矩陣outport整個(gè)的變換過(guò)程，輸入矩陣先后經(jīng)過(guò)2次時(shí)間變換,，而只經(jīng)過(guò)1次空間變換,。也就是說(shuō)，當(dāng)輸入矩陣inport中的某個(gè)元素,，要發(fā)生列變換時(shí),，他只有1次變換機(jī)會(huì)，此情況對(duì)于inport中的任意一個(gè)元素都是適用的,。所以,，時(shí)間變換只起到調(diào)整作用，因此本文要重點(diǎn)考察空間變換,，試圖從空間變換S變換中找出矩陣的特點(diǎn),。

　　不難發(fā)現(xiàn)，中間矩陣 after_s(n×m)(一般情況下,，本文取m=n，無(wú)阻塞的交換網(wǎng)絡(luò))有這樣的特點(diǎn)：每一列的n個(gè)元素,，他們的行號(hào)包含從1～n的所有行號(hào),。如上面的例子可以看到這一點(diǎn)。這樣,，將after_s矩陣經(jīng)過(guò)1個(gè)空間變換,，向空間變換的反方向變換的時(shí)候，這n個(gè)元素就會(huì)回到在inport矩陣原來(lái)的行上,，在經(jīng)過(guò)1個(gè)時(shí)間變換的反變換就可以變成為輸入矩陣inport,。

 　　在發(fā)現(xiàn)中間矩陣after_s的特點(diǎn)之后，就有了基本的思路,。這里的算法只要能夠使得outport矩陣經(jīng)過(guò)1個(gè)時(shí)間變換的反變換后能夠變成為滿足中間矩陣after_s的特點(diǎn)的矩陣,，那么，也就找到一種矩陣的變換方式。解決了這個(gè)交換問(wèn)題,。有沒(méi)有一個(gè)從inport到outport的變換的問(wèn)題,，轉(zhuǎn)換成能不能找到一個(gè)滿足after_s矩陣要求的問(wèn)題，此after_s矩陣只是 outport矩陣經(jīng)過(guò)一個(gè)時(shí)間變換得到,。

 　　這樣,，對(duì)于任意輸入矩陣inpott，經(jīng)過(guò)矩陣的行內(nèi),、列內(nèi),、行內(nèi)3次變換可以得到任意輸出矩陣 outport，從而成功的完成了T-S-T交換,。本文為了方便描述inport和T-S-T交換的核心算法,，不妨將inport定義為順序矩陣n×n，就是以行為序,，從0～n×n-1,，例如n=4，inport被定義為：

　　而outport將是inport的任意置換矩陣,。在這里也不妨將outport假設(shè)為：

　　為了從inport矩陣變換到outport矩陣,，必須找到兩個(gè)中間矩陣after_t1和after_s，從而完成交換路徑的接續(xù),。因此本文的目標(biāo)是研究一種算法,，根據(jù)輸入矩陣和輸出矩陣產(chǎn)生這兩個(gè)中間矩陣，從而使處理機(jī)可以根據(jù)4個(gè)矩陣往寄存器陣列中填值,，這樣就可以實(shí)現(xiàn)T-S-T網(wǎng)絡(luò)交換,。為了以后敘述方便，3個(gè)寄存器陣列定義為：Tregister1(時(shí)分),、Sregister(空分),、Tregister2(時(shí)分)。

　　由于在實(shí)際的 T-S-T交換中,，CPU根據(jù)各個(gè)控制寄存器中的值來(lái)完成交換,。由交換的特點(diǎn)可知，每個(gè)控制寄存器的值是由輸入序列和輸出序列決定的,。其中 Tregisterl的值可以由inport和after_t1決定,，同理，Sregister的值由after_t1和after_s決定,，Tregister2的值由after_s和outport決定,。

　　4.2 算法思想的設(shè)計(jì)

　　算法設(shè)計(jì)要求：

　　(1)對(duì)于任意給定的輸入矩陣和輸出矩陣，都能夠得到2個(gè)中間矩陣,；

　　(2)由輸入矩陣到第一個(gè)中間矩陣只能經(jīng)過(guò)一系列行內(nèi)置換,；

　　(3)由第一個(gè)中間矩陣到第二個(gè)中間矩陣只能經(jīng)過(guò)一系列列內(nèi)置換；

　　(4)由第二個(gè)中間矩陣到輸出矩陣只能經(jīng)過(guò)一系列行內(nèi)置換。

　　由行內(nèi)變換和列內(nèi)變換的性質(zhì)可以推斷出after_t1(AT)和after_s(AS)矩陣的特點(diǎn)如下：

　　AT的特點(diǎn)：ATij=INij'(只能在同一行上進(jìn)行置換),；AS的特點(diǎn)：AS是inport的一個(gè)置換矩陣,；AS的同一列上不可能出現(xiàn)inport同一行上的元素。

　　這是由于AT同一列上不可能出現(xiàn)inport同一行上的元素,，而AT到AS經(jīng)過(guò)的是列內(nèi)變換,。

　　現(xiàn)在有了inport和outport，目標(biāo)是通過(guò)這2個(gè)矩陣找到after_t1和after_s,。從上面的設(shè)計(jì)要求和模型2個(gè)中間矩陣的特點(diǎn)可以看出,，由inport到outport所經(jīng)過(guò)的置換與由outport到inport所經(jīng)過(guò)的置換是對(duì)稱的，所以由outport到inpott置換所得的2個(gè)中間矩陣也是問(wèn)題的解,。而且inport相對(duì)于output較為確定,，因此為了方便描述和算法實(shí)現(xiàn)，本文采用逆推法,，由outport經(jīng)過(guò)一系列的行內(nèi)變換逆推出after_s,，由after_s經(jīng)過(guò)一系列的列內(nèi)變換逆推出after_t1。很容易發(fā)現(xiàn)從after_s到after_t1只需要一個(gè)簡(jiǎn)單的排序就可以完成,，因此算法的關(guān)鍵是由outport推導(dǎo)after_s,。

　　這樣本文研究的交換網(wǎng)絡(luò)調(diào)度算法要解決的關(guān)鍵問(wèn)題等效后分解為：將一個(gè)任意置換矩陣經(jīng)過(guò)一系列的行內(nèi)變換變成為同一列上不存在輸入矩陣的同一行數(shù)據(jù)的置換矩陣(這是由AS的特點(diǎn)所決定的)。將解決這個(gè)關(guān)鍵問(wèn)題的算法稱為交換網(wǎng)絡(luò)調(diào)度算法的核心算法,。

　　5 關(guān)鍵矩陣算法的思想和步驟

　　5.1 高沖突值行優(yōu)先排列算法

　　一些約定和定義：

　　規(guī)則：矩陣after_s同一列上不存在矩陣inport同一行上的數(shù)據(jù),。

　　那么對(duì)于任一給定輸出矩陣outport(OP)，本算法的任務(wù)是,；根據(jù)“規(guī)則”將outport的每一行元素放到after_s(AS)同行的適當(dāng)位置上,。例如假設(shè)現(xiàn)在開始第i行的排列，也就是說(shuō),，第0行到第i～l行的數(shù)據(jù)已經(jīng)初步放置完畢(考慮到回溯,，所以說(shuō)“初步”)，則前i行的每一列元素的初始矩陣行可以組成1個(gè)一維矩陣,，一共n個(gè)一維矩陣,，定義為垂直行陣v[0]，v[1],。…，v[n一1],；而OP的第i行的所有元素的初始矩陣行又可以組成1 個(gè)一維矩陣(元素的初始矩陣行等于該元素整除矩陣維數(shù)的商),，定義為水平行陣h，數(shù)據(jù)結(jié)構(gòu)如圖3所示：

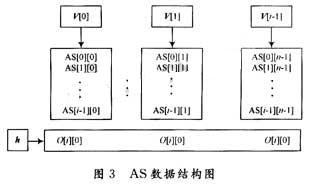
 　　定義：垂直沖突值：vRepeat[n],，其中vRepeat[i](i=0,，1，2，…,，n-1)等于u[i]中的元素在h中的重復(fù)次數(shù)的和,。

　　水平?jīng)_突值：hRepeat[n]，其中hRepcat[i](i=0,，1,，…，n-1)等于k[i]在v中的重復(fù)次數(shù)的和,。

 　　生存數(shù)(lifenum)：假設(shè)vRepeat[j]等于k,，也就是說(shuō)，O[i]中有k個(gè)元素不能放在AS的第j列,，能放在這一列的元素個(gè)數(shù)只有n-k個(gè),，定義為生存數(shù)(lifenum)，將這n-k個(gè)元素下標(biāo)取出形成向量,，定義為生存空間(lifespace)

　　5.2 高沖突值行優(yōu)先排列算法的實(shí)現(xiàn)

　　算法安放數(shù)據(jù)元素時(shí),，首先從vRepeat最大的那一列開始安放hRepeat最大的符合“規(guī)則”的元素，再逐次安放vRepeat中較小的且符合“規(guī)則”的列,。這樣,，大沖突值的元素得到優(yōu)先安放，重排或回溯的可能性就大大減小,。

　　5.2.1 主流程

　　(1)排列第1行數(shù)據(jù),，row=0；

　　(2)row=row+1,，如果row≥n,，則停止，否則轉(zhuǎn)下一步,；

　　(3)統(tǒng)計(jì)沖突值,，調(diào)用判回溯算法判斷是否回溯，如果回溯,，調(diào)用回溯算法,，否則轉(zhuǎn)下一步；

　　(4)選擇vRepeat沖突值最大的列,，根據(jù)“規(guī)則”安放hRepeat中最大的元素,；

　　(5)更新vRepeat和hRepeat；

　　(6)判斷這一行的數(shù)據(jù)是否都安放完畢,，如果是,，轉(zhuǎn)(2)，否則轉(zhuǎn)(3),。

　　5.2.2 判斷回溯算法

　　回溯條件：生存數(shù)為k,，生存空間相同的列的個(gè)數(shù)和大于生存數(shù)k,，則回溯，原因是某生存空間“不夠分配”,。例如,，第i列和第j列(i不等于j)的生存數(shù)都為1和生存空間都為{2}，這樣第2個(gè)元素只能放在一個(gè)位置上,，也就是說(shuō),，無(wú)論如何排列都無(wú)法滿足“規(guī)則”，需要回溯,。

　　定義節(jié)點(diǎn)數(shù)據(jù)結(jié)構(gòu)如圖4所示：

　　判回溯的算法流程：

　　(1)將生存數(shù)相同的所有節(jié)點(diǎn)串成鏈表,，鏈表的序號(hào)等于生存數(shù)；

　　(2)從鏈表序號(hào)為0向鏈表序號(hào)為n順序掃描鏈表,，統(tǒng)計(jì)生存空間相同的節(jié)點(diǎn)個(gè)數(shù),，當(dāng)出現(xiàn)節(jié)點(diǎn)個(gè)數(shù)大于生存數(shù)的情況，需要回溯,，否則轉(zhuǎn)下一步,；

　　(3)將本鏈并入下一個(gè)鏈表；

　　(4)如果所有鏈表都不出現(xiàn)生存空間相同的節(jié)點(diǎn)個(gè)數(shù)和大于生存數(shù)的情況,，則不需要回溯,。

　　5.2.3 回溯算法

　　定義經(jīng)歷表：在回溯過(guò)程中，各元素所“呆過(guò)”的位置序列,。

　　回溯算法流程：

　　(1)確定回溯元素(沖突值最大原則),；

　　(2)為回溯元素找一個(gè)“合法位置”；

　　合法條件：

　　規(guī)則：沖突值小于當(dāng)前情況,；位置不在經(jīng)歷表中,。

　　(3)為其他元素找“合法位置”；

　　6 算法的正確性證明和復(fù)雜度分析

　　從前面的分析可以知道,，要解決整個(gè)交換算法的關(guān)鍵是確定和尋找中間矩陣after_s,，也就是說(shuō)，在解決問(wèn)題之前,，必須確定問(wèn)題有解,。如何確定after_s一定存在，這里可以通過(guò)組合數(shù)學(xué)中的抽屜原理證明必然存在這樣的矩陣,，證明過(guò)程比較簡(jiǎn)單,，本文在這里不做推導(dǎo)證明。

　　從前面的理論分析中知道,，衡量交換算法有2個(gè)重要的指標(biāo)：交換次數(shù)和比較次數(shù),。為了統(tǒng)計(jì)本文所研究的交換算法的性能，本文針對(duì)不同階數(shù)矩陣的交換次數(shù)和比較次數(shù)做了系統(tǒng)的統(tǒng)計(jì)：

　　(1)對(duì)于每一行數(shù)據(jù),，由于統(tǒng)計(jì)沖突值,、判回溯算法和元素的安放算法都是多項(xiàng)式復(fù)雜度，所以,，在不存在回溯的條件下,，本算法是多項(xiàng)式復(fù)雜度。

　　(2)在本算法中,，“沖突”起著非常重要的作用,，本身回避了許多回溯可能。即使回溯,，本行可供回溯元素和非回溯元素“待”的位置個(gè)數(shù)非常有限,，所以元素回溯的空間很小。

　　下面本文給出在不回溯的情況下,，對(duì)高沖突行優(yōu)先排列算法在階數(shù)遞增變化時(shí),，50次平均交換次數(shù)和比較次數(shù)統(tǒng)計(jì)結(jié)果如表1所示。

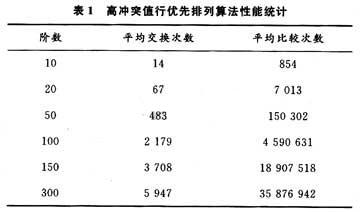
　　從前面對(duì)該算法的描述可知,，該算法通過(guò)使每個(gè)元素“找到”盡可能適合自己的位置,，從而回避了重新排列的許多可能，對(duì)于一行來(lái)說(shuō),，完全避免了全排列,，而且大大減小回溯概率。由于對(duì)大多數(shù)(約80％)矩陣來(lái)說(shuō),，是不會(huì)出現(xiàn)回溯的,，只有類似這樣的矩陣才有可能出現(xiàn)回溯(也可能不回溯)，即,，AS的某些行,，可供選擇的初始行太少。所以,，該算法是一個(gè)近似多項(xiàng)式的算法,，在不回溯的情況下，是多項(xiàng)式算法,。該算法基本上能夠完成交換網(wǎng)絡(luò)的路徑接續(xù),，他有一個(gè)很大的優(yōu)勢(shì)就是在交換過(guò)程中交換的次數(shù)達(dá)到最小，這樣也就大大提高了尋找交換路徑的效率,。本算法具有良好的特性,，而且通過(guò)芯片級(jí)聯(lián)可實(shí)現(xiàn)。