??? 摘 要： 回顧了多分辨率多方向性圖像表示,，分析了其存在的問題,，介紹了新型方向濾波器組" title="濾波器組">濾波器組即均勻方向?yàn)V波器組" title="方向?yàn)V波器組">方向?yàn)V波器組和非均勻方向?yàn)V波器組,，證明了濾波器通帶條件,討論了相關(guān)的設(shè)計(jì)和實(shí)施問題,，并進(jìn)行了實(shí)驗(yàn)仿真,。
??? 關(guān)鍵詞： 方向?yàn)V波器組? 虛自由支撐? 濾波器設(shè)計(jì)
?
??? 在人類視覺系統(tǒng)的研究中,，已證明在人類視覺感知過程中方向信息起到重要作用,。因此，圖像的方向表示將是提取和理解視覺信息的第一步,。景物圖像包含許多集合特征,，如邊緣和紋理，而基于方向基能很好地表示這些特征。另一方面,，在圖像分解中以分層方式用多分辨離散變換表示圖像數(shù)據(jù),，每層均能達(dá)到較好的效果，為由粗分辨率到細(xì)分辨率有效算法的構(gòu)造提供了有利條件,。因此,，多尺度和多方向性是圖像處理的重要特性。
??? 在過去的20年里,，小波" title="小波">小波和濾波器組已經(jīng)有效地運(yùn)用到許多信號處理中,。濾波器組及其應(yīng)用的論題在信號處理領(lǐng)域[１-２]已進(jìn)行了廣泛研究。小波應(yīng)用到圖像處理需要設(shè)計(jì)二維小波基,，這種二維濾波器在逼近點(diǎn)奇異時(shí)（點(diǎn)在一個(gè)圖像中）還有效,，但在逼近線奇異時(shí)（線在圖像中）就無能為力了。這是因?yàn)樾〔◤埩糠e基函數(shù)的同向性不適合處理邊界(或邊緣),。這個(gè)事實(shí)在許多研究中已得到證實(shí),，因此，尋找基于景物圖像較有效的基是當(dāng)前最具吸應(yīng)力的研究領(lǐng)域,。近幾年,，Candes和Donoho構(gòu)建了曲波變換，被證明它是兩變量函數(shù)的一種本質(zhì)上的最佳表示,，除了在非連續(xù)C2（二階可微）曲線，該變換是平滑的,。改進(jìn)的關(guān)鍵是曲波的基函數(shù)遵循類似拋物線的尺度規(guī)則,，使得它能很好地適應(yīng)平滑的邊緣。由于平滑函數(shù)的空間具有C2曲線奇異,，類似于景物圖像具有連續(xù)亮度值和不連續(xù)平滑曲線（邊緣）,，這樣一來，在離散域中尋找同樣的變換變得更為迫切,。Contourlet變換是在2002年由M.N.Do和Martin Vetterli提出的,。二維小波變換僅對零維或不連續(xù)的點(diǎn)有稀疏的表示，而對于輪廓線,，它卻無能為力,。Contourlet變換就是為了克服小波變換的這種不足而提出的，其濾波器結(jié)構(gòu)是拉普拉斯金字塔和方向?yàn)V波器組的聯(lián)合,，不僅具有小波的多分辨率特性和時(shí)頻局域特性,，還具有很強(qiáng)的方向性和各向異性，因此,，它對輪廓等紋理線的表示很稀疏,。因?yàn)閳D像是由很多短的輪廓線組合而成，Contourlet變換對圖像進(jìn)行變換后得到的系數(shù)也要比小波稀疏,。因此,，Contourlet變換能很好地應(yīng)用于圖像的壓縮,、去噪和特征提取。但該變換盡管從方向成分中分離了低頻成分,，而分離過程是在低頻段完成的不具有最大抽樣特性,。針對這一問題，本文介紹一種具有最大抽樣特性的新型方向?yàn)V波器組即均勻方向?yàn)V波器組和非均勻方向?yàn)V波器組,。具體介紹了最大抽樣特性所要滿足的濾波器組的虛自由支撐（可容許性）和兩種新型濾波器組及其設(shè)計(jì)方案,，并進(jìn)行了實(shí)驗(yàn)仿真。
1 濾波器組的虛自由支撐(可容許性)
??? 對于一個(gè)完全重構(gòu)(PR)濾波器組,，要實(shí)現(xiàn)最大抽樣其抽樣矩陣的虛自由支撐特性（AFS）是必須具備的,。如果一個(gè)二維信號x(n)以采樣矩陣M向下采樣，則向下采樣信號y(n)=x(Mn)的離散傅立葉變換[2]是：
??? 
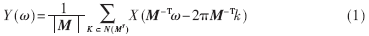
式中,，N(MT)是由矩陣MT產(chǎn)生的屬于對稱平行六面體(SPD)的所有整數(shù)格子點(diǎn)的集合,。
??? 如果濾波器是理想的，又可以證明該濾波器滿足AFS特性,，則濾波器是PR濾波器組,。一個(gè)關(guān)于濾波器通帶條件即當(dāng)抽樣系數(shù)Ｍ抽樣時(shí)沒有混淆現(xiàn)象的定理是：
??? 定理：在[-π，π)2支撐S的區(qū)域稱為關(guān)于矩陣M的AFS,，當(dāng)且僅當(dāng)滿足下列條件：每個(gè)點(diǎn)x∈SPD(πM-T),，存在惟一點(diǎn)y∈S、m∈Z2,，則X-Y=2πM-Tm,。
??? 證明：該定理是濾波器虛自由抽樣理論[2]的推廣，支撐是SPD(πM-T)的復(fù)制轉(zhuǎn)移,。當(dāng)式（1）的主成分和混淆圖像間沒有重疊時(shí),，一個(gè)理想濾波器支撐在區(qū)域S關(guān)于抽樣矩陣Ｍ，滿足其AFS特性,。
??? 假設(shè)式（１）的主項(xiàng)和混淆項(xiàng)間有一個(gè)重疊區(qū)域,，定義區(qū)域S0={MTω|ω∈S}和S1={MTω+2πk|ω∈S，k≠0}是重疊的,，則存在ω0,，ω1∈S有：
??? MTω0=MTω1+2πk?????????????????????????????????????????? (2)
??? 因?yàn)?/FONT>
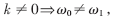由定理，存在惟一的
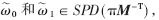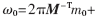
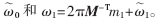分別與ω0和ω1對應(yīng),，則有
由SPD(πMT)映射到S的惟一性,，
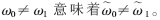由式（2）可得：
??? 
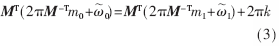
??? 簡而言之：
??? 
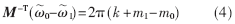
??? 由SPD(πM-T)定義和式(4)，則有(k+m1-m0)∈(-1,，1)2,。但所有的k、m1、m0都屬于整數(shù)格子,，因此(k+m1-m0)＝０,，它使得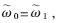
導(dǎo)致矛盾。如果理論條件不滿足,，同理可證明AFS條件將不滿足,。
??? 根據(jù)上述理論，對于一個(gè)任意形狀的關(guān)于矩陣Ｍ的濾波器的一個(gè)簡單虛自由抽樣測試如下：如果能找到一個(gè)支撐形狀濾波器的分區(qū)即存在mk∈Z2,，以便此時(shí)分區(qū)的kth元素被2πM-Tmk所搬移，則分區(qū)搬移集合就擬合在SPD(πM-T),。這里標(biāo)注mk可以不同于分區(qū)的每個(gè)元素,。
2 均勻方向?yàn)V波器組
??? 傳統(tǒng)的DFB和新的DFB對頻域的分割分別如圖1(a)、(b),、(c)所示,。新的頻率分割方法來自于景物圖像的幾何特征。圖像通常有邊緣平滑區(qū)域和紋理平滑區(qū)域,，紋理平滑區(qū)域在一幅圖像中方向高通子帶能提取方向信息,，而低通" title="低通">低通子帶提供一個(gè)粗糙的逼近。
?
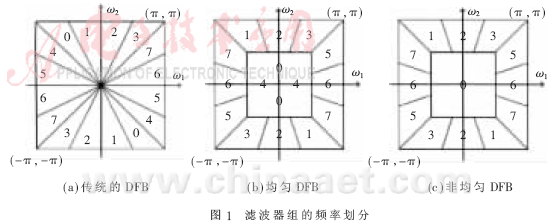
??? 為了實(shí)現(xiàn)圖1(b)中八通道濾波器組的頻率分割,，本文采用了一個(gè)均衡八通道濾波器組,，如圖2(a)所示。該濾波器組稱為均勻方向?yàn)V波器組,該框架有許多優(yōu)點(diǎn)：(1)濾波器設(shè)計(jì)具有高度的規(guī)律性,。(2)整個(gè)八通道濾波器能直接實(shí)施比二進(jìn)制樹更為緊湊的結(jié)構(gòu),。(3)方向子帶中濾波器組無直流泄漏。
?
??? 圖3展示了一個(gè)測試示例,，說明在新的DFB中方向子帶1滿足AFS條件,?？梢钥闯?，一個(gè)兩通道組滿足容許特性。由前述定理說明新的DFB是具有最大抽樣特性的,。
?
?
3 利用非均勻DFB進(jìn)行多分辨率方向分解
??? 利用濾波器組進(jìn)行多分辨率圖像分解,，是按低通系數(shù)重復(fù)同樣的濾波器組。對于一維倍頻帶多分辨率,，低通濾波器的通帶支持(帶寬)是整個(gè)頻率空間的1/2,。因此，二維倍頻帶多分辨率,，低通濾波器的通帶支持(帶寬)是整個(gè)頻率空間的1/4,。均勻DFB有兩個(gè)低頻子帶（0和4），聯(lián)合起來可獲得1/4的采樣因子。一個(gè)最好的方法是使用一個(gè)非均勻?yàn)V波器組,，該濾波器具有1/4采樣因子和采樣矩陣D2的一個(gè)低通成分,，如圖2(b)所示。其他的六個(gè)方向子帶采用相同的方法,。非均勻DFB的頻率劃分如圖1（c）所示,，其優(yōu)點(diǎn)有：類似于DWT有同樣的低通頻率支撐(-π/2，π/2)2,，圖像分解代之以更加精細(xì)的水平,、垂直和對角子帶。非均勻DFB使用了六個(gè)方向子帶,，在分解中提供了更多的靈活性：
??? (1)要獲得一幅圖像的一個(gè)(方向的)多分辨率,，可以將整個(gè)濾波器組在低通通道上重復(fù)。
??? (2)要成倍提高方向解析度,，可以在高通通道的每個(gè)輸出端疊加一個(gè)具有扇形通帶的兩通道濾波器組,。
4 空域優(yōu)化濾波器設(shè)計(jì)
??? 設(shè)計(jì)非分離多分辨率濾波器組是一個(gè)具有挑戰(zhàn)性的問題，通常的方法是變量轉(zhuǎn)換[3-4],?；谝痪SPR濾波器組的二維濾波器設(shè)計(jì)方法" title="設(shè)計(jì)方法">設(shè)計(jì)方法應(yīng)用到兩個(gè)以上通道較為困難。目前,，還沒有系統(tǒng)的方法設(shè)計(jì)具有規(guī)則性和某種頻率特性(阻帶衰減,，通帶波紋等)的二維PR濾波器組。
??? 本文中所用的優(yōu)化設(shè)計(jì)方法在設(shè)計(jì)濾波器時(shí)不使用樹結(jié)構(gòu),。與其他濾波器優(yōu)化設(shè)計(jì)方法不同,，重構(gòu)錯(cuò)誤的計(jì)算即分析和合成濾波器系數(shù)的雙線性函數(shù)是在時(shí)域進(jìn)行的，設(shè)計(jì)過程是計(jì)算過后設(shè)法減少在每步中的重構(gòu)錯(cuò)誤,。該方法只通過解迭代的線性方程組設(shè)計(jì)一個(gè)PR正交或雙正交的濾波器組,，就可以實(shí)現(xiàn)均勻DFB和非均勻DFB兩種情況的濾波器組的設(shè)計(jì)，并且設(shè)計(jì)很靈活,。設(shè)s={1,，2，3,，5,，6，7}是非均勻DFB情況下的方向子帶索引的集合,，子帶數(shù)量M=8,，則該設(shè)計(jì)能夠表示為一個(gè)優(yōu)化問題，其目標(biāo)函數(shù)為：
??? 
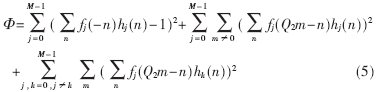
或：
??? 
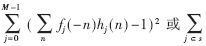
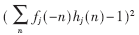??? 式(5)和式(6)分別是均勻DFB和非均勻DFB的目標(biāo)函數(shù),。目標(biāo)函數(shù)主要由兩部分組成,，構(gòu)成了PR或雙正交特性,。其中，第一項(xiàng)
符合歸一化條件,，只有當(dāng)兩個(gè)濾波器
??? 
??? 另外，當(dāng)分析和合成濾波器時(shí)有等同的規(guī)則性度量,，具有下列線性約束[1]：
??? 
式中,，r1、r2是非負(fù)整數(shù),，r1+r2
??? 迭代期間,，每個(gè)濾波器組是相應(yīng)分析濾波器的時(shí)間反轉(zhuǎn),，即fj(n)=hj(-n)，由此可獲得濾波器組的正交性,。為了使濾波器收斂到一個(gè)正交解,，需要更新濾波器系數(shù)，即：
??? 
5 仿真實(shí)驗(yàn)
??? 本次實(shí)驗(yàn)是比較小波和非均勻?yàn)V波器組的逼近性能,，將512×512大小的芭芭拉圖像分解為三層,，低層用DWT，兩個(gè)高層用非均勻DFB對Barbara圖像進(jìn)行分解(該圖像同時(shí)也被“9-7”小波分解),，然后用同樣數(shù)量的最高幅度系數(shù)重構(gòu),，如圖4所示。重構(gòu)圖像使用了6 144個(gè)系數(shù)(整個(gè)圖像系數(shù)的2.3%),，結(jié)果非均勻?yàn)V波器組信噪比略高于小波,，而且可以看出,，前者視覺質(zhì)量要好于后者,。
?
??? 本文介紹了新型DFB即均勻DFB和非均勻DFB，討論了相關(guān)的設(shè)計(jì)和實(shí)施問題,。這兩種DFB可以用于二維信號的多方向多分辨率表示,。根據(jù)樹形結(jié)構(gòu)的頻率特性和規(guī)則性約束設(shè)計(jì)要求,，得到了DFB的直接設(shè)計(jì)方法,在較高的計(jì)算代價(jià)要求下，該方法允許在高通帶設(shè)計(jì)性能較高的方向?yàn)V波器,。該設(shè)計(jì)方法首次給出了多分辨率多方向二維PR濾波器保持最大分樣的特性,，并且用簡單的兩通道濾波器組，方向解析度就能夠得到增加,，簡單的設(shè)計(jì)就服從近似正交DFB,，其設(shè)計(jì)結(jié)果經(jīng)圖像非線性逼近。實(shí)驗(yàn)表明,，該方向?yàn)V波器組具有一定的應(yīng)用潛力,。
參考文獻(xiàn)
[1] VETTERLI M，KOVACEVIC J.Wavelets and subband coding.Prentice Hall,，Englewood Cliffs,，NJ，1995.
[2] VAIDYANATHAN P P.Multirate systems and filter?banks.Prentice-Hall,，Englewood Cliffs,，NJ，1993.
[3] LIM J S.Two-dimensional signal and image processing.Prentice Hall,，Englewood Cliffs,，NJ，1990.
[4] TAY D B H,，KINGSBURY N G.Flexible design of multidimensional perfect reconstruction fir 2-band?filters using transformations of variables. IEEE Transaction on Image Processing,，2(4)：466-480，Oct 1993.