一種基于鏡像原理修正傳感器非線性誤差的方法
摘要： 如何對(duì)傳感器非線性誤差進(jìn)行修正是一個(gè)具有普遍意義的技術(shù)問題。基于鏡像原理對(duì)傳感器的非線性誤差修正提出了一種軟件方法,，該方法克服了目前常用的諸如硬件補(bǔ)償法,、分段直線修正法、人工神經(jīng)網(wǎng)絡(luò)修正法等存在的弊端,，同時(shí)用某霍爾式位移傳感器的標(biāo)定結(jié)果作為例子對(duì)該方法的具體應(yīng)用進(jìn)行了詳細(xì)的論述。事實(shí)證明該方法操作簡(jiǎn)單，修正效率高,，結(jié)果穩(wěn)定可靠。
Abstract：
Key words :
一,、引言
在測(cè)控系統(tǒng)中,，一般采用傳感器對(duì)被測(cè)參數(shù)進(jìn)行拾取和轉(zhuǎn)換。由于大多數(shù)傳感器的輸入/輸出特性是非線性的,，為了提高測(cè)量準(zhǔn)確度,，常需要對(duì)傳感器的非線性誤差進(jìn)行修正，因此,，如何對(duì)傳感器非線性誤差進(jìn)行修正是一個(gè)具有普遍意義的技術(shù)問題,。常用的方法有：
（1）硬件補(bǔ)償法，該方法難以作到全程有效補(bǔ)償,，且存在補(bǔ)償電路硬件漂移等問題,；
（2）分段直線修正法，該方法存在不連續(xù)、不光滑,，對(duì)所標(biāo)定的某些點(diǎn)的依賴性大,，極可能不過零點(diǎn)的弊端；
（3）人工神經(jīng)網(wǎng)絡(luò)修正法,，這是近幾年興起的新方法,。該方法具有使用的樣本數(shù)少、算法較簡(jiǎn)單等優(yōu)點(diǎn),，應(yīng)用前景良好,，但已經(jīng)掌握該技術(shù)的人不特別多，使用推廣受到一定程度的限制,。
因此,，在這里基于最小二乘法[1]并模擬鏡像原理對(duì)傳感器非線性誤差的修正提出了一種新方法。
（1）硬件補(bǔ)償法，該方法難以作到全程有效補(bǔ)償,，且存在補(bǔ)償電路硬件漂移等問題,；
（2）分段直線修正法，該方法存在不連續(xù)、不光滑,，對(duì)所標(biāo)定的某些點(diǎn)的依賴性大,，極可能不過零點(diǎn)的弊端；
（3）人工神經(jīng)網(wǎng)絡(luò)修正法,，這是近幾年興起的新方法,。該方法具有使用的樣本數(shù)少、算法較簡(jiǎn)單等優(yōu)點(diǎn),，應(yīng)用前景良好,，但已經(jīng)掌握該技術(shù)的人不特別多，使用推廣受到一定程度的限制,。
因此,，在這里基于最小二乘法[1]并模擬鏡像原理對(duì)傳感器非線性誤差的修正提出了一種新方法。
二,、非線性誤差修正的鏡像原理
設(shè)P（i=,，2，....n為P（Yi﹒Y（Y﹒Y不但連續(xù),，而且必過零點(diǎn),，甚至可以高階光滑，這正是我們所期望的結(jié)果,。）對(duì)輸出Y有效地發(fā)揮著“興小衰大”的動(dòng)態(tài)調(diào)節(jié)作用,，而修正曲線z=f(Y)。顯然,，鏡像曲線y=f）相乘就得到了傳感器的非線性誤差修正曲線z=f(Y)點(diǎn)關(guān)于直線Y=X的一類特殊的鏡像,。顯然，如果P點(diǎn)在直線Y=X上方偏離該直線越遠(yuǎn),，即其縱坐標(biāo)越大,，則鏡像點(diǎn)Q在該直線下方偏離它也越遠(yuǎn)，即其縱坐標(biāo)越小,，反之亦然,。如果將P點(diǎn)的縱坐標(biāo)Yi與鏡像點(diǎn)Q的縱坐標(biāo)Xi/ Yi相乘，不難發(fā)現(xiàn)該乘積就成了輸入值Xi,。因此,，將傳感器的輸出曲線即P點(diǎn)所在的曲線Y與其鏡像曲線即鏡像點(diǎn)Q所在的曲線y=f）為傳感器標(biāo)定時(shí)得到的一系列點(diǎn)，設(shè)點(diǎn)Q（Yi,，Xi/Yi）1（Xi,，Yi）
三、非線性誤差修正方法
（1）設(shè)點(diǎn)P為傳感器標(biāo)定時(shí)得到的足夠多個(gè)離散點(diǎn),，其中Xi0,，i=,，2，...
（2）采用描點(diǎn)法描出點(diǎn) P關(guān)于直線Y=X,，根據(jù)鏡像點(diǎn)的分布情形設(shè)的鏡像點(diǎn)Q（Yi,，Xi/Yi）（Xi，Yi）,，n（下同）。1為標(biāo)準(zhǔn)輸入,，Yi為對(duì)應(yīng)的輸出值,，且Yi≠（Xi，Yi）
（2）采用描點(diǎn)法描出點(diǎn) P關(guān)于直線Y=X,，根據(jù)鏡像點(diǎn)的分布情形設(shè)的鏡像點(diǎn)Q（Yi,，Xi/Yi）（Xi，Yi）,，n（下同）。1為標(biāo)準(zhǔn)輸入,，Yi為對(duì)應(yīng)的輸出值,，且Yi≠（Xi，Yi）
計(jì)鏡像曲線y=f（Y
（3）用最小二乘法擬合曲線的原理求出y的待定系數(shù)即確定了鏡像點(diǎn)Q所在的鏡像曲線,。
（4）將y與傳感器輸出Y,。相乘即得到非線性誤差修正曲線z(Y)=y(Y)Y(Y)(Yi，Xi/Yi)(Y)）的合適形式,。在其定義域內(nèi),，該曲線可以是多項(xiàng)式、指數(shù)函數(shù),、對(duì)數(shù)函數(shù),、冪函數(shù)等，甚至可以是它們的任意組合形式,。（Y）
（3）用最小二乘法擬合曲線的原理求出y的待定系數(shù)即確定了鏡像點(diǎn)Q所在的鏡像曲線,。
（4）將y與傳感器輸出Y,。相乘即得到非線性誤差修正曲線z(Y)=y(Y)Y(Y)(Yi，Xi/Yi)(Y)）的合適形式,。在其定義域內(nèi),，該曲線可以是多項(xiàng)式、指數(shù)函數(shù),、對(duì)數(shù)函數(shù),、冪函數(shù)等，甚至可以是它們的任意組合形式,。（Y）
四,、非線性誤差修正實(shí)例
因任何一個(gè)初等函數(shù)均可以用一個(gè)適當(dāng)?shù)?/span>k/輸出特性為準(zhǔn)線性，且較難準(zhǔn)確判斷鏡像點(diǎn)Q的鏡像曲線y的合適形式時(shí),，其鏡像曲線可設(shè)為一個(gè)標(biāo)準(zhǔn)的多項(xiàng)式,，其次數(shù)k可根據(jù)需要人為或由計(jì)算機(jī)根據(jù)非線性誤差限等自動(dòng)確定，但應(yīng)滿足k≤n+1,。
(Y)=f(Y)（Yi,，Xi/Yi）次多項(xiàng)式去充分逼近它，當(dāng)傳感器的輸入
(Y)=f(Y)（Yi,，Xi/Yi）次多項(xiàng)式去充分逼近它，當(dāng)傳感器的輸入
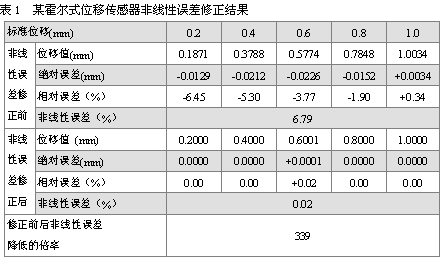
這里以表1中所示的某霍爾式位移傳感器標(biāo)定數(shù)據(jù)[2]/輸出特性為準(zhǔn)線性的,，可設(shè)鏡像點(diǎn)Q的鏡像曲線為一個(gè)三次多項(xiàng)式,，即：（Yi，Xi/ Yi）為例來說明非線性誤差修正的具體方法,?；谄漭斎?/span>
（1）
由表1數(shù)據(jù)，并根據(jù)上文所述非線性誤差修正方法可得到標(biāo)定點(diǎn)（0.2, 0.1871）,、（0.4, 0.3788）,、（0.6, 0.5774）、（0.8, 0.7848）,、（1.0, 1.0034）對(duì)應(yīng)的鏡像點(diǎn)為（0.1871, 0.2/0.1871）,、（ 0.3788,， 0.4/0.3788）、（0.5774,，0.6/0.5774）,、（0.7848, 0.8/0.7848）、（1.0034,，1.0/1.0034）,。這些鏡像點(diǎn)所在的鏡像曲線的待定系數(shù)可根據(jù)第三條借助計(jì)算機(jī)求得，即：
aa´10-2;a´10-2 a´10-23=1.828396904320512=-6.150873642483691=-3.787355198643510=1.07808300655524
故所求得的鏡像曲線為：
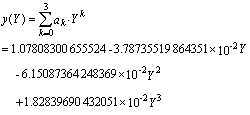2）（
故所求得的非線性誤差修正曲線方程為：
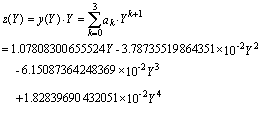3）（
參數(shù)Y代表Y(含所帶的正負(fù)符號(hào))的最大值與最小值之差,。由表1知,，采用本方法經(jīng)軟件修正后，傳感器非線性誤差由原來的6.79%降低到0.02%,，即降低了近339倍,，可見修正結(jié)果非常理想。的修正值,。位移值的非線性誤差等于在整個(gè)標(biāo)定范圍內(nèi)其相對(duì)誤差代表傳感器的位移輸出值,，z(Y)
五、結(jié)束語(yǔ)
理論分析和事實(shí)表明,，該修正方法原理簡(jiǎn)單,，修正效率高，結(jié)果穩(wěn)定可靠,。不難看出,，鏡像曲線y的形式設(shè)計(jì)是否合理，是決定修正效果的關(guān)鍵因素,，如果遇到修正后非線性誤差不太理想的情況,，則說明我們?cè)谏衔乃龇蔷€性誤差修正方法部分設(shè)計(jì)的鏡像曲線的形式不太合理，即鏡像曲線本身應(yīng)該有“拐點(diǎn)”而我們?cè)谠O(shè)計(jì)鏡像曲線時(shí)卻忽視了,。
此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載。