足球機器人系統(tǒng)是一個典型的且非常具有挑戰(zhàn)性的多智能體系統(tǒng),。在足球機器人比賽中，路徑規(guī)劃的主要目的是在充滿對抗的賽場上規(guī)劃出一條滿足某項評價指標(biāo)的無碰撞路徑,。路徑規(guī)劃主要應(yīng)用于機器人底層策略中,。作為足球機器人基本動作實現(xiàn)的基礎(chǔ)，路徑規(guī)劃的優(yōu)劣將直接影響動作的實時性和準(zhǔn)確性,。因此,，每個足球機器人研究者都把它作為一個研究重點。全局路徑規(guī)劃一般包括環(huán)境建模和搜索策略2個子問題,。其中環(huán)境建模的主要方法有：可視圖法,、自由空間法和柵格法^[1]等。目前常用的搜索技術(shù)有：梯度法^[4][5],、 A*等圖搜索方法,、枚舉法和隨機搜索法等。而這些方法也存在一些問題：梯度法易陷入局部最小點,，圖搜索方法和枚舉法不能用于高維的優(yōu)化問題,，隨機搜索法計算效率太低。本文將基于小生境的遺傳算法用于足球機器人路徑規(guī)劃中,，改進了傳統(tǒng)算法的性能,同時具有很高的全局尋優(yōu)能力和收斂速度,，同時可進一步提高解的精度。
1 小生境遺傳算法^[2][6]
　　在自然界中,，特征,、性狀相似的物種往往相聚在一起，并在同劣種交配繁衍后代,。在基本的遺傳算法(SGA)中,，交配完全是隨機的，雖然這種隨機化的雜交形式在尋優(yōu)的初級階段保持了解的多樣性,，但在進化的后期,，大量個體集中于某一極值點上，它們的后代造成了近親繁殖,。遺傳算法由于其強大的全局搜索能力,，求解多峰值函數(shù)的優(yōu)化計算時，一般只能找到個別的幾個最優(yōu)解,，甚至得到的是局部最優(yōu)解,；由于搜索的隨機性，因而解的精度不高,。為了使優(yōu)化算法能夠找到全部的最優(yōu)解,，引進小生境的概念。
　　本文使用一種可標(biāo)記進化方向的小生境遺傳算法DRN-GA(Direction Record Niche Genetic Algorithm)，特點是：基于“分享機制”更好地保持解的多樣性,，同時具有很高的全局尋優(yōu)能力和收斂速度,；利用進化過程中的有用信息，為每個個體標(biāo)記進化方向,。執(zhí)行DRN-GA算法后,，若以每個個體為初始點，按標(biāo)記的進化方向繼續(xù)局部尋優(yōu),，會進一步提高解的精度,。
1.1 個體編碼結(jié)構(gòu)
　　個體編碼中除應(yīng)包含決策變量的編碼外，還要有記憶進化方向的部分,。為適應(yīng)本算法,，設(shè)計個體編碼方案如下示：

1.2 小生境實現(xiàn)原理及適應(yīng)度函數(shù)的確立
　　小生境技術(shù)就是將每一代個體劃分為若干類，每類中選出若干適應(yīng)度較大的個體作為一個類的優(yōu)秀代表組成一個種群,，再在種群中以及不同種群之間通過雜交,、變異產(chǎn)生新一代個體群，同時采用預(yù)選擇機制,、排擠機制或分享機制完成選擇操作,。基于這種小生境技術(shù)的遺傳算法NGA(Niched Genetic Alogorithm)可以更好地保持解的多樣性,，同時具有很高的全局尋優(yōu)能力和收斂速度,，特別適用于復(fù)雜多峰函數(shù)的優(yōu)化問題。
　　在普通遺傳算法的進化過程中,，每一代進行選擇,、交叉、編譯操作之前加入如下操作：通過個體之間的相似程度的共享函數(shù)調(diào)整群體中個體的適應(yīng)度,，從而在群體的進化過程中,，算法能依據(jù)該調(diào)整后的新適應(yīng)度進行選擇操作，以維護群體的多樣性,，創(chuàng)造出小生境的進化環(huán)境。共享函數(shù)是表示群體中兩個個體之間密切關(guān)系程度的一個函數(shù),，可記為S(d_ij),，其中d_ij表示個體i和個體j之間的某種關(guān)系。適應(yīng)度共享函數(shù)的直接目的是將搜索空間的多個不同峰值在地理上區(qū)分開來,，每個峰值處接受一定比例數(shù)目的個體,，比例大小與峰值高度有關(guān)。為實現(xiàn)這樣的分布,，共享法將個體的目標(biāo)適應(yīng)度降低,，即適應(yīng)度值f_i除以一個niche計數(shù)m_i獲得共享函數(shù)，niche計數(shù)m_i作為個體鄰集密集程度的估計。m_i=其中,，d[i,，j]是個體i和j的距離，Sh[d]是共享函數(shù),，此函數(shù)遞減,，Sh[0]=1和Sh[d≥σ_share]=0。
　　采用一種將海明距離測度(基因型差異)與適應(yīng)度距離(表現(xiàn)型差異)相結(jié)合的方法,。若d₁(x_i,，x_j)為任意兩個個體x_i和x_j的海明距離，d₂(x_i,，x_j)是適應(yīng)度距離,，這時共享函數(shù)可定義為：
　　
　　其中，σ₁和σ₂是niche的半徑,，即分別為基因型和表現(xiàn)型的作為一個niche內(nèi)的個體最大距離,。個體的適應(yīng)度函數(shù)在共享后變?yōu)槿缦滦问剑?BR>　　
1.3 進化方向的確立
　　設(shè)單變量函數(shù)y=g(x)，且x₁-x₂〈ρ,，ρ為一較小正數(shù),。設(shè)目標(biāo)函數(shù)為J=max[g(x)]。進化示意圖如圖1所示,。由圖1知,，x₁比x₂更優(yōu)。根據(jù)x₁〈x₂,，g(x₁)〉g(x₂)及x₁-x₂〈ρ可知,，在x₁的一個鄰域內(nèi)g(x)是下降的，可推出,，存在一很小正數(shù)ε,，使得g(x₁-ε)〉g(x₁)，即x₁-ε比x₁更優(yōu)的點,，所以x₁的進化方向為-1,。

2 小生境遺傳操作步驟
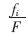　　小生境遺傳操作步驟：(1)根據(jù)編碼方案，把路徑點編碼成位串形式,，轉(zhuǎn)化為染色體(路徑),。(2)選擇合適的參數(shù)：群體的大小(所含個體數(shù)目)、交叉概率P_c和變異概率P_m,。(3)隨機產(chǎn)生一個初始群體即N條路徑,。(4)根據(jù)適應(yīng)值函數(shù)計算每條路徑的適應(yīng)值f(p_i(t))，為適應(yīng)度較大者標(biāo)記進化方向,，根據(jù)個體的適應(yīng)度按比例選擇N個個體,。(5)選擇：計算每一條路徑的選擇概率P=及累計概率q_i=∑p_j,，j=1，…,，i,。(6)交叉：對每條路徑產(chǎn)生[0，1]間隨機數(shù)r,，如果r〈P_c,則該條路徑參加交叉操作,，如此選出參加交叉的一組路徑后，隨機配對,；對每一對,，產(chǎn)生[0，1]間的隨機數(shù)以確定交叉的位置,。(7)變異：如果變異概率為P_m,，則可能變異的位數(shù)的期望值為P·n·N(n為染色體串長，N為群體),。(8)如果新個體數(shù)未達(dá)到M,，則轉(zhuǎn)向第(5)步繼續(xù)進行遺傳操作，否則代數(shù)加1,，d=d+1,；將新群體的M 條路徑的適應(yīng)值由大到小進行排序，保存適應(yīng)值最大的路徑點,；如果d≠g(g是設(shè)定的代數(shù)),，則轉(zhuǎn)向第(4)步，否則選用g代替f中最優(yōu)的路徑上的點,。
3 精確優(yōu)化
　　DRN-GA執(zhí)行后,，得到的種群每個個體中都保存了進化方向。局部尋優(yōu)沿進化方向以步長step尋找更優(yōu)解,， 對每個個體沿進化方向繼續(xù)搜索,，可進一步提高解的精度。兩算法可串行執(zhí)行,。精確優(yōu)化結(jié)構(gòu)示意圖如圖2所示,。

4 仿真
　　算法的搜索能力和優(yōu)化精度在路徑規(guī)劃中的應(yīng)用性能，可以通過下述函數(shù)及其仿真圖形驗證,。函數(shù)精度為0.01,，每個變量所占的二進制編碼長度為9，個體編碼為20位,，種群數(shù)目為100，終止代數(shù)為100,，交叉概率為P_c=0.6,，變異概率P_m=0.002,，運行次數(shù)為40。
　　(1)Gauss函數(shù)
　　選取函數(shù)：
　　f₁(x,，y)=xsin(4πx)-ysin(4πy+π)+1
　　x,，y∈[-1，2],，f₁^*(1.6289,，1.6289)=4.2539
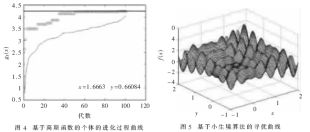
　　采用高斯函數(shù)和基于小生境算法的尋優(yōu)曲線及其個體的進化過程曲線分別如圖3～圖6所示。
　　小生境遺傳算法與基本遺傳算法的性能對比如表1所示,。

　　(2)Chaos-cat mapping函數(shù)^[3]
　　選取函數(shù)：
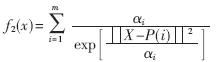　　X是一個兩輸入向量,，[X₁，X₂]∈[0,，100]²,。基于Chaos-cat mapping函數(shù)和小生境算法的尋優(yōu)曲線和個體進化過程曲線分別如圖7～圖10所示,。

?

?

?

　　改進算法與基本遺傳算法的性能對比如表2所示,。