0 引言

    更改條件/判定覆蓋(MC/DC)準(zhǔn)則是一種軟件結(jié)構(gòu)覆蓋性測試準(zhǔn)則,，非常適合大型的軟件測試領(lǐng)域,，如國防、航空航天領(lǐng)域^[1-2],。MC/DC與語句覆蓋,、條件覆蓋、判定覆蓋等比較,，能大幅減少測試用例數(shù),，如測試系統(tǒng)中有10個判定條件時，條件組合覆蓋需要1 024個測試用例,，而MC/DC只需要11~20個測試用例^[3-4],。在國內(nèi)MC/DC最小測試用例集生成算法的相關(guān)研究中，比較典型的是最小真值表法^[5]和快速生成法^[6],，但這兩種算法只適合處理非耦合條件的布爾表達(dá)式,。也有學(xué)者將MC/DC準(zhǔn)則應(yīng)用于帶弱耦合條件和強(qiáng)耦合條件的布爾表達(dá)式中^[7]。本文結(jié)合矩陣方式,，從布爾表達(dá)式的語法二叉樹的葉子節(jié)點(diǎn)依次遞歸至根節(jié)點(diǎn),，直接生成完備的最小化測試用例集。

1 算法相關(guān)描述

    布爾表達(dá)式相關(guān)概念：條件表示不含有布爾操作符號的布爾表達(dá)式，記為P_i(1≤i≤n),。判定表示由條件Pi和若干布爾操作符號所組成的一個布爾表達(dá)式,。

    MC/DC覆蓋準(zhǔn)則^[8]：(1)程序中，每個入口點(diǎn)和出口點(diǎn)至少被調(diào)用1次,；(2)程序中判定的每個條件的所有取值至少出現(xiàn)1次,，且能獨(dú)立影響該判定的輸出；(3)每一個判定的所有可能的輸出結(jié)果至少產(chǎn)生1次,。

    Chilenski原則^[9]：對于一個具有n個條件的判定,，滿足MC/DC準(zhǔn)則的測試用例至少有n＋1組。

    MC/DC對^[10]：一個MC/DC對是一對真值向量,，該向量中一個條件值變化時可使得判定有不同的結(jié)果,。

    矩陣組合邏輯運(yùn)算規(guī)則：將矩陣的條件部分進(jìn)行兩兩組合，同時將結(jié)果部分按邏輯運(yùn)算符進(jìn)行邏輯運(yùn)算,，如式(1)所示：

    語法二叉樹：將一個判定從左到右依次轉(zhuǎn)化為對應(yīng)的語法二叉樹,，其中條件P_i采用葉子節(jié)點(diǎn)表示，and,、or等邏輯運(yùn)算符采用非葉子節(jié)點(diǎn)表示,。以(P₁ and P₂)and(P₃ or P₄)為例，其對應(yīng)的語法二叉樹如圖1所示,。

    語法二叉樹遞歸規(guī)則：從葉子節(jié)點(diǎn)開始往根節(jié)點(diǎn)逐層遞歸,。左、右子樹為葉子節(jié)點(diǎn)時,，按“語法二叉樹與矩陣對應(yīng)關(guān)系”獲得對應(yīng)矩陣,。若某一子樹的左子樹或右子樹為非葉子節(jié)點(diǎn)時，利用該子樹的左,、右矩陣,，按“矩陣組合邏輯運(yùn)算規(guī)則”進(jìn)行運(yùn)算：若為and運(yùn)算，先將左矩陣中每一行與右矩陣中結(jié)果為1的行進(jìn)行運(yùn)算,，然后將右矩陣中每一行與左矩陣中結(jié)果為1的行進(jìn)行運(yùn)算,，最后合并運(yùn)算結(jié)果；如為or運(yùn)算時,，選取相應(yīng)矩陣中結(jié)果為0的行進(jìn)行運(yùn)算,。運(yùn)算結(jié)果即為該子樹對應(yīng)的判定的最小測試用例集。遞歸到根節(jié)點(diǎn)時,，即獲得整個判定的最小測試用例集,。

    命題  按語法二叉樹遞歸規(guī)則可得到MC/DC最小測試用例集。

    證明  以n表示語法二叉樹的高度,，當(dāng)n=2時，左,、右子樹為葉子節(jié)點(diǎn),，可直接獲得判定的矩陣,，即最小測試用例集，結(jié)論成立,。當(dāng)n>2時,，由于該子樹的左、右矩陣符合Chilenski原則,，因此左,、右矩陣的行集合其實(shí)就是MC/DC對集合。左,、右矩陣按“矩陣組合邏輯運(yùn)算規(guī)則”運(yùn)算時,，以and運(yùn)算為例（or運(yùn)算同理），左矩陣中MC/DC對分別與右矩陣中結(jié)果為1的行進(jìn)行運(yùn)算(此處只證明合理性,，因此右矩陣中有多個結(jié)果為1的行時,，只選取其中一行運(yùn)算即可。實(shí)際操作時,，結(jié)果為1的行均進(jìn)行運(yùn)算,，這樣可獲得完備的最小測試用例集)，實(shí)際上只是在該MC/DC對中增加了右矩陣中的同一組條件,，MC/DC對數(shù)量不變,。同樣原理，將右矩陣中MC/DC對與左矩陣中結(jié)果為1的行進(jìn)行運(yùn)算后,，該MC/DC對中增加了左矩陣中的同一組條件,，MC/DC對數(shù)量不變。然后合并運(yùn)算結(jié)果,，此時針對左,、右子樹中條件的MC/DC對構(gòu)造完畢，即該子樹的最小測試用例集構(gòu)造完畢,。遞歸至根節(jié)點(diǎn)時,，就可獲得針對全部條件的MC/DC對，即該語法二叉樹的MC/DC最小測試用例集,，證畢,。

2 算法設(shè)計與驗證

2.1 算法步驟

    按照上述規(guī)則及定義，MC/CD最小測試用例集的生成算法步驟如下：

    (1)將判定轉(zhuǎn)換為語法二叉樹,；

    (2)從葉子節(jié)點(diǎn)開始,，按“語法二叉樹遞歸規(guī)則”向根節(jié)點(diǎn)逐層遞歸，遞歸過程按“語法二叉樹與矩陣對應(yīng)關(guān)系”采用矩陣表示子樹,，并按“矩陣組合邏輯運(yùn)算規(guī)則”進(jìn)行運(yùn)算獲得子樹對應(yīng)的矩陣,；

    (3)遞歸至語法二叉樹的根節(jié)點(diǎn)時，算法結(jié)束。

2.2 算法驗證

2.2.1 零耦合條件的判定的驗證

2.2.2 帶耦合條件的判定的驗證

    帶耦合條件的判定是指判定中存在部分重復(fù)條件,。以(P₁ and P₂ and P₃) or (P₁ and (P₂ and P₄))為例,，條件P₁、P₂重復(fù)出現(xiàn)(判定中重復(fù)出現(xiàn)的條件采用P₁′,、P₂′表示),。按照算法步驟先轉(zhuǎn)化為語法二叉樹，如圖2所示,。

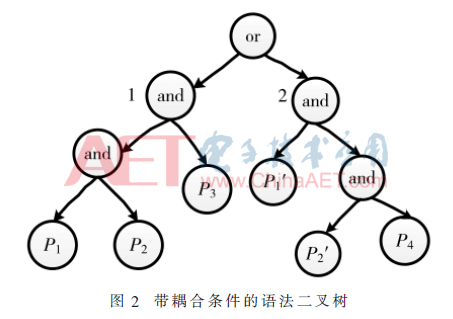
    在處理帶耦合條件的判定時,，在2.1算法步驟中增加兩個規(guī)則：(1)一致性規(guī)則。在遞歸過程中遇到重復(fù)條件時,，為保證重復(fù)條件取值的一致性,，在矩陣中選擇重復(fù)條件取值一致的MC/DC對進(jìn)行運(yùn)算。(2)構(gòu)造規(guī)則,。為了保證一致性,，矩陣中MC/DC對數(shù)量受到了限制，不能滿足Chilenski原則,，因此需要通過構(gòu)造方式來滿足該原則,。以左矩陣中與重復(fù)條件相關(guān)的MC/DC對為基礎(chǔ)，補(bǔ)充構(gòu)造右矩陣中條件,，構(gòu)造時需遍歷相應(yīng)子樹進(jìn)行正確性驗證,。構(gòu)造完右矩陣中條件對應(yīng)的MC/DC對后，在其基礎(chǔ)上反轉(zhuǎn)非重復(fù)條件,，構(gòu)造左矩陣中的MC/DC對,。

3 實(shí)驗分析

    最小真值表法、快速生成算法等算法都是依據(jù)判定中的多種條件不斷進(jìn)行判斷,、歸約,，從而依次生成每個用例。本算法從語法二叉樹的葉子端向根節(jié)點(diǎn)遞歸,，每次遞歸得到的都是當(dāng)前子樹的MC/DC最小測試用例集,，其測試用例集始終限制在最小維度，而且遞歸過程只需進(jìn)行簡單的矩陣組合邏輯運(yùn)算,，因此,，在手動生成測試用例方面更快速、簡潔,、直觀,。最小真值表法、快速生成算法等算法只能獲得唯一一個最小測試用例集,，無法得到其余的最小測試用例集,。保證冗余的測試用例是有必要的^[12],。在2.2.1的驗證中，本算法同時生成了兩個最小測試用例集,，可以證明該判定有且僅有這兩個最小測試用例集,，這表明本算法生成了完備的最小測試用例集，其可在不影響測試組大小范圍的情況下有效提高錯誤檢測效率,。同時，在進(jìn)行矩陣組合邏輯運(yùn)算時,，任意選取左或右矩陣中結(jié)果為1(and運(yùn)算符)或0(or運(yùn)算符)的一行進(jìn)行運(yùn)算,，即可獲得唯一的最小真值矩陣。

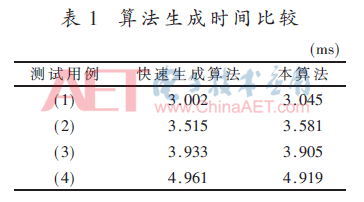
    在判定(零耦合條件)的唯一最小測試用例的自動生成所需時間方面,，本算法首先生成語法二叉樹,，然后由葉子節(jié)點(diǎn)向根節(jié)點(diǎn)進(jìn)行遞歸，由于左,、右子樹可以實(shí)現(xiàn)并發(fā)遞歸,，因此對于左、右子樹較對稱的,、葉子節(jié)點(diǎn)較多的語法二叉樹而言,，其所需的時間優(yōu)于快速生成算法，具有快速生成測試用例的優(yōu)勢,。算法生成時間比較結(jié)果見表1,，其中非布爾表達(dá)式分別為：(1)(P₁ or P₂) and (P₃ and P₄)；(2)(P₁ and P₂ and P₃) or (P₄ and P₅),；(3)(P₁ and P₂ and P₃) or (P₄ and (P₅ and P₆)),；(4)(P₁ and P₂ and (P₃ or P₄)) or (P₅ and (P₆ and P₇ or P₈))。但是,，本算法需要存儲空間存儲矩陣,，其對存儲空間的要求高于快速生成算法。

    最小真值表法,、快速生成算法等算法只適合處理由標(biāo)準(zhǔn)運(yùn)算符and,、or構(gòu)成的零耦合條件的判定，規(guī)避了對帶耦合條件的判定的分析,。本算法適用于存在耦合條件的判定的分析,，其在生成測試用例過程中雖需要遍歷語法二叉樹進(jìn)行驗證，但生成的測試用例集滿足MC/DC要求,，且遍歷時只需對部分子樹進(jìn)行遍歷,，因此數(shù)量遠(yuǎn)小于全遍歷情況，對帶耦合條件的判定的分析具有一定借鑒意義,。與謝祥南等^[7]的耦合條件的MC/DC測試用例集生成算法相比,，本算法比較簡潔直觀,，但對于復(fù)雜的強(qiáng)耦合條件的判定的分析，本算法還有不足,，需要進(jìn)一步深入研究,。

4 結(jié)論

    不同測試工具對于代碼的覆蓋能力是有區(qū)別的，通常能夠支持MC/DC的測試工具的價格極其昂貴^[13],。本文提出的算法基于語法二叉樹,，從葉子節(jié)點(diǎn)開始采用符合MC/DC覆蓋準(zhǔn)則的矩陣進(jìn)行遞歸，可快速,、直觀,、有效地處理零耦合條件的判定，并生成完備的的最小測試用例集,，適合自動或手動生成,。對于帶耦合條件的復(fù)雜判定，本算法也有一定適用性,，其生成的測試用例集合遠(yuǎn)遠(yuǎn)低于全遍歷情況,，這在減輕測試工程師工作量、提高工作效率方面有一定借鑒意義,。下一步將對帶耦合條件的判定做進(jìn)一步研究,，提高其算法的生成效率。

參考文獻(xiàn)

[1] 朱少民.全程軟件測試(3版)[M].北京：人民郵電出版社,，2019：130-132.

[2] 王吉茂,，尹平.軟件測試用例執(zhí)行優(yōu)化研究[J].計算機(jī)工程與設(shè)計，2013,，12(1)：4242-4246.

[3] 王瑞,，田宇立，周東紅,，等.面向故障定位的基于MC/DC的測試用例約簡方法[J].計算機(jī)科學(xué),，2015，42(10)：170-174.

[4] DONG L,，LINGHUAN H,，RUIZHI G.Improving MC/DC and fault detection strength using combinatorial testing[C].2017 IEEE International Conference on Software Quality，Reliability and Security Companion(QRS-C).Prague,，Czech Republic：IEEE,，2017：84-88.

[5] 朱曉波，楊偉民,，葉芯.更改條件/判定覆蓋最小真值表生成算法及其應(yīng)用[J].上海理工大學(xué)學(xué)報,，2007，29(1)：84-88.

[6] 段飛雷,，吳曉,，張凡,，等.MC/DC最小測試用例集快速生成算法[J].計算機(jī)工程，2009,，35(17)：40-45.

[7] 謝祥南,，魏延棟.耦合條件的MC/DC測試用例集生成算法[J].計算機(jī)系統(tǒng)應(yīng)用，2017,，26(6)：164-169.

[8] 黃孝倫.基于圖的MC/DC最小測試用例集快速生成算法[J].計算機(jī)系統(tǒng)應(yīng)用,，2012，21(11)：145-147.

[9] SEKOU K,，ALEXIS T,，MIHAELA B.Practical methods for automatic MC/DC test case generation of Boolean expressions[C].2015 IEEE Autotestcon.National Harbor，MD,，USA：IEEE，2015.

[10] 周睿.基于Java編譯器的MC/DC測試覆蓋方法設(shè)計[J].軟件導(dǎo)刊,，2016,，15(8)：39-41.

[11] 袁軍.基于MC/DC最小測試用例集設(shè)計方法研究[J].航空電子技術(shù)，2010,，41(3)：51-54.

[12] VILKOMIR S,，BAPTISTA J，DAS G.Using MC/DC as a black-box testing technique[C].2017 IEEE 28th Annual Software Technology Conference(STC).Gaithersburg,，MD,，USA：IEEE，2017：25-28.

[13] 楊憶文.一種自動化測試系統(tǒng)中為I/O建模及約束提取的方法[M].北京：北京郵電大學(xué),，2014.

作者信息:

黃孝倫,，王  東

(重慶市衛(wèi)生信息中心，重慶401120)