文獻(xiàn)標(biāo)識碼: A
DOI:10.16157/j.issn.0258-7998.190981
中文引用格式: 俞美鑫,施衛(wèi),蔣龍,等. 基于GA-BP神經(jīng)網(wǎng)絡(luò)的動力鋰電池SOC估算[J].電子技術(shù)應(yīng)用,2020,46(1):104-107,112.
英文引用格式: Yu Meixin,Shi Wei,Jiang Long,et al. SOC estimation of power lithium battery based on GA-BP neural network[J]. Application of Electronic Technique,2020,46(1):104-107,112.
0 引言
隨著能源危機(jī)和環(huán)境問題的日益嚴(yán)重,近些年來世界各國紛紛加大力度發(fā)展新能源汽車,以減少對環(huán)境污染和對化石燃料的依賴。鋰離子電池作為電動汽車主流的儲能元件,其性能直接影響整車性能的表現(xiàn)[1]。而動力電池為電動汽車系統(tǒng)的關(guān)鍵部件,以磷酸鐵鋰為正極材料的鋰電池因其高能量密度及耐高溫性能等優(yōu)點得到了廣泛的運用。電池荷電狀態(tài)(SOC)是顯示電池運行狀態(tài)的重要參數(shù),決定了電動汽車的可續(xù)駛公里數(shù),國內(nèi)外目前已經(jīng)取得了海量的研究成果,如安時計量法、開路電壓法放電試驗法[2]等。這些方法的實現(xiàn)需要電池長時間靜置或要求電流變化幅度不大的情況下方能得到精準(zhǔn)數(shù)據(jù)。
動力鋰電池內(nèi)部復(fù)雜的電化學(xué)反應(yīng)和運行狀況中不斷變化的各類因素之間的非線性關(guān)系致使傳統(tǒng)SOC值估算方法存在較大誤差。而BP神經(jīng)網(wǎng)絡(luò)算法是一種模擬人腦學(xué)習(xí)技能的新型算法,無需建立準(zhǔn)確的數(shù)學(xué)模型,通過分析輸入量和輸出量之間的對應(yīng)關(guān)系,為輸出量建立模型。因BP神經(jīng)網(wǎng)絡(luò)是基于誤差逆向傳播的多層前饋網(wǎng)絡(luò)特性[3],該算法收斂速度較慢且易陷入局部極小化。而遺傳算法(GA)則是一種通過模擬自然界的選擇與生物進(jìn)化機(jī)理來尋找最優(yōu)解智能算法,具有較強(qiáng)的收斂性和魯棒性,它與神經(jīng)網(wǎng)絡(luò)相結(jié)合恰好可以完美解決易陷入局部最優(yōu)點的問題,并能明顯加快網(wǎng)絡(luò)收斂速度。
1 GA-BP神經(jīng)網(wǎng)絡(luò)
1.1 GA算法
遺傳算法(Genetic Algorithm,GA)是模擬生物在自然環(huán)境中的遺傳和進(jìn)化的過程而形成的自適應(yīng)全局優(yōu)化搜索算法[4]。遺傳搜索算法可同時處理群體中的多個體以達(dá)到快速優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值,從而使優(yōu)化后的BP神經(jīng)網(wǎng)絡(luò)能夠更好地預(yù)測函數(shù)輸出。遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的要素包括群種初始化、適應(yīng)度函數(shù)、選擇操作、交叉操作和變異操作[5]。
1.1.1 種群初始化
個體編碼方式為實數(shù)編碼,每個實數(shù)作為一個染色體的一個基因位,可免去編碼解碼步驟,便于遺傳操作簡化。實數(shù)串分為四部分,分別為由輸入層至隱含層權(quán)值W1、隱含層至輸出層權(quán)值W2、隱含層閾值B1、輸出層閾值B2。
1.1.2 適應(yīng)度函數(shù)
由個體得到BP神經(jīng)網(wǎng)絡(luò)初始權(quán)值和閾值,再用訓(xùn)練數(shù)據(jù)進(jìn)行BP神經(jīng)網(wǎng)絡(luò)訓(xùn)練后預(yù)測系統(tǒng)輸出,將期望輸出與預(yù)測值之間的誤差絕對值記作個體適應(yīng)度F,如式(1)所示:

其中n為網(wǎng)絡(luò)輸出節(jié)點個數(shù),yi為i點期望輸出值,oi為i點預(yù)測輸出值,k為系數(shù)。
1.1.3 選擇操作
此方案選擇的輪盤賭法是在適應(yīng)度比例的選擇策略下完成的,單個個體被選擇的概率pi如下:

式中,神經(jīng)網(wǎng)絡(luò)第i個節(jié)點的適應(yīng)度值為Fi,種群個體數(shù)目設(shè)定為N。
1.1.4 交叉操作
因個體使用實數(shù)編碼,故選擇實數(shù)交叉法,第L個染色體al和第K個染色體kl在j位的交叉操作情況如:

1.1.5 變異操作
隨機(jī)抽取個體i的第j個基因變異,變異結(jié)果如式(5)所示:

式中,amin為基因aij的下限值,amax為基因aij的上限值,0≤r≤1。
1.2 BP神經(jīng)網(wǎng)絡(luò)
BP(Back Propagation)神經(jīng)網(wǎng)絡(luò)是由輸入層、輸出層和隱含層構(gòu)成的,具有“信號向前傳遞、誤差反向傳播”的網(wǎng)絡(luò)模型特征[6],是一種前饋型多層感知器。在信號向前傳遞中,輸入信號從輸出層經(jīng)隱含層逐次處理,直至輸出層每一次神經(jīng)元狀態(tài)會影響下一層神經(jīng)元狀態(tài),如若輸出層得出數(shù)值與期望值不同,則轉(zhuǎn)入反向傳播階段,再根據(jù)預(yù)測誤差調(diào)整網(wǎng)絡(luò)的閾值和權(quán)值,從而使BP神經(jīng)網(wǎng)絡(luò)輸出層不斷向期望值逼近[7]。汽車動力鋰電池的SOC值與放電電流、電池電壓、電池正極溫度均存在非線性關(guān)系。BP神經(jīng)網(wǎng)絡(luò)首先使用經(jīng)遺傳算法優(yōu)化后的輸入輸出參數(shù)對其進(jìn)行訓(xùn)練,再通過訓(xùn)練好的GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測系統(tǒng)的輸出值,判斷誤差范圍是否在合理區(qū)間內(nèi),最終確定該算法在動力電池SOC值預(yù)測上的可行性。
2 動力鋰電池SOC估算模型建立
建立GA-BP算法的動力電池SOC估算模型必須分別確定BP神經(jīng)網(wǎng)絡(luò)和遺傳算法中的各設(shè)計參數(shù)。
2.1 BP神經(jīng)網(wǎng)絡(luò)設(shè)計與GA-BP運算參數(shù)確定
在建立BP神經(jīng)網(wǎng)絡(luò)前,首先建立網(wǎng)絡(luò)結(jié)構(gòu)框架。根據(jù)理論研究表明,在兩組非線性相關(guān)的輸入和輸出數(shù)據(jù)中,若其他各條件選擇合理,一般三層BP神經(jīng)網(wǎng)絡(luò)就能滿足設(shè)計的精度要求,同時輸入與輸出參數(shù)的選擇直接影響神經(jīng)網(wǎng)絡(luò)輸入層與輸出層節(jié)點數(shù)目和變換函數(shù)類型,選擇合理的輸入?yún)?shù)能夠獲得良好的網(wǎng)絡(luò)性能,同時可以提高網(wǎng)絡(luò)的訓(xùn)練速度和精度等,輸入?yún)?shù)的選擇一般遵循的基本原則是選擇對網(wǎng)路輸出影響大、容易測量且輸入變量之間無相關(guān)性或相關(guān)性較小的參數(shù)。在汽車動力鋰電池SOC神經(jīng)網(wǎng)絡(luò)輸出參數(shù)選擇中,電池端電壓、電池放電電流和電池正極溫度都可以通過單片機(jī)采集,CAN數(shù)據(jù)傳輸收集到,且三者與鋰電池SOC值聯(lián)系緊密,故將動力電池的電壓、溫度、電流作為神經(jīng)網(wǎng)絡(luò)三個輸入變量,鋰電池的SOC值作為BP神經(jīng)網(wǎng)絡(luò)的唯一輸出端變量。從而訓(xùn)練樣本可以表達(dá)為[V I T SOC]的向量形式,V為電池端電壓、I為電池充放電電流、T為電池正極溫度、SOC為剩余電量[8],如圖1所示。
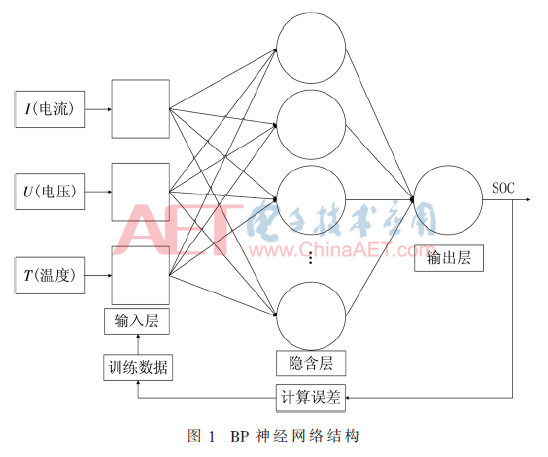
BP神經(jīng)網(wǎng)絡(luò)的節(jié)點數(shù)可根據(jù)一般經(jīng)驗確定,通過試驗得到一個較合理的結(jié)果。常用經(jīng)驗公式為:

其中,m為輸出節(jié)點數(shù);n為輸入節(jié)點數(shù);P為隱藏層節(jié)點數(shù);a為1~10之間的整數(shù),結(jié)合網(wǎng)絡(luò)預(yù)測精度,在這里取a=4,故隱藏層節(jié)點個數(shù)為6。
遺傳算法種群規(guī)模設(shè)定為50,遺傳疊代次數(shù)為100次,變異概率為0.09,交叉概率為0.4。
2.2 GA-BP神經(jīng)網(wǎng)絡(luò)構(gòu)建
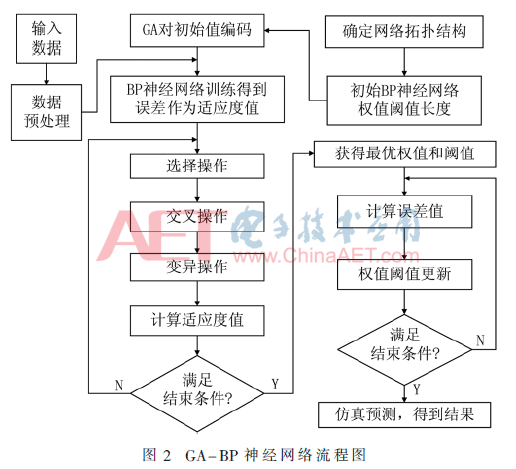
GA-BP神經(jīng)網(wǎng)絡(luò)框架構(gòu)建的核心思想就是將遺傳算法的啟發(fā)式尋優(yōu)和全局優(yōu)化特征運用于神經(jīng)網(wǎng)絡(luò)閾值和權(quán)值的訓(xùn)練,再通過BP算法的誤差逆?zhèn)鞑ヌ卣鬟M(jìn)一步反饋優(yōu)化,最終達(dá)到智能尋優(yōu)目的[9]。基本結(jié)構(gòu)框圖如圖2所示。
3 數(shù)據(jù)采集及試驗結(jié)果分析
本文選取的汽車動力電池為磷酸鐵鋰電池,試驗平臺為江蘇理工學(xué)院與中德諾浩公司合作開發(fā)的電池管理試驗臺架,如圖3所示。

電池放電試驗參數(shù)經(jīng)飛思卡爾MC9S12中央處理器運算后通過CAN通信協(xié)議傳輸信號,經(jīng)MCGS組態(tài)軟件實現(xiàn)電池電壓數(shù)據(jù)采集實時更新,如圖4所示。

電池額定電壓為3.2 V,額定容量為60 Ah,內(nèi)阻≤2 mΩ,過充保護(hù)電壓3.65±0.05 V,放電截止電壓為2.5±0.05 V,放電工作溫度為-20 ℃~60 ℃,充電工作溫度為
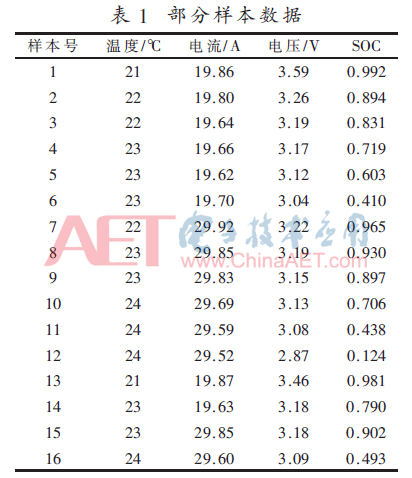
-10 ℃~55 ℃[10]。在額定溫度(20±5 ℃)情況下,先用1/3C(20 A)恒流充電,電池電壓到達(dá)3.65 V時靜置2小時,放電過程分別采用1/3C、1/2C的放電電流進(jìn)行放電試驗,到達(dá)設(shè)定時間后停止放電,在放電時段分別隨機(jī)采集電池的放電電流、電壓、溫度、剩余電量值,歸一化處理制作成樣本數(shù)據(jù),如表1所示。
選取1至12號組樣本作為訓(xùn)練樣本數(shù)據(jù),13至16組用作測試樣本數(shù)據(jù),運用MATLAB工具箱搭建網(wǎng)絡(luò)模型,通過樣本學(xué)習(xí)得到最優(yōu)化的閾值和權(quán)值,帶入兩組測試樣本中測試該算法的可行性[11]。設(shè)置已使用遺傳算法優(yōu)化后的BP神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)速率為0.01,均方差為0.000 001,迭代次數(shù)為5 000次。將隨機(jī)初始BP神經(jīng)網(wǎng)絡(luò)與經(jīng)遺傳算法優(yōu)化過的權(quán)值和閾值兩種情況下的訓(xùn)練誤差曲線做對比[12],如圖5、圖6所示。

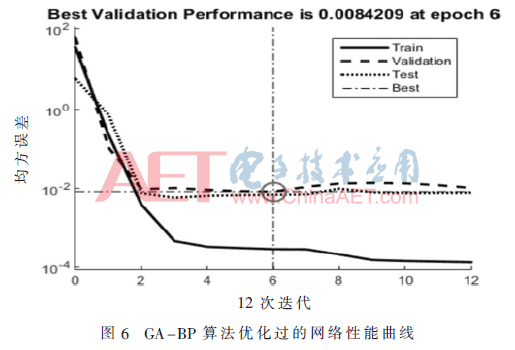
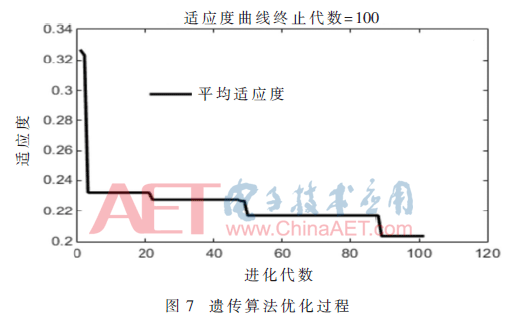
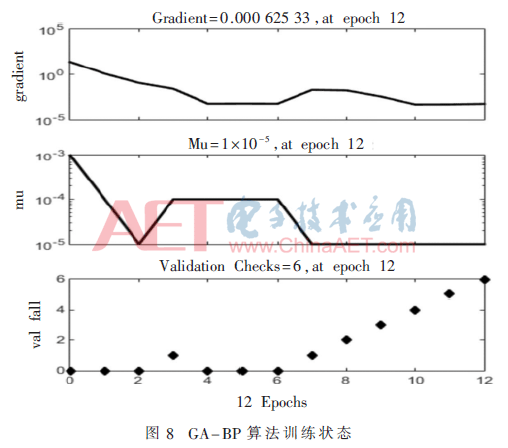
明顯看出經(jīng)GA-BP算法優(yōu)化過的網(wǎng)絡(luò)當(dāng)訓(xùn)練次數(shù)接近6次時,誤差很小且已達(dá)到目標(biāo)要求精度。遺傳算法優(yōu)化過程中適應(yīng)度變化過程和GA-BP算法的訓(xùn)練狀態(tài)圖如圖7、圖8所示。
隨機(jī)抽取測試樣本中的兩組電池試驗數(shù)據(jù),將電池SOC的實際值分別經(jīng)BP神經(jīng)網(wǎng)絡(luò)和GA-BP神經(jīng)網(wǎng)絡(luò)算法仿真后的數(shù)據(jù)進(jìn)行對比,如表2所示。

由表2可知,經(jīng)過遺傳算法訓(xùn)練后的BP網(wǎng)絡(luò)相比誤差逆?zhèn)鞑ニ惴▽崿F(xiàn)了對電池SOC精準(zhǔn)估算,克服了傳統(tǒng)算法應(yīng)過度依賴建立數(shù)學(xué)模型的弊端,為實現(xiàn)動力電池SOC的精確估算提供了一種新途徑。
4 結(jié)論
本文選用運用于純電動汽車的60 Ah的磷酸鐵鋰鋰電池為研究對象,針對影響電池SOC值的復(fù)雜非線性關(guān)系影響因素,提出了將遺傳算法和BP神經(jīng)網(wǎng)絡(luò)算法相結(jié)合,提升收斂速度和迭代過程的平穩(wěn)性,從而達(dá)到迅速獲取權(quán)值和閾值的目的,并在所得試驗數(shù)據(jù)的基礎(chǔ)上進(jìn)行仿真試驗,驗證了GA-BP神經(jīng)網(wǎng)絡(luò)算法在動力鋰電池SOC估算中具有良好的全局搜索能力、高度的魯棒性優(yōu)勢和準(zhǔn)確性。
參考文獻(xiàn)
[1] 孫濤,龔國慶,陳勇.鋰電池參數(shù)辨識模型的設(shè)計與研究[J].電子技術(shù)應(yīng)用,2019,45(3):127-130.
[2] 李世光,汪洋,王建志,等.基于改進(jìn)EKF算法的鋰電池SOC預(yù)估研究[J] .電子技術(shù)應(yīng)用,2017,43(9):87-89,97.
[3] 劉冰,郭海霞.MATLAB神經(jīng)網(wǎng)絡(luò)超級學(xué)習(xí)手冊[M].北京:人民郵電出版社,2014.
[4] 包子陽,余繼周,楊杉.智能優(yōu)化算法及其MATLAB[M].北京:電子工業(yè)出版社,2018.
[5] MATLAB中文論壇.MATLAB神經(jīng)網(wǎng)絡(luò)30個案例分[M].北京:北京航空航天大學(xué)出版社,2010.
[6] 呂聰穎.智能優(yōu)化方法的研究及應(yīng)用[M].北京:中國水利水電出版社,2014.
[7] 趙剛,孫豪賽,羅淑貞.基于BP神經(jīng)網(wǎng)絡(luò)的動力電池SOC估算[J].電源技術(shù)研究與設(shè)計,2016(4):818-819.
[8] 周美蘭,趙強(qiáng),周永勤.改進(jìn)的PSO-BP神經(jīng)網(wǎng)絡(luò)估算磷酸鐵鋰電池SOC[J].哈爾濱理工大學(xué)學(xué)報,2015(4):892.
[9] 黃妙華,嚴(yán)永剛,朱立明.改進(jìn)BP神經(jīng)網(wǎng)絡(luò)的磷酸鐵鋰電池SOC估算[J].武漢理工大學(xué)學(xué)報,2014(12):790-793.
[10] 高文敬.動力電池SOC估算方法研究與BMS開發(fā)[D].淄博:山東理工大學(xué),2018.
[11] 程澤華.基于人工神經(jīng)網(wǎng)絡(luò)的MATLAB接觸線磨耗預(yù)測型研究[D].北京:中國鐵道科學(xué)研究院,2018.
[12] 譚霞.基于GA優(yōu)化的MIV-BP神經(jīng)網(wǎng)絡(luò)連續(xù)血壓無創(chuàng)監(jiān)測方法研究[D].重慶:重慶大學(xué),2018.
作者信息:
俞美鑫,施 衛(wèi),蔣 龍,王 浩
(江蘇理工學(xué)院 機(jī)械工程學(xué)院,江蘇 常州213000)

