0 引言

    2012年10月,，Keccak^[1]算法被美國NIST選為SHA3^[2](Secure Hash Algorithm 3)的標準算法,。Keccak算法具有加密速度快、散列值位分布均勻,、抗碰撞性強等特點,，并且較其他雜湊算法具有更好的硬件實現(xiàn)性能，因此Keccak算法得到了廣泛關注,。

    目前關于Keccak算法硬件實現(xiàn)的研究中,，對填充過程的設計和完整算法電路的分析較少，如文獻[3]對算法結構的分析只基于了置換過程而沒有考慮填充過程,；并且這類研究聚焦于算法的實現(xiàn)性能而沒有考慮面積資源,，如文獻[4]采用流水線實現(xiàn)置換過程，文獻[5],、[6]將寄存器插入置換過程間減少關鍵路徑,，文獻[7]串聯(lián)多級置換運算單元，這些提高性能方式都是以面積資源的增加為代價,。

    本文通過分析Keccak完整算法流程,，以32 bit作為輸入數(shù)據(jù)位寬，對算法數(shù)據(jù)填充和狀態(tài)置換過程設計獨立的模塊,，簡化了控制結構的復雜度,，實現(xiàn)了加密過程中的數(shù)據(jù)填充與置換過程的并行執(zhí)行；通過分析和實驗結果可知,，本文設計的結構平衡了性能和資源消耗,，并具有較高的能效。

1 Keccak算法過程描述

    Keccak算法是基于海綿結構設計的雜湊算法,，海綿結構具有可變長度輸入和任意長度輸出,。

1.1 海綿結構

    海綿結構使用置換f建立具有可變輸入長度和任意輸出長度的函數(shù)[f,，pad，r],，置換f對固定數(shù)量的比特進行操作,，其位寬為b。

    如圖1所示,，海綿結構的置換過程分為吸收階段和擠壓階段,。

    吸收階段：輸入信息M根據(jù)規(guī)則pad進行填充后得到信息P，然后將P按照r bit長度劃分成消息分組M₀,，M₁,，…，M_n-1,。M₀與置換的初始狀態(tài)(初始狀態(tài)為全0)的前r bit進行異或,，后c bit保持不變，將得到的b(b=r+c)比特狀態(tài)信息輸入到置換函數(shù)f,；在吸收階段后續(xù)的每個置換函數(shù)f的輸入都是當前消息分組M_i與上個置換函數(shù)f的輸出前r bit異或得到的結果,。當最后一個消息分組M_n-1進入置換函數(shù)產(chǎn)生結果后，吸收階段結束,。

    擠壓階段：根據(jù)使用者所需要的輸出信息Z,，從b bit狀態(tài)信息的前r bit進行截取,；當所需輸出長度|Z|>r,，首先將當前狀態(tài)信息的前r bit截取，然后將當前狀態(tài)數(shù)據(jù)輸入到置換函數(shù)f,，從函數(shù)結果截取r bit,，直到達到使用者所需的輸出長度后，擠壓階段結束,。

1.2 填充規(guī)則

    Keccak算法的填充規(guī)則記為pad,，具體過程如下：

    在輸入消息M后添加單個比特1,，然后添加n比特0,，最后添加單個比特1，使得填充后的長度|P|為r的整數(shù)倍,。其中,，n為滿足|M|+2+n≡0 mod r的最小整數(shù)；填充比特長度最短為2,，最長為r+1,。

    基于海綿結構的Keccak算法理論上可以生成任意長度的散列值，但NIST為了配合SHA2散列值,，在SHA3標準中規(guī)定了4種模式,。不同的模式下只有消息分組r與輸出長度Z的位寬不同,，具體數(shù)據(jù)如表1所示。

1.3 置換過程

    Keccak算法的置換過程記為Keccak-f[b],，是針對狀態(tài)數(shù)組A的迭代過程,，迭代輪數(shù)n_r=24。狀態(tài)數(shù)組A是一個三維數(shù)組,，數(shù)組中的元素屬于GF[2]域,，狀態(tài)數(shù)組也可以看出一個位寬為1 600 bit的比特串S，狀態(tài)數(shù)組的置換函數(shù)f包括θ,、ρ,、π、χ,、ι 5個步驟,。其詳細描述如下：

1.3.1 映射規(guī)則

    比特串S到狀態(tài)數(shù)組A的映射規(guī)則為A[x][y][z]=S[64×(5×y+x)+z]，其中(0≤x≤5,，0≤y<5,，0≤Z<64)。示例如下：

1.3.2 步驟描述

    (1)步驟θ：

2 Keccak算法ASIC設計

    分析海綿體結構和Keccak算法流程可知,，Keccak寄存填充過程與置換過程是能夠并行執(zhí)行的,，其具體過程如圖2所示。

    從圖2中看出,，前一組消息分組進行置換時可以同時進行第二個消息分組的寄存或填充,，因此在Keccak硬件電路中設計填充模塊和置換模塊來并行執(zhí)行填充寄存過程和置換過程。

    Keccak硬件完整電路結構如圖3所示,，填充模塊用于外部數(shù)據(jù)的接收,，消息分組的寄存和算法的填充過程；置換模塊負責狀態(tài)數(shù)組的吸收擠壓過程和數(shù)據(jù)輸出過程,。

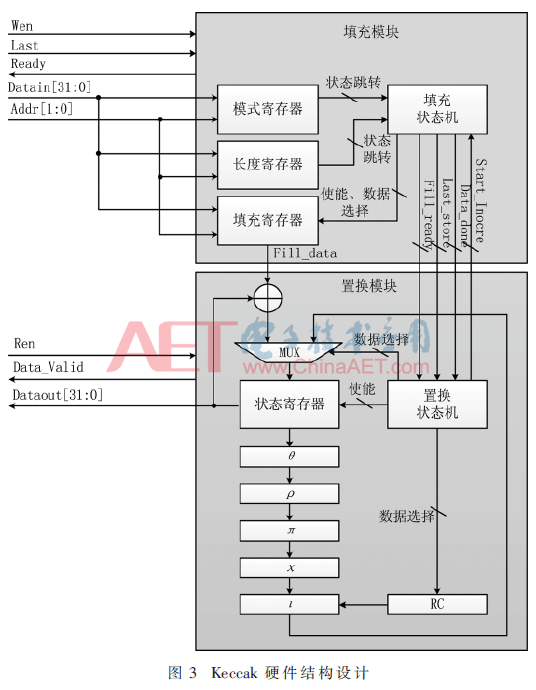
2.1 填充模塊

    在外部信號作用下,，填充模塊每個時鐘周期接收串行輸入的32 bit消息數(shù)據(jù)，當寄存的消息數(shù)據(jù)構成一個r bit的消息分組后,，將寄存的消息分組送入空閑狀態(tài)的置換模塊,；若外部信號顯示當前為最后一個消息分組，則需要先對該消息分組進行填充,，此過程由填充狀態(tài)機進行控制,。

    填充模塊的內(nèi)部包括存儲當前SHA3標準的模式寄存器，存儲最后消息分組有效長度位信息的長度寄存器,， 存儲消息分組的填充寄存器,，以及控制數(shù)據(jù)輸入或填充過程的狀態(tài)機。

    填充模塊的輸入信號包括寫信號Wen,、地址信號Addr,、最后一個消息分組的標志信號Last,、位寬為32 bit輸入數(shù)據(jù)Datain及來自填充模塊的運算啟動標識信號start_Incore。

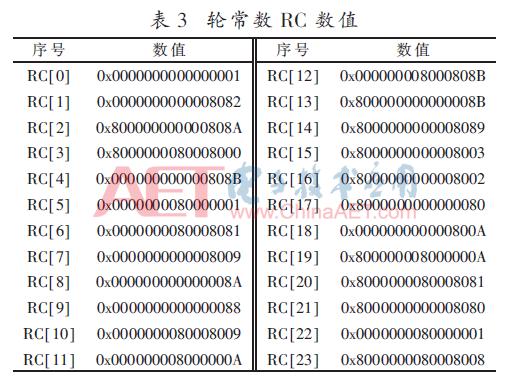
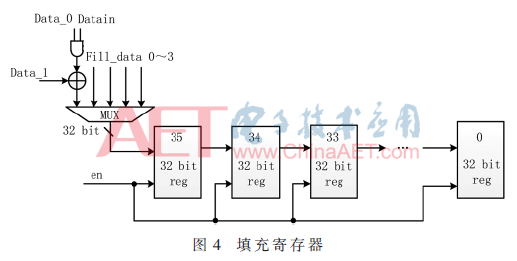
    填充寄存器電路結構如圖4所示,，填充寄存器由36個32 bit移位寄存器構成,，用于存儲外部輸入的消息分組和內(nèi)部產(chǎn)生的填充數(shù)據(jù)。當外部32 bit數(shù)據(jù)Datain進入寄存器后,，填充模塊內(nèi)部的計數(shù)器進行計數(shù)操作,，當計數(shù)值達到當前的SHA3模式所對應的消息分組時，代表一個消息分組存儲完成,。若該過程中Last信號出現(xiàn),，由填充狀態(tài)機控制進行填充操作。通過對填充過程進行分析,，得到可能出現(xiàn)的4種填充數(shù)據(jù)Fill_data,，其數(shù)值如表4所示。

    填充狀態(tài)機的跳轉是由模塊內(nèi)的計數(shù)器,、模式寄存器存儲數(shù)據(jù),、長度寄存器存儲數(shù)據(jù)控制，狀態(tài)機的轉換圖如圖5所示,。

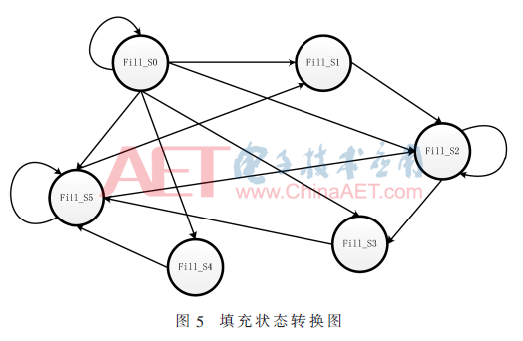
    圖5中的各個狀態(tài)所代表的含義及功能如表5所示：Fill_S0代表狀態(tài)機空閑,，該狀態(tài)下填充模塊由外部控制接收消息分組數(shù)據(jù)、長度數(shù)據(jù),、模式數(shù)據(jù),；Fill_S1、Fill_S2,、Fill_S3,、Fill_S4是進行數(shù)據(jù)填充的狀態(tài)；Fill_S5是數(shù)據(jù)準備狀態(tài),，在該狀態(tài)下代表當前的消息分組全部進入填充寄存器,，等待送入置換模塊。

2.2 置換模塊

    Keccak的置換模塊主要執(zhí)行狀態(tài)數(shù)組的存儲,、置換以及數(shù)據(jù)輸出三個操作,。

    在置換模塊中，設計了一組狀態(tài)寄存器,，用于存儲25×32 bit狀態(tài)數(shù)組,，將置換函數(shù)映射成為θ,、ρ,、π、χ,、ι 5個運算單元,。置換模塊內(nèi)部的狀態(tài)機具有4個狀態(tài),，其狀態(tài)轉換圖分別如圖6所示。

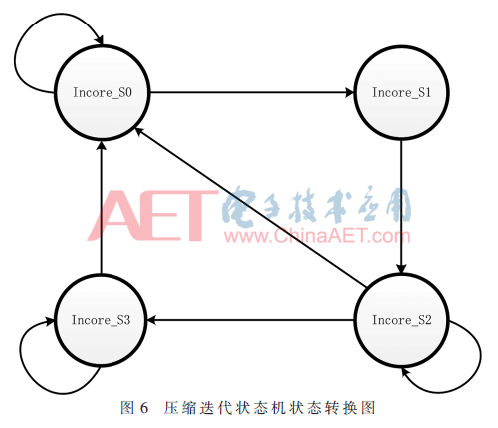
    圖6中的各個狀態(tài)所代表的含義及功能如表6所示：Incore_S0為空閑態(tài),，該狀態(tài)下模塊內(nèi)部不執(zhí)行任何操作,；Inocre_S1狀態(tài)下狀態(tài)寄存器組中的數(shù)據(jù)與填充模塊存儲完畢的消息分組異或來完成狀態(tài)的更新；Incore_S2狀態(tài)下,，狀態(tài)數(shù)組進行24輪迭代置換操作,；當所有消息分組完成置換過程后，進入Incore_S3狀態(tài)等待數(shù)據(jù)輸出,。

3 Keccak硬件結構能效分析

    Keccak算法電路的填充置換兩個過程結構的面積開銷占比如表7所示,。

    表7中的數(shù)據(jù)占比沒有包含電路中的控制部分；填充過程的非組合邏輯面積開銷主要為填充寄存器,，置換過程的非組合邏輯面積開銷主要為狀態(tài)寄存器,。

    目前Keccak算法實現(xiàn)區(qū)別主要在于置換結構，圖7為三種主要實現(xiàn)方式,。

    圖7中基礎結構是本文所使用的結構,，特點是資源占用率少；展開結構是將置換函數(shù)兩級級聯(lián),，通過時鐘周期的減少來提高吞吐率,；流水線結構是通過提高整個算法結構頻率，并采用流水線來執(zhí)行不同信息來提高吞吐率,。以基礎置換結構的Keccak完整電路面積,、頻率、吞吐率,、能效為單位,，其他兩結構各數(shù)值如表8所示。

    表8中將本文Keccak算法電路的面積,、頻率,、吞吐率、能效作為標準,，比較了兩級的展開結構和流水線結構,；由于輸入位寬為32 bit，導致填充寄存過程時鐘周期多于置換過程,，因此展開結構中置換過程時鐘周期的減少實際并沒有影響單個消息分組處理時鐘周期,，所以該結構吞吐率反而降低。流水線結構中增加的狀態(tài)寄存器必須放置在各步驟之間,，因此頻率并不能隨插入寄存器的數(shù)量提升,；當消息分組寄存填充所占時鐘周期大于置換過程迭代輪數(shù)，n級流水線結構中需要n個填充寄存結構，才能滿足數(shù)據(jù)填充過程進行流水,，因此流水線結構面積開銷大,。

    綜合上述分析，對于實現(xiàn)完整Keccak算法實現(xiàn),，置換過程的展開結構和流水線結構較基礎結構能效反而降低,。

4 KeccaK算法ASIC實現(xiàn)及性能評估

    本文提出的結構和其他文獻結構實現(xiàn)結果對比如表9和表10所示。

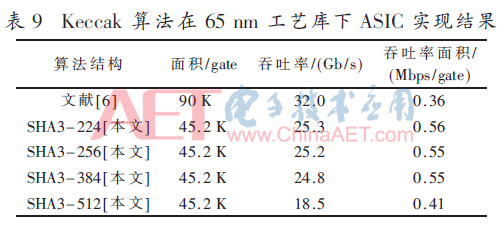
    文獻[6]所設計的Keccak算法硬件電路采用64 bit輸入位寬,，置換過程采用三輪級聯(lián)展開,。分析表8的數(shù)據(jù)中可知，將置換過程級聯(lián)展開會消耗大量的面積資源,，雖然提高了吞吐率,，但導致了整個硬件電路能效的降低。從上表中數(shù)據(jù)分析得知,，本文結構較文獻[6]結構在能效上提高了約50%,。

    文獻[5]采用了兩級流水線結構，以面積資源換取了吞吐率的提高,，但是當外界數(shù)據(jù)以單任務方式出現(xiàn)時,，該結構吞吐率會降低一倍。從表中數(shù)據(jù)分析得到,，當外界數(shù)據(jù)按多任務出現(xiàn)時,，本文結構與文獻[5]的流水線結構能效相同；當外界數(shù)據(jù)按單任務出現(xiàn)時,，本文結構較文獻[5]的流水線結構提高了約95%,。

    從實驗結果及對比分析中可以看出，置換過程采用基本結構實現(xiàn)的完整Keccak算法硬件電路具有較高能效,。本文采用模塊化思想所設計的Keccak算法硬件電路具有資源面積開銷小,、能效高的特點。

參考文獻

[1] BERTONI G,，DAEMEN J,，PEETERS M，et al.Keccak[C].EUROCRYPT,，2013：313-314.

[2] DWORKIN M J.SHA-3 standard：permutation-based hash and extendable-output functions[S].Federal Information Processing Standard(NIST-FIPS)-202,，2015.

[3] IOANNOU L，MICHAIL H E,，VOYIATZIS A G.High performance pipelined FPGA implementation of the SHA-3 hash algorithm[C].2015 4th Mediterranean Conference on Embedded Computing(MECO).IEEE,，2015.

[4] SHARMA J，KOPPAD D.Low power and pipelined secure hashing algorithm-3(SHA-3)[C].India Conference.IEEE,，2017.

[5] MESTIRI H,，KAHRI F,，BEDOUI M,et al.High throughput pipelined hardware implementation of the KECCAK hash function[C].International Symposium on Signal.IEEE，2017.

[6] Wu Xufan,，Li Shuoguo.High throughput design and implementation of SHA-3 hash algorithm[C].2017 International Conference on Electron Devices and Solid-State Circuits(EDSSC).IEEE，2017.

[7] WONG M M,，HAJ-YAHYA J.A new high throughput and area efficient SHA-3 implementation[C].2018 IEEE International Symposium on Circuits and System,，2018.

作者信息:

庹  釗，陳  韜,，李  偉,，南龍梅

(解放軍戰(zhàn)略支援部隊信息工程大學 密碼工程學院，河南 鄭州450001)