a男人天堂,PR社44-三寸萝莉收费下载

基于滑動窗的積分多普勒偽距平滑算法研究

2018年電子技術(shù)應(yīng)用第12期

殷彪,，耿生群,，趙昀

北京航空航天大學(xué) 電子信息工程學(xué)院，北京100191

摘要： 在載體處于高速運動的條件下，導(dǎo)航信號可能隨時被遮擋,、衰落,、干擾,，同時載波多普勒的快速變化,，導(dǎo)致利用載波相位平滑偽距來提高定位精度的方法不再適用。此外,，在以載波多普勒積分值代替載波相位平滑偽距的傳統(tǒng)方法中,，由于采用固定窗計算平滑偽距初值，極易將奇異值或者誤差較大的偽距觀測量包含到初值中,，而且隨著時間增長,，載波多普勒的累積誤差會越來越大。為解決上述問題,，研究了基于滑動窗處理偽距初值的積分多普勒偽距平滑算法,。該算法通過滑動精估窗實時計算偽距初值，以此為基礎(chǔ),，利用平滑窗內(nèi)的多普勒加權(quán)累積和計算出偽距變化量,，實現(xiàn)偽距觀測量平滑。在充分考慮了電離層,、累積誤差等因素的基礎(chǔ)上設(shè)計了精估窗和平滑窗的長度,。靜態(tài)定位實驗和高動態(tài)模擬飛行試驗結(jié)果均表明，該算法可以有效提高接收機的導(dǎo)航定位精度,，同時解決了傳統(tǒng)方法中異常值影響平滑初值和載波多普勒誤差累積問題,。

關(guān)鍵詞： 高動態(tài) 滑動窗平滑初值積分多普勒偽距平滑

中圖分類號： TN961
文獻標(biāo)識碼： A
DOI：10.16157/j.issn.0258-7998.181161
中文引用格式： 殷彪，耿生群,，趙昀. 基于滑動窗的積分多普勒偽距平滑算法研究[J].電子技術(shù)應(yīng)用,，2018,，44(12)：81-84.
英文引用格式： Yin Biao，Geng Shengqun,，Zhao Yun. Research on algorithm based on sliding-window integral Doppler smoothing pseudorange[J]. Application of Electronic Technique,，2018，44(12)：81-84.

Research on algorithm based on sliding-window integral Doppler smoothing pseudorange

Yin Biao,，Geng Shengqun,，Zhao Yun

School of Electronics and Information Engineering，University of Aeronautics and Astronautics,，Beijing 100191,，China

Abstract： The navigation signals can be blocked, faded and interfered, when a satellite navigation receiver is carried by high dynamic vehicles and working in complex environments. Besides, the carrier Doppler measurements in the navigation receiver will rapidly change due to high dynamics. As a result, the algorithms of smoothing the pseudorange measurements with the carrier-phase measurements are no longer applicable. Furthermore, the conventional techniques of smoothing the pseudo-range measurements with the integral of carrier Doppler measurements, generally use a fixed window for calculating the initial value of pseudoranges, and then can cause a large error in the initial value if the measurements with significant biases or the outliers are involved in the fixed window. In addition, the error in the integral of carrier Doppler measurements is accumulated over the smoothing time. Therefore, an improved algorithm of smoothing the pseudo-range measurements with the integral of carrier Doppler measurements is proposed. By employing a sliding window to replace the fixed window for calculating the initial value of pseudoranges, more accurate initial values for smoothing can be estimated. And the changes in pseudorange are calculated based on the weighted accumulation of carrier Doppler measurements. In consideration of the ionospheric variations, accumulated error and other factors, the lengths of the sliding window and the consequent smoothing window are chosen. The experimental results in both the static positioning and the simulated flight navigation show that the positioning accuracy is improved. Moreover, the estimation error in the initial value of pseudoranges and the accumulated error in the integral of carrier Doppler measurements are efficiently reduced.

Key words : high dynamic；sliding-window,；smoothing initial value,；integral Doppler；smoothing pseudorange

0 引言

20世紀(jì)80年代開始,，HATCH R首次提出采用載波相位平滑偽距的方法來提高定位精度^[1]，此種方法可以在靜態(tài)或低動態(tài)應(yīng)用中有效改善接收機的測距結(jié)果^[2],。但是在高動態(tài)條件下,，會遇到周跳問題，且解決難度較大,。

針對載波相位平滑偽距出現(xiàn)周跳的問題,，國內(nèi)其他學(xué)者研究了固定窗積分多普勒平滑偽距算法^[3]，固定窗即平滑初值只采取固定的點數(shù)計算一次,。這種算法利用了多普勒頻移觀測值獨立于載波相位觀測值,，不因載波相位發(fā)生周跳而產(chǎn)生變化^[4-6]的原理，有效避免了處理周跳問題,，同時提高了定位精度,。

對于固定窗積分多普勒平滑偽距這種算法，在平滑過程中需要利用多普勒加權(quán)累積和代替多普勒積分,，所產(chǎn)生的累積誤差會向平滑后的偽距引入偏差^[7],。而且在高動態(tài)條件下，接收機所處環(huán)境復(fù)雜多變,。這種條件下采用固定窗計算平滑初值會將奇異值包含到初值中且無法剔除,，最終將造成巨大的定位偏差。

針對上述問題,，本文提出了一種基于滑動窗計算初值的積分多普勒偽距平滑算法,，有效解決了固定窗積分多普勒平滑偽距出現(xiàn)的問題。

1 積分多普勒偽距平滑原理分析

由于多徑噪聲和接收機熱噪聲項對載波跟蹤環(huán)引起的相噪值在厘米級,，只有偽碼相噪值的1%^[8],，載波相位觀測量精度高于偽碼觀測量兩個數(shù)量級。為了提高偽距觀測量的精度，同時利用積分多普勒在數(shù)值上表現(xiàn)為載波相位變化但是不受載波周跳影響的這一性質(zhì)^[9],，本節(jié)研究了積分多普勒偽距平滑算法,，具體如下。

已知0時刻衛(wèi)星s₁的偽距為ρ(0),，那么k時刻衛(wèi)星s₁的偽距ρ(k)為：

其中,，f_doppler為多普勒頻率。

2 滑動窗積分多普勒偽距平滑算法

本文上一節(jié)推導(dǎo)了任一時刻偽距ρ(k)基于積分多普勒的表達式,。本節(jié)將基于此式推導(dǎo)基于滑動窗的積分多普勒偽距平滑公式,。

首先，計算平滑初值,。對于任一時刻i,，利用接下來較長一段時間的碼相位觀測量和積分多普勒值對當(dāng)前時刻的偽距進行精估計^[10]。假設(shè)用于精估計的歷元個數(shù)為N,，即計算初始值的精估窗長度為N,，則對i時刻的偽距精估計結(jié)果可以表示為：

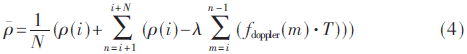
式中，T為歷元間隔時間,，ρ(i)為i時刻碼相位觀測偽距,。由于接收機無法提供連續(xù)時間域上的載波多普勒信息，在式中采用加權(quán)和的形式代替式(4)中的積分,。

其次,，算法利用i時刻精估計得出的偽距對后續(xù)偽距進行平滑處理，假設(shè)需處理的歷元為i時刻后的第M個歷元,，設(shè)此時刻為k,，則該歷元時刻的偽距平滑結(jié)果可表示為：

隨后將平滑偽距和碼相位偽距進行加窗組合形成高精度偽距：

最后，當(dāng)前觀測量提取完畢后,，精估窗口向后滑動一個歷元,，窗長度不變，計算第i+1時刻的初值,，用新的精估計初值計算第M+i+1時刻的平滑偽距,。此后時刻重復(fù)上述步驟。

本算法每次獲取新的偽距值都重新計算平滑初值,，從而有效解決了加權(quán)和累積誤差問題和初值包含奇異值的問題,。算法具體執(zhí)行流程如圖1所示。

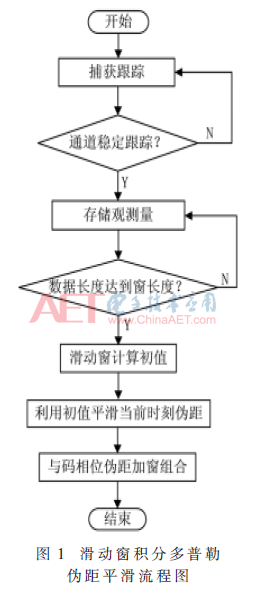
3 實驗與分析

3.1 滑動窗異常值和累積誤差處理實驗

累積誤差實驗：采用本文的滑動窗算法與傳統(tǒng)的固定窗算法分別對單點進行長時間定位,，其中傳統(tǒng)的固定窗初值窗長為100個歷元,，本文的滑動窗精估計窗長也為100個歷元，對定位結(jié)果誤差進行對比分析,，具體如圖2和圖3所示,。

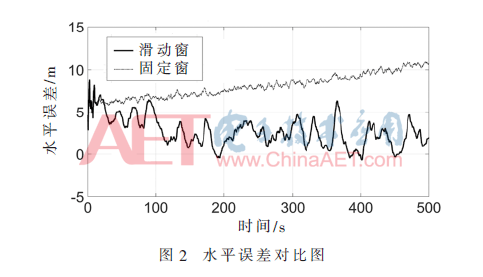
從圖中可以看出,，隨著時間變長，傳統(tǒng)的固定窗算法定位誤差在累積增大,，在測量時間段內(nèi)最大累積誤差達到了8 m,，而滑動窗定位結(jié)果誤差依然處于正常水平，穩(wěn)定后水平誤差在6 m以內(nèi),，高度誤差在10 m以內(nèi),。

奇異值處理實驗：衛(wèi)星號為6的衛(wèi)星在第20 s的偽距上加誤差3 000 m，采用本文的滑動窗算法與傳統(tǒng)的固定窗算法分別對單點進行長時間定位,，具體如圖4和圖5所示,。

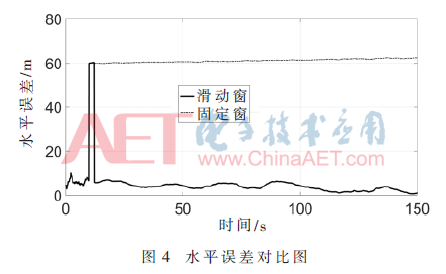
從圖中可以看出，當(dāng)偽距出現(xiàn)跳變時,，傳統(tǒng)固定窗算法定位出現(xiàn)巨大偏差,，而滑動窗算法會隨著窗的滑動使定位誤差逐漸回歸正常。在高動態(tài)場景中,，由于環(huán)境復(fù)雜,，偽距觀測量極易發(fā)生跳變，本文提出的滑動窗算法將極大地發(fā)揮作用,。

3.2 靜態(tài)實驗

靜態(tài)實驗實驗時間為2018年1月15日,，地點參考坐標(biāo)為東經(jīng)116.322 795 4°，北緯39.958 994°,，高度為71 m，觀測時間為180 s,，數(shù)據(jù)輸出頻率為10 Hz,。分別對偽距平滑前后定位結(jié)果和測速結(jié)果進行對比分析，圖6~圖8為平滑前后的接收機定位測速誤差,。

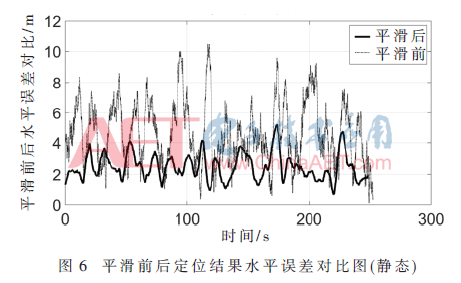
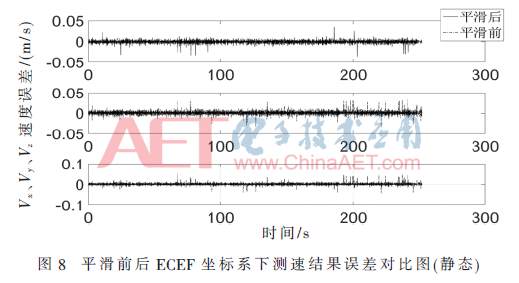
從靜態(tài)定位結(jié)果誤差對比圖中可以看出,，滑動窗算法有效地提高了定位精度。

3.3 動態(tài)實驗

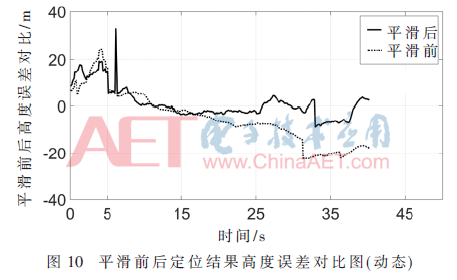
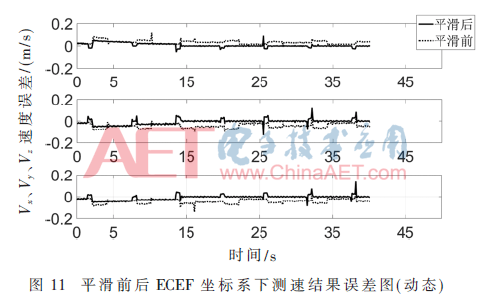
動態(tài)實驗采用GPS衛(wèi)星信號模擬器產(chǎn)生炮彈飛行軌跡,，使用高動態(tài)GPS導(dǎo)航接收機實時跟蹤定位,。炮彈發(fā)射初速度為80 m/s，最大過載40 g,，初始點海拔高度為1 351 m,，射程為10 km，發(fā)射仰角45°,，方向角北偏東30°,。采用接收機平滑前后的定位測速結(jié)果與模擬器原始彈道軌跡做對比，分別計算其誤差,。

動態(tài)定位結(jié)果誤差對比圖如圖9~圖11所示,，從中可以看出,，本文提出的滑動窗積分多普勒偽距平滑算法在高動態(tài)場景下同樣可以有效提升定位精度。

3.4 實驗分析

本文分別以滑動窗異常值和累積誤差處理實驗,、靜態(tài)實驗和動態(tài)實驗對本文提出的基于滑動窗的積分多普勒偽距平滑算法進行了分析驗證,。

其中靜態(tài)實驗定位誤差均值如表1所示，動態(tài)實驗定位誤差均值如表2所示,。

需要說明的是,，本算法在定位過程的前期接收機處于偽距平滑的初始化階段，其測速誤差及定位誤差明顯大于偽距平滑完成后的對應(yīng)結(jié)果,。

從表中可以看出,，無論是動態(tài)場景還是靜態(tài)場景，滑動窗積分多普勒偽距平滑算法均優(yōu)于傳統(tǒng)的固定窗算法,。

4 結(jié)論

本文研究了基于滑動窗的積分多普勒偽距平滑算法,，著重解決了固定窗多普勒偽距平滑算法的缺點：用多普勒加權(quán)和代替多普勒積分消除了累積誤差，解決了復(fù)雜環(huán)境下平滑初值包含奇異值的問題,。進行了累積誤差,、異常值處理和靜態(tài)定位實驗，實驗結(jié)果驗證了本文算法優(yōu)于傳統(tǒng)的固定窗算法,。并且利用導(dǎo)航衛(wèi)星信號模擬器,，對本算法進行了模擬彈道軌跡的跟蹤定位實驗，結(jié)果表明,，此算法在高動態(tài)條件下有效地提升了定位精度,，其中水平精度平均提升7 m，高度平均提升3.79 m,，在ECEF坐標(biāo)系下x,、y、z 3個方向速度精度平均提升0.01 m/s,、0.03 m/s,、0.03 m/s。

參考文獻

[1] HATCH R.The synergism of GPS code and carrier measurements[C].Proceedings of the Third International Geodetic Symposium on Satellite Doppler Positioning,，Las Cruces,，New Mexico，U.S.A.,，1982,，1：1213-1232.

[2] 周澤波，沈云中,，李博峰.基于相位平滑偽距與多普勒數(shù)據(jù)的GPS動態(tài)定位[J].大地測量與地球動力學(xué),，2008，28（3）：59-63.

[3] 隋葉葉,，楊小江,，柳濤.載波相位平滑偽距算法研究與精度分析[J].電子工程設(shè)計,，2013，21(8)：112-115.

[4] 常志巧,，郝金明,，李俊義.利用多普勒觀測檢測周跳和粗差[J].測繪通報，2008（3）：28-30.

[5] 王甫紅,，張小紅,，黃勁松.GPS單點測速的誤差分析及精度評價[J].武漢大學(xué)學(xué)報(信息科學(xué)版)，2007,，32（6）：515-519.

[6] 李立言.高動態(tài)GNS信號處理及解算關(guān)鍵技術(shù)研究[D].杭州：浙江大學(xué),，2012.

[7] 謝鋼.GPS原理與接收機設(shè)計[M].北京：電子工業(yè)出版社，2011.

[8] JAY A.Fattel,，Aided Navigation,，GPS with high rate sensors[M]. McGraw Hill，2008.

[9] 金磊,，陳帥,，劉亞玲，等.基于積分多普勒平滑偽距的導(dǎo)航算法研究[J].航天控制,，2015,，33(1)：61-65.

[10] 孫偉，段順利.GPS多普勒偽距平滑定位與測速方法[J].測繪科學(xué),，2016,，41(12)：81-84.

作者信息:

殷彪，耿生群,，趙昀

（北京航空航天大學(xué) 電子信息工程學(xué)院,，北京100191)