0 引言

    電力系統(tǒng)中非線性負荷的大量增加，特別是電力電子裝置的廣泛應用,，使電網(wǎng)中產(chǎn)生大量的諧波與間諧波,，從而嚴重影響了電能質量，對電力系統(tǒng)的安全與經(jīng)濟運行造成極大的影響^[1],。因此,，準確測量電網(wǎng)中的諧波信號，實時掌握電網(wǎng)中的諧波參量,，對防止諧波危害,，維護電網(wǎng)的安全運行是十分必要的^[2]。

    目前電力系統(tǒng)諧波分析的主要方法有模擬濾波器法^[3]、小波變換法^[4],、神經(jīng)網(wǎng)絡法和快速傅里葉算法(FFT)^[5],。相較于前幾種方法，快速傅里葉算法(FFT)易于在ARM,、DSP等嵌入式系統(tǒng)中實現(xiàn),，計算速度快、效率高,、技術成熟^[5],，因此FFT諧波檢測法應用最多。

    在同步采樣下,，對諧波信號運用FFT算法檢測,，能準確得到諧波信號參數(shù)。而對電網(wǎng)中的動態(tài)信號即使采用頻率跟蹤技術,，也很難做到嚴格地同步采樣,。在非同步采樣下運用FFT對信號進行參數(shù)檢測時，非同步采樣與數(shù)據(jù)截斷所引起的頻譜泄漏和柵欄效應造成的誤差較大,。針對諧波檢測中FFT檢測法的柵欄效應和頻譜泄漏問題,，加窗插值是消除柵欄和抑制頻譜泄漏的有效方法。經(jīng)典窗有Hanning窗^[6],、Blckman-Harris窗^[7]等余弦窗。Hanning窗的特點是插值公式較簡單,，而且計算量小,，但是分析精度較低；Blckman-Harris窗插值FFT算法的特點是分析精度較高,，但是插值公式過于復雜,，且計算量大，因而使用不便,。本文在分析 Rife-Vincent 窗頻譜特性的基礎上,，提出了基于三次樣條函數(shù)的加Rife-vincent自卷積窗插值FFT算法。卷積窗在幅值和頻率檢測方面有較高的諧波檢測精度,。通過Rife-vincent自卷積窗對采樣信號進行加權截斷,，可有效抑制頻譜泄漏，減少諧波間的相互干擾,，進一步提高信號參數(shù)檢測的準確度,，并且通過三次樣條函數(shù)，有效地消除了柵欄效應,。通過MATLAB軟件,，對含諧波的信號進行檢驗仿真，驗證了本文所提的算法能夠對諧波信號進行精確分析。

1 基于三次樣條函數(shù)的加Rife-vincent自卷積窗插值FFT算法

    Rife-Vincent自卷積窗具有優(yōu)良的旁瓣性能,，采用Rife-Vincent自卷積窗能夠有效抑制頻譜泄漏,，減少諧波間的相互干擾，通過使用三次樣條函數(shù)對Rife-Vincent自卷積窗加權截斷后的信號進行分析,，能夠準確得到各諧波信號的參數(shù),。

    以頻率為f_h、幅值為A_h,、初相位為φ_h,、最高諧波次數(shù)為h的諧波信號x(t)為例：

    此嵌套形式的三次樣條插值算法的形成過程如下：

    (1)δ在區(qū)間[0，1]等步長取11個插值點(α_i,，δ_i),，(α_i+1，δ_i+1)…,；

    (2)取三次樣條插值函數(shù)的邊界條件為自然邊界條件,；

    (3)調用MATLAB中的spline函數(shù)分段擬合出10段三次樣條插值函數(shù)（分段越多擬合精度越高）；

    (4)通過以上3步求得三次樣條函數(shù),；

    (5)離線求出式(8)所示嵌套形式的三次樣條插值函數(shù),。

2 仿真分析

    為驗證本文所提算法的有效性與準確性，選用弱諧波信號進行仿真,，仿真模型如下：

    其中基波信號頻率f₀=50 Hz,，采樣頻率f_s=1 500 Hz，窗函數(shù)長度N=2 048,，各次諧波信號的幅值與相位如表1所示,，其中相位為本文給出的初值。仿真結果如表2,、表3所示,。

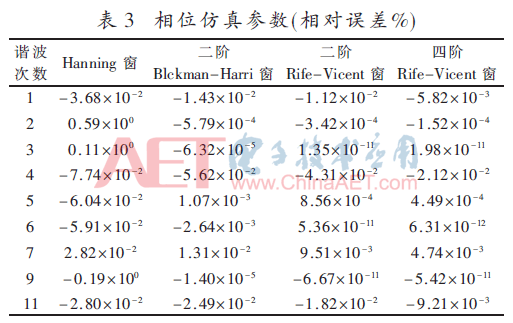
    從表2、3中可以看出：

    (1)與直接FFT運算相比,，加窗插值FFT算法大大提高了諧波檢測精度,；

    (2)隨著窗函數(shù)的旁瓣衰減速度的加快、旁瓣峰值的降低,，抑制頻泄露能力得到提高,，信號檢測精度提高；

    (3)較經(jīng)典窗相比,，卷積窗在幅值和頻率檢測方面進一步提高了諧波檢測精度,；

    (4)由于p階Rife-Vincent自卷積窗優(yōu)越的旁瓣性能，二階Rife-Vincent自卷積窗的諧波檢測精度較二階Nutall自卷積窗檢測精度有所提高,，以五次諧波和八次諧波為例,，二階Rife-Vincent自卷積窗的諧波檢測精度較二階Nutall自卷積窗在幅值方面相對誤差最大可降低0.1%,，相位檢測相對誤差最大可降低0.1%；

    (5)隨著Rife-Vincent自卷積窗卷積階數(shù)p的增加,，檢測精度也有所提高,，相對誤差大約降低了0.1%，特別是四階Rife-Vincent自卷積窗在三次,、六次和九次諧波,，檢測結果非常接近真實值。

3 結論

    采用FFT算法對電力系統(tǒng)諧波分析時,，由于頻譜泄漏的影響,，使得諧波參數(shù)的檢測有較大的誤差。為減小頻譜泄漏的影響,，本文選用旁瓣性能優(yōu)越,、時域結構簡單的四項一階Rife-vincent窗作為母窗，構造p階Rife-Vincent自卷積窗,。與經(jīng)典窗,、經(jīng)典自卷積窗相比，本文所選用的p階Rife-Vincent自卷積窗旁瓣峰值低,、旁瓣衰減速度快,，能夠有效抑制頻譜泄漏，減少諧波間的相互干擾,，提高諧波檢測精度,。采用三次樣條函數(shù)逼近幅值比公式，避免解高次方程,，簡化了計算,，有效地消除了柵欄效應。通過仿真結果可以看出,，本文所提的基于三次樣條函數(shù)的加p階Rife-Vincent自卷積窗插值FFT算法，在弱諧波信號檢測中,，能夠有效提高檢測精度,，準確檢測諧波參數(shù)。

參考文獻

[1] 劉冬梅,，鄭鵬,，何怡剛，等.幾種諧波檢測加窗插值FFT算法的比較[J].電測與儀表,，2013,，50(12)：51-55.

[2] 牛勝鎖，梁志瑞,，張建華,，等.基于四項余弦窗三譜線插值FFT的諧波檢測方法[J].儀器儀表學報,，2012，33(9)：2002-2008.

[3] 牛勝鎖,，梁志瑞,，張建華，等.基于三譜線插值FFT的電力系統(tǒng)諧波分析[J].中國電機工程學報,，2012,，32(16)：130-136.

[4] 張鵬，李紅斌.一種基于離散小波變換的諧波分析方法[J].電工技術學報,，2012,，27(3)：252-258.

[5] 溫和，滕召勝,，郭斯羽,，等.Hanning自卷積窗函數(shù)及其諧波分析應用[J].中國科學E輯：技術科學，2009,，39(6)：1190-1198.

[6] 高索丹,，巴鵬.Hanning窗在電力系統(tǒng)諧波分析中的應用[J].自動化技術與儀表，2008,，27(11)：124-127.

[7] 趙文春,，馬偉明，胡安.電機測試中諧波分析的高精度fft算法[J].中國電機工程學報,，2001,，21(12)：83-87.

[8] KINCAID D，CHENEY W.數(shù)值分析[M].王國榮,，俞耀明,，徐兆亮，譯.北京：機械工業(yè)出版社,，2005.

[9] 孫同明,，許珉，楊育霞.應用三次樣條函數(shù)快速計算插值FFT算法[J].電力自動化設備,，2007,，27(6)：60-62.

作者信息：

張瑩瑩

(河南省信陽市質量技術監(jiān)督檢驗測試中心，河南 信陽464000)