0 引言

    在靜電放電(Electrostatic Discharge,，ESD)抗擾度試驗中，ESD模擬器易受機械振動,、環(huán)境變化以及設備自身產生的輻射場等干擾,，這些干擾最終會耦合到測量電纜中形成高頻振蕩噪聲^[1-2]。雖然實驗中采用了標準IEC61000-4-2規(guī)定的法拉第籠等屏蔽措施^[3],，但仍存在無法消除的噪聲干擾,。

    針對實測ESD電流波形存在干擾噪聲的問題,，本文將小波分析與自適應卡爾曼(Kalman)濾波算法結合用于ESD電流波形的去噪分析。根據人體-金屬模型(Human Body-Metal Model,，HMM)的放電電流構建了染噪的ESD電流信號模型,，小波去噪方法在該模型上進行去噪性能分析，以確定適于ESD電流波形去噪的小波函數和分解層次,。實際應用中,，ESD電流波形在小波閾值去噪的基礎上，引入自適應Kalman濾波算法做優(yōu)化處理,，從而更有效地實現(xiàn)降噪,。

1 ESD電流波形去噪方法

    ESD電流波形去噪方法的主要思想是利用小波分析方法對ESD電流信號進行多層分解，有效提取噪聲信息,，對包含噪聲信息的高頻小波系數使用限閾值法處理,，小波重構獲得相對穩(wěn)定的ESD電流觀測數據。再根據ESD電流觀測數據的信息,，使用自適應Kalman濾波算法做優(yōu)化處理^[4],。

1.1 小波閾值去噪方法

    小波去噪方法種類很多，本文采用的是實現(xiàn)簡單且計算量較小的閾值去噪方法^[5],，該方法步驟如下：

    (1)一維信號的小波變換：選擇合適的小波函數和分解層次,，對ESD電流信號進行離散小波變換。

    (2)小波系數限閾值處理：噪聲信息主要集中在高頻小波系數中,，對各層高頻小波系數做限閾值處理,。

    (3)一維信號的小波重構：由小波變換后的尺度系數和閾值法處理后的小波系數重構出去噪信號。

    通常使用的閾值處理方法分為以下兩種^[6]：

    常用的閾值獲取方法有啟發(fā)式閾值,、極大極小原則閾值、固定閾值和Stein無偏估計原則閾值4種,。文獻[6]中將小波閾值去噪方法用于ESD電流波形的去噪分析,，結果表明：使用Stein無偏估計原則閾值對ESD電流波形的去噪效果較好。

1.2 自適應Kalman濾波

    SAGE A P和HUSA G W提出的自適應濾波算法具有原理簡單,、實時性好的特點^[7],。利用Sage-Husa的極大后驗估值器對未知噪聲進行統(tǒng)計估計，將其遞推形式與Kalman濾波算法相結合可以構成噪聲統(tǒng)計值不斷修正的自適應Kalman濾波算法,。簡化的Sage-Husa自適應Kalman濾波算法描述如下：

2 加噪ESD電流信號模型建立

    為了確定小波閾值去噪方法的效果,，可以使用ESD電路模型構建放電回路，利用數值解法計算出符合標準規(guī)范的ESD電流數據,，通過疊加隨機高斯白噪聲,，模擬實際環(huán)境中的靜電放電電流信號。

2.1 考慮寄生參量的HMM-ESD電流數值計算

    標準IEC61000-4-2中給出的ESD事件源于人體靜電起電的模擬,，可以使用人體ESD電路模型來構建ESD發(fā)生器的放電電路^[8],。這里采用了考慮寄生參量的HMM-ESD電路^[9],，構建的接觸式放電回路，如圖1所示,。

    根據HMM-ESD回路特性,，可以獲得能夠描述該電路模型回路特性的一階微分方程組：

其中，u_B(t),、u_P(t),、u_HA(t)分別對應電容C_B、C_P,、C_HA的電壓,；i_B(t)、i_HA(t)分別對應電感L_B,、L_HA的電流,。儲能元件初始狀態(tài)已知，則可以使用常微分方程的數值解法對其進行求解,。

    常微分方程的數值解法通常有歐拉(Euler)方法,、龍格-庫塔(Runge-Kutta)方法^[10-11]和阿當姆斯(Adams)方法等。本文使用的是計算量小且精度較高的Adams預測校正方法,，考慮Adams預測校正算法是四步法,，需要借助單步的Runge-Kutta算法預測最初4個節(jié)點的值^[12]。針對HMM-ESD回路特性方程組的四階Runge-Kutta算法描述如下：

    將Runge-Kutta方法計算出的最初4個節(jié)點y_m(0),、y_m(1),、y_m(2)、y_m(3)的值作為初始參數傳遞給Adams預測校正算法,。再由4步的顯式Adams公式做預測,，3步的隱式Adams公式作校正，依次遞推計算后續(xù)節(jié)點的值,。

    回路元件參數設定：C_B=141 pF,，R_B=330 Ω，L_B=0.12 μH,，C_P=1.5 pF,，C_HA=8 pF，R_HA=40 Ω,，L_HA=2.5 μH,。儲能元件初始狀態(tài)：u_B(0)=6 000 V，u_P(0)=u_HA(0)=0 V,，i_B(0)=i_HA(0)=0 A,。取步長h=0.025 ns，數值計算獲得HMM-ESD電流波形，如圖2所示,。該波形不僅符合標準參數規(guī)范,，而且還能很好地反映實測過程中的寄生振蕩現(xiàn)象，40 GHz采樣頻率的6 kV實測ESD電流波形如圖3所示,。

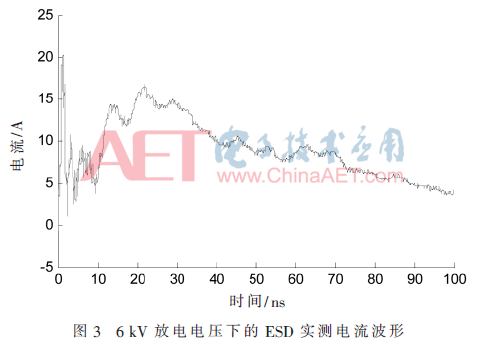
2.2 HMM-ESD電流信號疊加噪聲

    含噪ESD電流信號的模型表示如下：

式中,，s(n)采用基于Adams預測校正方法計算的HMM-ESD電流數值解的4 096個采樣點作為無噪信號；e(n)采用信噪比為19 dB的高斯白噪聲信號,；y(n)為無噪原始信號與噪聲信號的合成信號,，其電流波形如圖4所示。

    小波去噪方法在此模型上進行,，使用信噪比（Signal Noise Ratio,，SNR）和均方誤差（Mean Squared Error，MSE）作為評估去噪方法有效性的指標：

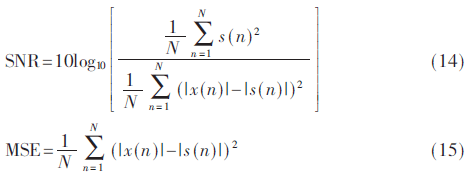
其中,，x(n)是去噪處理后的數據,。去噪效果評價準則是信噪比SNR越大，均方誤差MSE越小,，去噪效果就越好,。

3 小波去噪實驗數據分析

    加噪ESD電流波形的小波去噪分析中，分別使用Daubechies,、 Coieflet,、Symlets和Biorthogonal系小波對加噪HMM-ESD電流波形進行2~8層分解，統(tǒng)一采用Stein無偏估計原則閾值和軟門限閾值方式處理后,，計算小波去噪后信號較純凈信號的SNR和MSE,。為了便于觀察小波函數階次和分解層次對去噪性能的影響，圖5給出了Symlets小波系不同階次小波函數和分解層次下SNR和MSE的變化趨勢,。

    圖5(a)展示了Symlets小波去噪分析的SNR趨勢,，總體上看，隨著sym小波函數階次N的增加,，SNR增大,，但是較高階次的小波函數間的去噪性能差距并不明顯；分解層次多集中在4~6層附近時,，SNR相對較大。圖5(b)展示了Symlets小波去噪分析的MSE趨勢,，總體上看,， MSE與 SNR呈相反的變化趨勢。因此,，在實測ESD電流波形的小波去噪處理中,，應盡量選取高階次的小波函數和4~6層分解進行小波分析。為了獲悉不同小波系函數對加噪ESD電流波形的降噪效果,，表1給出了各小波系中去噪性能較好的部分性能參數,。

    表1中,，小波函數db9、sym4,、sym6,、sym7對應的信噪比在 48.6 dB以上，相對于其他小函數去噪效果較好,。其中,，sym7小波函數去噪效果最佳。整體上看,，使用Symlets系列小波函數對含噪ESD電流信號做去噪分析較為適宜,。

4 實測ESD電流波形去噪

    針對圖3所示40 GHz采樣頻率的6 kV ESD電流波形，選取sym7小波函數作為母小波對其進行5層分解,，分解后的近似信息（A5）和細節(jié)信息（D1~D5）如圖6所示,。

    圖6中，第一層小波系數（D1）幅值分布較為均勻,，基本不含有用信息,。因此，可以將該層小波系數置零,，其他各層小波系數采用Stein無偏估計原則閾值做軟門限閾值處理,。小波閾值去噪處理后的ESD電流波形如圖7所示，與圖3所示的實測ESD電流波形相比,，噪聲毛刺明顯減少,。

    使用Sage-Husa自適應Kalman濾波算法對小波預處理后的ESD電流數據做優(yōu)化處理，獲得如圖8所示電流波形,。該電流波形與圖7小波去噪后的ESD電流波形相比,，電流波形中寄生振蕩的噪聲有所削減，整體光滑度更好,。

5 結論

    本文將小波分析與自適應卡爾曼濾波算法相結合,，應用于ESD電流波形的去噪分析。并使用Adams預測校正算法結合Runge-Kutta算法數值計算HMM-ESD電流值,，建立了含噪ESD電流信號模型,。通過統(tǒng)一閾值選取方式和閾值處理方法，分析了不同小波函數在不同分解層次的去噪性能,。結果顯示,，較高階次的小波函數在4~6層分解時對ESD電流信號的去噪效果較好。對于實測ESD電流波形,，在小波閾值去噪的基礎上,，引入Sage-Husa自適應Kalman濾波算法做優(yōu)化處理，獲得了更好的去噪效果。

參考文獻

[1] 陳硯橋,，劉尚合,，武占成，等.靜電放電電磁脈沖的實驗研究[J].強激光與粒子束,，1999,，11(3)：359-362.

[2] 賀其元，劉尚合,，孫國至,，等.ESD發(fā)生器開關動作對抗擾度試驗的影響[J].高電壓技術，2007,，33(6)：93-96.

[3] IEC 61000-4-2,，Electromagnetic compatibility(EMC)-Part 4-2：Testing and measurement techniques-Electrostatic discharge immunity test[S].2008.

[4] 李田科，劉輝,，王亮,，等.基于小波變換的自適應Kalman濾波算法研究[J].兵工自動化，2013,，32(1)：32-35.

[5] 杜浩藩,，叢爽.基于MATLAB小波去噪方法的研究[J].計算機仿真，2003,，20(7)：119-122.

[6] 陳翔,，魏明，王雷,，等.人體-金屬模型靜電放電電流波形小波去噪[J].高壓電器,，2010，46(8)：14-17.

[7] SAGE A P,，HUSA G W.Adaptive filtering with unknown prior statistics[C].Proceedings of Joint Automatic Control Conference,，1969：760-769.

[8] RUNG F M，GAO Y G,，F(xiàn)UJIWARA O.Voltage dependence property of parameters for human body discharge in air through a small metal rod[J].The Journal of China Universities of Posts and Telecommunications,，2008，15(4)：86-90.

[9] 汪軻,，汪金山,，汪曉東.基于5階HMM-ESD電流表達式及頻譜分析[C].第二十九屆中國控制會議論文集，2010：890-893.

[10] 朱長青,，劉尚合,，魏明.ESD電流的解析表達式與數值解[J].高電壓技術，2005,，31(7)：22-24.

[11] 朱長清,，劉尚合，魏明.靜電放電模擬器放電回路的設計[J].儀表技術與傳感器,，2004(3)：31-33.

[12] ZHOU K,，RUAN F M.HMM-ESD current calculation based on adams prediction-calibration method[C].The 5th International Symposium on Electromagnetic Compatibility Proceedings，2017：261-265.

作者信息：

周  奎1,，2,，阮方鳴2，3,，管  勝1,，蘇  明3，王  珩3

（1.貴州大學 大數據與信息工程學院,，貴州 貴陽550025,；2.北京東方計量測試研究所，北京100094,；

3.貴州師范大學 大數據與計算機科學學院,，貴州 貴陽550001）