0 引言

    在高頻電磁問(wèn)題中,，一致性幾何繞射理論（UTD）應(yīng)用非常廣泛^[1],，例如目標(biāo)散射特性預(yù)估。因此,，在準(zhǔn)確獲得目標(biāo)表面UTD繞射場(chǎng)問(wèn)題上,，表面爬行射線波追蹤起著非常大的作用^[2]。所以,，首先要進(jìn)行目標(biāo)表面爬行波追蹤（測(cè)地線軌跡）,。但是，實(shí)際上除了一些典型形體能夠直接得到測(cè)地線微分方程（GDE）外,，在任意形狀的光滑物體表面如何測(cè)定測(cè)地線軌跡是一個(gè)巨大的挑戰(zhàn),。

    JHA R M^[3-5]提出了Geodesic Constant解析方法，但只在一般的拋物旋轉(zhuǎn)面適用,。通常地,，在工程應(yīng)用上，很多目標(biāo)被看作如木板,、圓柱,、圓錐和球等一些已經(jīng)有爬行波尋跡解析解的典型形體。但很難用這些典型形體去估計(jì)復(fù)雜形體,，這似乎就限制了UTD方法的應(yīng)用,。

    因此，需要介紹一下數(shù)值爬行波追蹤算法，該方法基于離散三角面剖分模型表面,，但是不能直接應(yīng)用于UTD算法^[6],。除了用離散三角形面片建立復(fù)雜模型，它還可以描述NURBS曲面,。而且,，NURBS曲面由于它的高精度、少面片的特性,，被引用到高頻電磁分析領(lǐng)域,。當(dāng)目標(biāo)用NURBS曲面表示后，測(cè)地線軌跡可由GDE求解直接獲得,。所以,，一些數(shù)值方法被用來(lái)計(jì)算GDE。為了獲得NURBS曲面上的爬行波軌跡^[7],，歐拉方法效率高但是精度低,，精度依賴于剖分面片外形，對(duì)于任意形狀模型可能會(huì)失效,。

    為了提高在任意形狀NURBS表面爬行波追蹤的準(zhǔn)確性和效率,，本文提出了一種基于新型自適應(yīng)變步長(zhǎng)歐拉法的爬行波跟蹤算法。由于自適應(yīng)變步長(zhǎng)歐拉方法是基于傳統(tǒng)的歐拉法,，從而保證了效率,；并在數(shù)值迭代求解GDE的過(guò)程中引進(jìn)形狀因子ξ，離散的步長(zhǎng)可以及時(shí)自適應(yīng)地糾正,。因此,，與傳統(tǒng)的歐拉法相比，該方法可以很容易地保證其準(zhǔn)確性在任意形狀的NURBS表面上的爬行光線跟蹤,。也就是說(shuō),，它更適合于工程應(yīng)用。

1 任意形狀目標(biāo)NURBS曲面建模

    非均勻有理B樣條(Non-Uniform Rational B-Splines,，NURBS)曲面是非均勻B樣條曲面的有理推廣,。它被定義為：

    u、v參數(shù)域映射到3個(gè)空間可以在圖1中看到,。

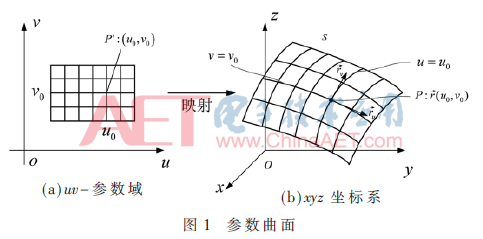
    下面在圖2中給出3個(gè)NURBS建模結(jié)果,。其中圓柱的表面是均勻網(wǎng)格表面，而其他表面是不均勻網(wǎng)格表面,。

2 任意NURBS曲面表面的爬行波追蹤算法

    對(duì)于源點(diǎn)和觀察點(diǎn)的位置,，光滑曲面表面的繞射問(wèn)題有3種類型：(1)源點(diǎn)和觀察點(diǎn)都不在表面且遠(yuǎn)離表面，這種情況屬于光滑曲面散射問(wèn)題,；(2)源點(diǎn)在曲面上,，觀察點(diǎn)遠(yuǎn)離表面，此時(shí)為光滑曲面輻射問(wèn)題；(3)源點(diǎn)與觀察點(diǎn)都在表面上,，這就屬于耦合問(wèn)題^[10],。

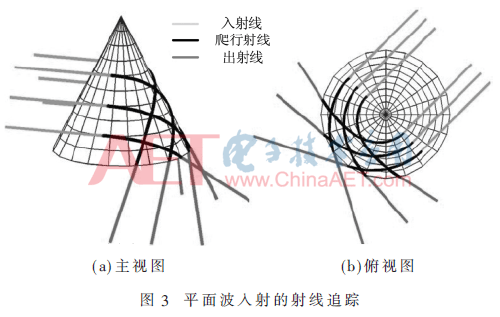
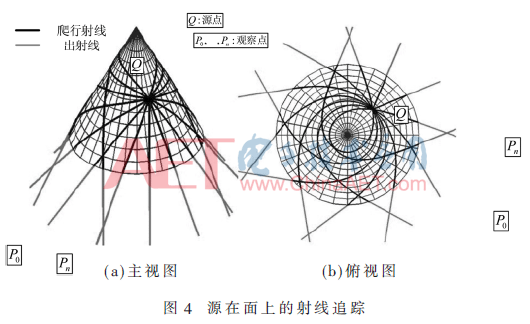
    所以,，射線追蹤也有3種類型,，根據(jù)圖3～圖5所示，在所有這些情況下,，表面上的射線軌跡稱為爬行波,，其被約束沿著測(cè)地線傳播。本文主要關(guān)注爬行波的射線追蹤,，因?yàn)樗巧渚€追蹤過(guò)程中最困難的一部分,。

2.1 爬行波的入射點(diǎn)和出射點(diǎn)

    根據(jù)這兩個(gè)方程可以求解出NURBS曲面上大量的入射點(diǎn)與出射點(diǎn)。

2.2 基于自適應(yīng)變步長(zhǎng)歐拉法求解射線追蹤GDE

    由于任意形狀的表面上的爬行射線的路徑滿足GDE,，因此可以將爬行射線的問(wèn)題改為求解GDE的問(wèn)題,。一般來(lái)說(shuō)，通過(guò)歐拉法求解GDE是一種簡(jiǎn)單快捷的方法,。但是根據(jù)研究,，在大多數(shù)情況下由于傳統(tǒng)的歐拉法精度低，穩(wěn)定性不好,，導(dǎo)致求解效果不好,。

    對(duì)于非線性問(wèn)題，基本上需要步進(jìn)控制校正程序,。因此,，本文中，為提高光線跟蹤的準(zhǔn)確性并確保效率,，提出了自適應(yīng)變步長(zhǎng)歐拉方法來(lái)求解GDE,。

    GDE方程如下：

其中，h是兩個(gè)相鄰離散點(diǎn)之間的步長(zhǎng),，并且確定它是非常重要的,。ξ是形狀因子（SF），用來(lái)自適應(yīng)地控制每個(gè)離散步長(zhǎng),。而ξ的值受制于對(duì)象的形狀,，關(guān)于ξ的更多細(xì)節(jié)將在2.3節(jié)中給出。

    在數(shù)值計(jì)算中,，可以計(jì)算多個(gè)離散點(diǎn)(u_i,，v_i)來(lái)表示爬行波，i=0,，1,，2…。因此，根據(jù)離散化,，上式可以重寫(xiě)為：

    由式(13)可知,，(u_i+2，v_i+2)能用(u_i+1,，v_i+1),、(u_i，v_i)及ξ_i+1,，i推導(dǎo)而出,。必須計(jì)算出爬行射線最初的兩個(gè)坐標(biāo)(u₀，v₀),、(u₁,，v₁)及ξ_1，0,，才能遞推出整個(gè)爬行射線,。

    可以通過(guò)方程(4)獲得第一個(gè)點(diǎn)Q₀(u₀，v₀),，然后由微分幾何,，第二個(gè)點(diǎn)可由Q₀在u，v各自方向切向量之和近似表示,，如圖7所示,。

    這里第二個(gè)點(diǎn)表示為：

    形狀因子的一般表達(dá)式在2.3節(jié)中給出。根據(jù)表達(dá)式,，可以確定得到ξ_1,，0。計(jì)算出(u₀,，v₀),、(u₁，v₁)及ξ_1,，0后,，(u_i，v_i)可以根據(jù)式(12)隨著i的增加逐步迭代算出,。

2.3 形狀因子?孜的推導(dǎo)

    微分方程的精度與步長(zhǎng)h有關(guān),，步長(zhǎng)越小精度越高。然而,，在迭代求解爬行波射線軌跡上的離散點(diǎn)的過(guò)程中,，算法效率因離散點(diǎn)數(shù)的增加而減小，而且,，離散點(diǎn)越多,，累積誤差越大,，可能導(dǎo)致錯(cuò)誤的結(jié)果。

    顯然,，為了逼近如果在變量變化快的區(qū)域多取離散點(diǎn)而在變化慢區(qū)域少取離散點(diǎn),，就可以在保證計(jì)算效率的同時(shí)兼顧精度，所以合理提取離散點(diǎn)是很重要的,。

    但是在實(shí)際情況中,，無(wú)法得知確定的(u(s)，v(s))表達(dá)式,，所以導(dǎo)致離散點(diǎn)無(wú)法合理提取,。于是本文提出用形狀因子ξ來(lái)反映參數(shù)變化,，用于確定離散步長(zhǎng),。用ξ的離散值ξ_i+1，i來(lái)表示爬行射線相鄰點(diǎn)參數(shù)變化率,。ξ_i+1,，i的表達(dá)式如下：

    設(shè)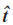為曲線C上P點(diǎn)處的單位切向量。P點(diǎn)處的離散編號(hào)為i,。

    對(duì)方程(17)中的變量s求微分,，可得單位切向量：

3 數(shù)值算例與分析

    理論上可以在一些典型物體（如圓柱體、錐體）上計(jì)算爬行射線,，因此,，可以從這些對(duì)象的分析結(jié)果中驗(yàn)證所提出的方法是否有效。

3.1 圓柱體

    圖9所示為圓柱表面（均勻網(wǎng)格）爬行波射線傳播軌跡圖,。圓柱的半徑為1 m,，高為3 m。表1為爬行波尋跡結(jié)果,，起始點(diǎn)為(1,，0，0),。

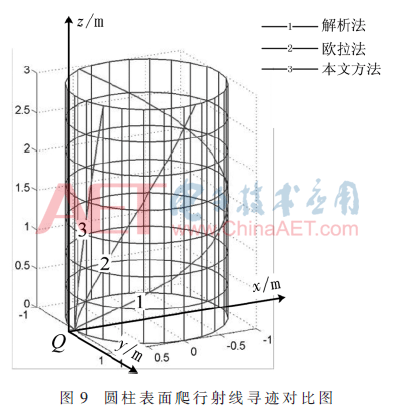
    從表1可知,，采用自適應(yīng)變步長(zhǎng)歐拉法得到的數(shù)值結(jié)果與解析方法的結(jié)果吻合得非常好，由此可證明該尋跡算法正確性,。

3.2 任意曲面目標(biāo)

    圖10所示為任意曲面表面（非均勻網(wǎng)格表面）爬行波射線傳播軌跡圖,。根據(jù)微分幾何知識(shí)，球面上的數(shù)值結(jié)果可以直接由理論值得到驗(yàn)證,。表2為爬行波尋跡結(jié)果,，起始點(diǎn)為(1.0，0.0,，0.0),。

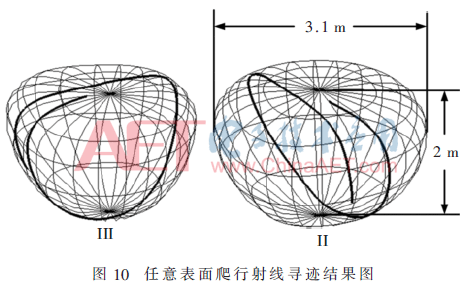
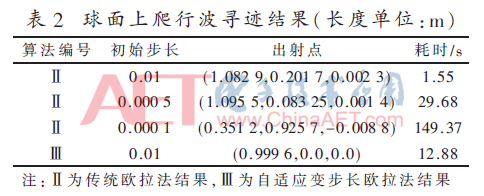
    如圖10所示,，提出的方法結(jié)果與理論結(jié)果吻合較好。從表2和圖10可以看出,，盡管隨著離散步長(zhǎng)的增加歐拉方法的誤差減少了,，但是耗時(shí)也增加了很多。更重要的是,，如果離散步長(zhǎng)繼續(xù)增加下去,，結(jié)果完全錯(cuò)誤，這意味著歐拉方法不穩(wěn)定,。

4 結(jié)論

    對(duì)于任意形狀NURBS目標(biāo)表面爬行波射線軌跡尋跡,，本文提出了基于自適應(yīng)變步長(zhǎng)歐拉法的快速有效的尋跡算法。為了驗(yàn)證該尋跡算法的正確性與有效性,，給出了幾個(gè)典型驗(yàn)證算例,。相比于傳統(tǒng)的歐拉法，自適應(yīng)變步長(zhǎng)歐拉法不僅繼承了傳統(tǒng)歐拉法的效率高的優(yōu)勢(shì),，而且該算法適用于任意的光滑曲面,。

參考文獻(xiàn)

[1] PATHAK P H，BURNSIDE W D,，MARHEFKA R J.A uniform GTD analysis of the diffraction of electromagnetic waves by a smooth convex surface[J].IEEE Transactions on Antennas and Propagation,，1980，28(5)：631-642.

[2] JHA R M,，WIESBECK W.The geodesic constant method：a novel approach to analytical surface-ray tracing on convex conducting bodies[J].IEEE Antennas and Propagation Magazine,，1995，37(5)：28-38.

[3] SURAZHSKY V,，SURAZHSKY T,，KIRSANOV D，et al.Fast exact and approximate geodesics on meshes[J].ACM Transactions on Graphics,，2005,，24(3)：553-560.

[4] JHA R M，BOKHARI S A.A novel ray tracing on general paraboloids of revolution for UTD applications[J].IEEE Antennas and Propagation Magazine,，1993,，41(7)：934-939.

[5] PEREZ J，CATEDRA M F.RCS of electrically large targets modeled with NURBS surfaces[J].Electronics Letters,，1992,，28(12)：1119-1122.

[6] PEREZ J，CATEDRA M F.Application of physical optics to the RCS computation of bodies modeled with NURBS surfaces[J].IEEE Transactions on Antennas and Propagation,，1994,，42(2)：1404-1411.

[7] 李坤，劉濤,，王永建,，等.基于小波變換的電力線通信信號(hào)識(shí)別研究[J].電子技術(shù)應(yīng)用,，2016，42（6）：113-120.

[8] BOCHM W.Generating the Bezier points of b-spline curves and surfaces[J].Computer Aided Design,，1981,，13(16)：365-366.

[9] Fu Song，Zhang Yunhua,，He Siyuan,，et al.Creeping ray tracing algorithm for arbitrary NURBS surfaces based on adaptive variable step Euler method[J].International Journal of Antennas and Propagation，2015(5)：1-12.

[10] 付松.介質(zhì)涂覆目標(biāo)表面爬行波尋跡及其電磁繞射建模方法研究[D].武漢：武漢大學(xué),，2015.

作者信息:

曹  拓,，付  松，何思遠(yuǎn)

（武漢大學(xué) 電子信息學(xué)院,，湖北 武漢430072）