文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.174930
中文引用格式: 程玉柱,李趙春. 基于改進(jìn)的Bingham模型的圖像去噪算法[J].電子技術(shù)應(yīng)用,2018,44(6):72-75.
英文引用格式: Cheng Yuzhu,Li Zhaochun. Image denoising algorithm based on improved Bingham model[J]. Application of Elec-
tronic Technique,2018,44(6):72-75.
0 引言
磁流變阻尼器是應(yīng)用磁流變液在強(qiáng)磁場(chǎng)下快速可逆流變特性而制造出的一種有著廣泛應(yīng)用前景的減振控制裝置[1]。由于磁流變阻尼器的非線性,建立較為精確的阻尼器動(dòng)力學(xué)模型是開(kāi)發(fā)和使用阻尼器獲得好的控制效果的關(guān)鍵因素之一[2]。磁流變液的流體力學(xué)性能受到外加磁場(chǎng)等多因素影響,本構(gòu)關(guān)系復(fù)雜,難以建立精確的數(shù)學(xué)模型,目前還沒(méi)有統(tǒng)一的磁流變阻尼器力學(xué)模型[3]。
Bingham模型是一種常用的磁流變阻尼器塑性流體力學(xué)模型[4]。Herschel-Bulkley模型是一種改進(jìn)的非線性Bingham模型,具有冪律的本構(gòu)關(guān)系,其整數(shù)階導(dǎo)數(shù)模型需要引入多個(gè)導(dǎo)數(shù)項(xiàng)和材料參數(shù)[5]。分?jǐn)?shù)階導(dǎo)數(shù)可以很好地描述具有冪律的復(fù)雜非線性自然和社會(huì)現(xiàn)象[6]。為此,本文將分?jǐn)?shù)階微分和Bingham模型相結(jié)合,得到分?jǐn)?shù)階Bingham模型,描述磁流變阻尼器的動(dòng)力學(xué)過(guò)程。
圖像去噪是圖像預(yù)處理的重要步驟[7],基于偏微分方程(PDE)的圖像去噪方法是圖像分析和處理的研究熱點(diǎn)[8]。本文由分?jǐn)?shù)階Bingham模型推導(dǎo)得到分?jǐn)?shù)階Bingham PDE圖像去噪模型,并定義一種分?jǐn)?shù)階邊緣檢測(cè)算子,用于圖像去噪。試驗(yàn)結(jié)果證明了算法的有效性。
1 分?jǐn)?shù)階微積分與Bingham模型
1.1 分?jǐn)?shù)階微積分定義
分?jǐn)?shù)階微積分是數(shù)學(xué)分析的一個(gè)重要分支,目前分?jǐn)?shù)階微積分有多種定義表達(dá)式[9],其中主要有3種經(jīng)典的時(shí)域表達(dá)式,包括Grümwald-Letnikov、Riemann-Liouville 和Capotu定義,3種定義在一定條件下是等價(jià)的。分?jǐn)?shù)階微積分的定義為:

式中,v為分?jǐn)?shù)階數(shù),G表示G-L定義,下標(biāo)a和t表示積分式的下界和上界,a為時(shí)間t的初值。
1.2 Bingham模型
Bingham模型是磁流變阻尼器常采用的力學(xué)模型之一,其應(yīng)力與應(yīng)變的關(guān)系為:

1.3 Herschel-Bulkley模型
Herschel-Bulkley模型是一種改進(jìn)的Bingham模型,能夠解釋磁流變液屈服后剪切稀化和剪切增稠行為。其模型表達(dá)式為:

2 分?jǐn)?shù)階Bingham磁流變阻尼器力學(xué)模型
Herschel-Bulkley模型是一種整數(shù)階導(dǎo)數(shù)模型,式(3)具有冪律特性,其應(yīng)力與應(yīng)變響應(yīng)依賴于時(shí)間和應(yīng)變率,與載荷和變形歷史有關(guān),具有記憶性。相比Bingham模型,它引入了多個(gè)導(dǎo)數(shù)項(xiàng)和材料參數(shù),較準(zhǔn)確地描述了磁流變液的動(dòng)力學(xué)特性。針對(duì)模型的冪率特性,Gemant[4]建議將分?jǐn)?shù)階時(shí)間導(dǎo)數(shù)引入到材料的本構(gòu)關(guān)系中,能用較少的材料參數(shù)便能準(zhǔn)確地描述大量復(fù)雜的具有記憶性的材料的動(dòng)力學(xué)特性。為此,將式(1)的分?jǐn)?shù)階引入到式(2)當(dāng)中,提出一種分?jǐn)?shù)階Bingham磁流變阻尼器力學(xué)模型,如式(4)所示。

3 分?jǐn)?shù)階Bingham圖像去噪模型
3.1 圖像去噪模型

再令u(0)=u0為初始含噪圖像,得到PDE圖像去噪迭代模型:

3.2 數(shù)值解法
數(shù)值解法采用有限差分方法。將圖像看成向量[1×MN],向量元素ui為像素灰度值,i∈[1,…,MN],h表示離散網(wǎng)格大小,tk=τk為離散時(shí)間,其中k為正整數(shù),τ為時(shí)間步長(zhǎng)。對(duì)圖像進(jìn)行時(shí)域微分:

得到分?jǐn)?shù)階微分掩模算子[11],即Tainsi算子,如圖1所示。利用Tainsi算子對(duì)式(11)作分?jǐn)?shù)階微分處理,得到一種分?jǐn)?shù)階邊緣檢測(cè)算子。
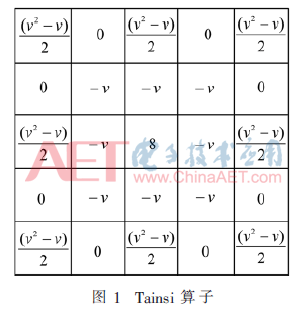
4 試驗(yàn)結(jié)果
4.1 性能評(píng)價(jià)
圖像去噪結(jié)果評(píng)價(jià)采用的評(píng)價(jià)測(cè)度方法有兩種[12-13],即信噪比(SNR)和平均結(jié)構(gòu)相似度(MSSIM)。SNR圖像去噪評(píng)價(jià)采用式(17):

式中,M為局域窗口數(shù)目,X、Y為參考標(biāo)準(zhǔn)和去噪圖像。
4.2 結(jié)果
對(duì)人工合成圖像進(jìn)行去噪,并比較不同階數(shù)(0≤v≤1)的圖像去噪算法處理結(jié)果,如圖2所示。圖2(a)大小為150×150;噪聲圖像圖2(b)的SNR為7.966 5,噪聲σ=10;圖2(c)~(f)分別為分?jǐn)?shù)階數(shù)為0、0.3、0.7、1,迭代次數(shù)為40的圖像去噪結(jié)果。從圖中看出,當(dāng)階數(shù)為0.7時(shí),圖像去噪效果最好,既保持了邊緣,又去除了噪聲。式(6)中v1和v2取不同值,用分?jǐn)?shù)階Bingham圖像去噪模型式(7)對(duì)圖2(b)去噪,得到SNR和MSSIM值,如表1所示。當(dāng)v1=v2=0.7時(shí),SNR最大;當(dāng)v1=v2=0.5 時(shí),MSSIM最大。


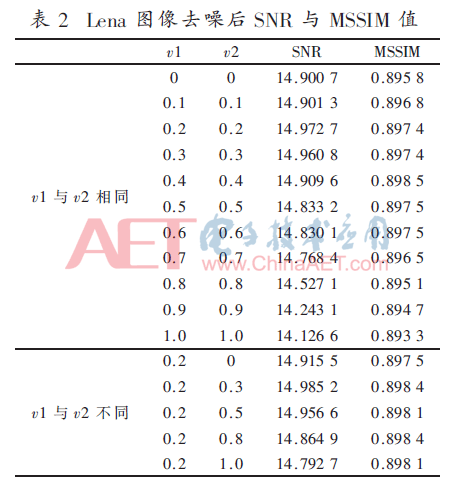
對(duì)Lena圖像進(jìn)行去噪,并比較不同階數(shù)(0≤v≤1)圖像去噪算法處理結(jié)果,如圖3所示。圖3(a)大小為256×256,噪聲圖像3(b)的SNR為12.653 1,噪聲σ=10,圖3(c)~(f)分別為分?jǐn)?shù)階數(shù)為0、0.3、0.7、1,迭代次數(shù)為10的圖像去噪結(jié)果。從圖中看出,當(dāng)階數(shù)為0.3時(shí),圖像去噪效果最好,既保持了邊緣,又去除了噪聲。式(6)中v1和v2取不同值,用分?jǐn)?shù)階Bingham圖像去噪模型式(7)對(duì)圖3(b)去噪,得到SNR和MSSIM值,如表2所示。當(dāng)v1=0.2、v2=0.3時(shí),SNR最大;當(dāng)v1=v2=0.4 時(shí),MSSIM最大。

4.3 算法分析
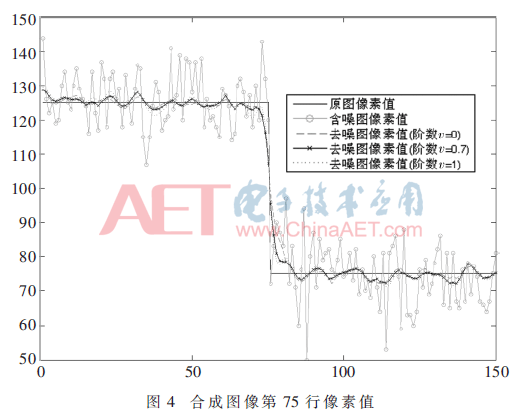
提取圖2中的第75行像素值,如圖4所示,圖中包括無(wú)噪像素值、含噪圖像素值、不同階數(shù)(v=0、0.7、1)的去噪圖像素值。從圖看出,在平坦區(qū)域,當(dāng)v=0.7時(shí)像素值更接近真實(shí)值,當(dāng)v=1.0時(shí)像素值振蕩幅度最大,去噪效果最差;在邊緣區(qū)域,當(dāng)v=1.0時(shí)邊緣保持效果最好,v=0.7次之,v=0最差;綜合比較,當(dāng)v=0.7時(shí),分?jǐn)?shù)階Bingham力學(xué)模型效果最好,既保持了圖像高頻邊緣信息,又抑制了低頻區(qū)域噪聲,此現(xiàn)象與表1數(shù)值表現(xiàn)一致。表1和表2中,SNR與MSSIM的峰值位置距離較近,且SNR與MSSIM的數(shù)值變化趨勢(shì)保持一致,從而證明選擇合適的分?jǐn)?shù)階數(shù)確能改善Bingham力學(xué)模型圖像去噪效果。
5 結(jié)論
圖像去噪是圖像處理中最基本問(wèn)題之一,既實(shí)現(xiàn)去噪又保持圖像邊緣高頻信息是圖像去噪的重要目標(biāo)。本文利用Bingham磁流變阻尼器力學(xué)模型與分?jǐn)?shù)階微積分原理相結(jié)合,提出一種分?jǐn)?shù)階磁流變阻尼器力學(xué)圖像去噪模型,MATLAB試驗(yàn)結(jié)果表明:
(1)根據(jù)Bingham磁流變阻尼器力學(xué)模型,對(duì)剪切應(yīng)變率作分?jǐn)?shù)階處理,推導(dǎo)得到分?jǐn)?shù)階Bingham圖像去噪模型是有效的。
(2)定義的分?jǐn)?shù)階邊緣檢測(cè)算子及分?jǐn)?shù)階掩模算子(Tainsi算子)是可行的,能有效檢測(cè)圖像邊緣,具有較好抗噪性能。
(3)通過(guò)選擇合適的分?jǐn)?shù)階階數(shù),能夠優(yōu)化圖像去噪效果,既能保持圖像邊緣信息,又能較好實(shí)現(xiàn)圖像去噪。
參考文獻(xiàn)
[1] 郭迎慶,徐趙東,費(fèi)樹(shù)岷,等.磁流變智能結(jié)構(gòu)的微粒群優(yōu)化控制[J].振動(dòng)與沖擊,2011,30(9):59-63.
[2] WANG D H,LIAO W H. Magnetorheological fluid dampers:a review of parametric modelling[J].Smart Materials and Structures,2011,20(2):3001.
[3] 朱莉.增益映射耦合局部正則化的圖像重構(gòu)算法[J].電子技術(shù)應(yīng)用,2016,42(3):127-131.
[4] CARLSON J D,JOLLY M R.MR fluid,foam and elastomer devices[J].Mechatronics,2000,10(5):55-69.
[5] WANG X,GORDANINEJAD F. Flow analysis of field-controllable,electro and magneto-rheological fluids using Herschel-Bulkley model[J].Journal of Intelligent Material Systems & Structures,1999,10(8):601-608.
[6] 陳文,孫洪廣,李西成,等.力學(xué)與工程問(wèn)題的分?jǐn)?shù)階導(dǎo)數(shù)建模[M].北京:科學(xué)出版社,2010.
[7] CHAN T F,Shen Jianghong.Image proecssing and analysis varitional,PDE,wavelet and stochastic methods[M].Society for Industrial and Applied Mathematics,2005.
[8] 宋錦萍,陳花竹,臺(tái)雪成.一種PDE圖像分解去噪模型及算法[J].中國(guó)圖象圖形學(xué)報(bào),2009,14(8):1547-1552.
[9] 黃果,許黎,蒲亦非.分?jǐn)?shù)階微積分在圖像處理中的研究綜述[J].計(jì)算機(jī)應(yīng)用研究,2012,29(2):414-420.
[10] Pu Yifei,Zhou Jiliu,Yuan Xiao.Fractional differential mask: a fractional differential-based approach for multiscale texture enhancement[J].IEEE Transctions on Image Processing,2010,19(2):491-511.
[11] 楊柱中,周激流,黃梅,等.基于分?jǐn)?shù)階微分的邊緣檢測(cè)[J].四川大學(xué)學(xué)報(bào)(工程科學(xué)版),2008,40(1):152-157.
[12] GONZALEZ R C,WOODS R E.Digital image processing(2nd ed)[M].Upper Saddle River:Prentice Hall,2001.
[13] WANG Z. BOVIK A,SHEIKH H,et al.Image quality assessment: from error visibility to structural simiilarity[J].IEEE Transctions on Image Processing,2004,13(4):600-612.
作者信息:
程玉柱,李趙春
(南京林業(yè)大學(xué) 機(jī)械電子工程學(xué)院 測(cè)控技術(shù)系,江蘇 南京210037)

