文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.172555
中文引用格式: 周應(yīng)超,黃瓊,申濱. 基于內(nèi)波束干擾消除的大規(guī)模MIMO低復(fù)雜度波束成形[J].電子技術(shù)應(yīng)用,2017,43(8):16-20.
英文引用格式: Zhou Yingchao,Huang Qiong,Shen Bin. Low-complexity beamforming based on inter-beam interference cancellation for massive MIMO[J].Application of Electronic Technique,2017,43(8):16-20.
0 引言
在最近幾年時(shí)間里,大規(guī)模MIMO技術(shù)得到了廣泛的重視與研究,并被認(rèn)為是第五代移動(dòng)通信系統(tǒng)中的關(guān)鍵技術(shù)之一[1-3]。大規(guī)模MIMO的主要優(yōu)點(diǎn)體現(xiàn)在降低發(fā)射功率、提升能量效率并采用多址接入和復(fù)用增益大幅提升頻譜效率[4]。大規(guī)模MIMO系統(tǒng)利用其提供的空間自由度能在不增加時(shí)頻資源的情況下在同一時(shí)頻資源上向多個(gè)用戶發(fā)送信號(hào)[5],其波束成形技術(shù)能有效抑制多址干擾,是其物理層中的關(guān)鍵技術(shù)之一,其中研究較多的傳統(tǒng)波束成形,如最小均方誤差(Minimun Mean Square Error,MMSE)[6-7]波束成形和奇異值分解(Singular-Value Decomposition,SVD)[8-9]波束成形,因其帶來(lái)的高計(jì)算復(fù)雜度,限制了其在實(shí)際中的應(yīng)用。在商業(yè)無(wú)線網(wǎng)絡(luò)中降低部署大規(guī)模MIMO系統(tǒng)時(shí)的實(shí)施復(fù)雜度是非常值得關(guān)注的,最大比傳輸(Maximum Ratio Transmission,MRT)[10]波束成形和迫零波束成形(Zero-Forcing beamforming,ZFBF)[11-12]因?qū)嵤┹^簡(jiǎn)單,被廣泛應(yīng)用于大規(guī)模MIMO系統(tǒng)。其中MRT復(fù)雜度最低,是實(shí)施起來(lái)最簡(jiǎn)單的波束成形算法,但其缺點(diǎn)為存在用戶間干擾,和速率性能明顯劣于其他波束成形技術(shù),即使利用合適的用戶選擇技術(shù)也難以避免用戶間干擾的問(wèn)題。ZFBF則可以完全消除用戶間的內(nèi)波束干擾,提供較高的和速率性能,但其計(jì)算復(fù)雜度較MRT也高出許多。利用迭代QR分解(QRD)計(jì)算ZFBF的波束成形矩陣能降低其計(jì)算復(fù)雜度[12],然而文獻(xiàn)[12]中的QRD考慮的場(chǎng)景是用戶端全復(fù)用情況下能降低ZFBF的計(jì)算復(fù)雜度。當(dāng)用戶端不是進(jìn)行全復(fù)用時(shí),QRD則需要額外的運(yùn)算操作,從而進(jìn)一步增大其計(jì)算復(fù)雜度。因此在大規(guī)模MIMO系統(tǒng)中,當(dāng)用戶端復(fù)用不全時(shí),基于QRD的ZFBF要求的計(jì)算復(fù)雜度會(huì)高于傳統(tǒng)ZFBF。
本文提出一種基于部分內(nèi)波束干擾消除的低復(fù)雜度BF算法,考慮消除部分用戶間的內(nèi)波束干擾,以此來(lái)實(shí)現(xiàn)計(jì)算復(fù)雜度與和速率性能之間的良好折衷。假定用戶間的內(nèi)波束干擾大小不相等,為了降低計(jì)算復(fù)雜度,考慮只消除一些數(shù)值大的內(nèi)波束干擾。為此,首先通過(guò)傳統(tǒng)MRT技術(shù)生成用戶的波束成形矢量,然后計(jì)算用戶間內(nèi)波束干擾量,再通過(guò)內(nèi)波束干擾消除算法的一系列矢量運(yùn)算,去除一部分干擾量大的強(qiáng)干擾,以此避開(kāi)復(fù)雜的高維度矩陣運(yùn)算和矩陣求逆,因而能達(dá)到計(jì)算復(fù)雜度與和速率間的良好折衷。
1 大規(guī)模MIMO系統(tǒng)模型
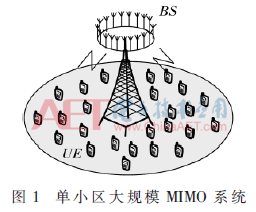
圖1所示為大規(guī)模MIMO的下行鏈路,基站端部署了N根天線,可在同一時(shí)頻資源中與用戶集ΩM中的M個(gè)單天線用戶通信,且N≥M。假設(shè)環(huán)境模式是時(shí)分雙工(Time Division Duplex,TDD)模式,信道衰落為平坦瑞利衰落,基站端天線可以獲得完整的信道狀態(tài)信息(Channel State Information,CSI)。


2 內(nèi)波束干擾消除算法
傳統(tǒng)波束成形技術(shù),如文獻(xiàn)[6,7]和文獻(xiàn)[8,9]中的MMSE和SVD發(fā)送信號(hào)時(shí),其和速率性能接近最優(yōu)波束成形,但其計(jì)算復(fù)雜度過(guò)高,都不便于在實(shí)際中實(shí)施。因此,為了大幅度降低計(jì)算復(fù)雜度同時(shí)保持和速率損失較小,本節(jié)提出了基于部分內(nèi)波束干擾消除的低復(fù)雜度BF算法。
發(fā)端利用MMSE目的是最小化發(fā)送符號(hào)與接收符號(hào)的均方誤差(Mean Square Error,MSE):

2.1 算法設(shè)計(jì)
傳統(tǒng)波束成形技術(shù),如文獻(xiàn)[10]中的MRT和文獻(xiàn)[11,12]中的ZFBF,因其便于實(shí)際中的實(shí)施和良好的和速率性能,被廣泛應(yīng)用于多用戶信號(hào)傳輸。MRT和ZFBF的波束成形矩陣表達(dá)式如下:

且提供較優(yōu)的和速率,但其計(jì)算復(fù)雜度較高,在大規(guī)模MIMO環(huán)境中較難實(shí)施。文獻(xiàn)[12]中提出利用QRD可以降低ZFBF的復(fù)雜度,但當(dāng)用戶端不是進(jìn)行全復(fù)用時(shí),基于QRD的ZFBF需要增加額外的運(yùn)算操作,產(chǎn)生的復(fù)雜度會(huì)高于傳統(tǒng)ZFBF。
為便于實(shí)際中應(yīng)用波束成形技術(shù),考慮降低多用戶波束成形的計(jì)算復(fù)雜度,同時(shí)顯著降低來(lái)自其他用戶對(duì)目標(biāo)用戶的內(nèi)波束干擾,以此達(dá)到大幅度提高和速率的目的。考慮MRT場(chǎng)景下確定的波束矢量w,其會(huì)受到其他用戶的干擾。為了緩解其他用戶對(duì)目標(biāo)用戶的內(nèi)波束干擾,提高和速率性能,同時(shí)考慮實(shí)現(xiàn)的復(fù)雜性,本文采用內(nèi)波束干擾消除算法,考慮消除每個(gè)用戶對(duì)其他M-1個(gè)用戶造成的內(nèi)波束干擾中數(shù)值較大的S個(gè)強(qiáng)干擾,為平衡計(jì)算復(fù)雜度與和速率間的良好折衷,數(shù)值S可以預(yù)先確定。
來(lái)自用戶i對(duì)用戶k的內(nèi)波束干擾量的大小為:


2.2 復(fù)雜度分析


3 仿真結(jié)果
通過(guò)仿真,驗(yàn)證并比較了本文所提出的基于部分內(nèi)波束干擾消除的低復(fù)雜度波束成形以及傳統(tǒng)波束成形的性能。
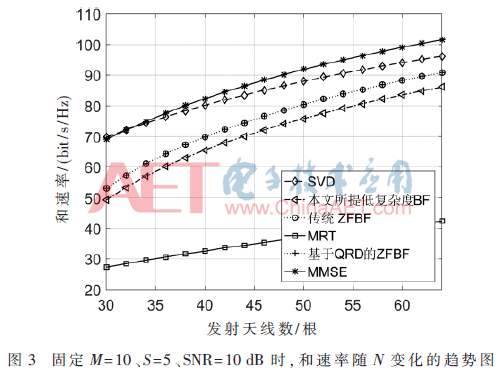
圖2和圖3描繪了當(dāng)10個(gè)用戶信號(hào)以信噪比(SNR)為10 dB進(jìn)行空間復(fù)用時(shí),6種方案的和速率以及浮點(diǎn)計(jì)算數(shù)隨發(fā)射天線數(shù)變化的曲線,其中本文提出的基于部分內(nèi)波束干擾消除的低復(fù)雜度BF算法的干擾消除數(shù)S為5。
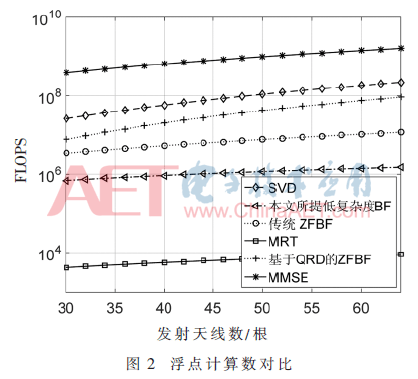
從圖2中可以看出,本文所提方案的浮點(diǎn)計(jì)算數(shù)要顯著低于MMSE、SVD、ZFBF等較優(yōu)的傳統(tǒng)波束成形算法,且其曲線隨著發(fā)射天線數(shù)的增加更加趨于平緩;還可以看出基于QRD的ZFBF由于矩陣求逆運(yùn)算和額外的組合運(yùn)算,其浮點(diǎn)計(jì)算數(shù)要高于傳統(tǒng)ZFBF。
由圖3可見(jiàn),本文所提方案的和速率性能接近于MMSE、SVD、ZFBF等較優(yōu)的波束成形算法,遠(yuǎn)高于MRT波束成形算法,且隨著基站天線數(shù)的增大,所提方案和速率逼近傳統(tǒng)ZFBF的和速率,可以實(shí)現(xiàn)ZFBF近90%的和速率,而只需要ZFBF的12%~19%的計(jì)算復(fù)雜度。
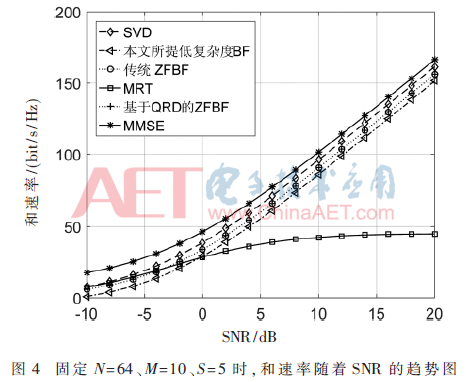
圖4描繪了本文所提方案以及5種傳統(tǒng)波束成形算法的和速率性能隨信噪比變化曲線比較圖(N=64、M=10、S=5)。由圖可知,本文所提低復(fù)雜度BF的和速率接近于MMSE、SVD、ZFBF等較優(yōu)波束成形算法,遠(yuǎn)大于MRT,并且隨著信噪比的增大,和速率性能逼近ZFBF。
4 總結(jié)
大規(guī)模MIMO系統(tǒng)中,傳統(tǒng)的波束成形算法,如MMSE、SVD、ZFBF等雖能提供較優(yōu)的和速率性能,但是復(fù)雜度較高的高維矩陣求逆使其在現(xiàn)實(shí)實(shí)施中比較困難。MRT算法雖然復(fù)雜度最低,最易于實(shí)際應(yīng)用,但是其和速率性能也是最差的。本文提出一種基于部分內(nèi)波束干擾消除的低復(fù)雜度BF算法,首先在MRT場(chǎng)景下確立波束成形矩陣,再通過(guò)內(nèi)波束干擾消除算法的一系列矢量運(yùn)算生成新的波束成形矩陣,以此避開(kāi)復(fù)雜度高的矩陣求逆操作。本文所提方案的計(jì)算復(fù)雜度較ZFBF得到了顯著降低,同時(shí)其和速率性能接近于ZFBF的和速率,遠(yuǎn)大于MRT的和速率,所以此方案更適用于實(shí)際的應(yīng)用。
參考文獻(xiàn)
[1] LARSSON E G,EDFORS O,TUFVESSON F,et al.Massive MIMO for next generation wireless systems[J].IEEE Communications Magazine,2014,52(2):186-195.
[2] MARZETTA T L.Noncooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communications,2010,9(11):3590-3600.
[3] RUSEK F,PERSSON D,LAU B K,et al.Scaling up MIMO:Opportunities and challenges with very large arrays[J].IEEE Signal Processing Magazine,2013,30(1):40-60.
[4] NGO H Q,LARSSON E G,MARZETTA T L.Energy and spectral efficiency of very large multiuser MIMO systems[J].IEEE Transactions on Communications,2013,61(4):1436-1449.
[5] SHEN Z,CHEN R,ANDREWS J G,et al.Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization[J].IEEE Transactions on Signal Processing,2006,54(9):3658-3663.
[6] CHRISTENSEN S S,AGARWAL R,DE CARVALHO E,et al.Weighted sum-rate maximization using weighted MMSE for MIMO-BC beamforming design[J].IEEE Transactions on Wireless Communications,2008,7(12):4792-4799.
[7] SUN F,DE CARVALHO E.A leakage-based MMSE beamforming design for a MIMO interference channel[J].IEEE Signal Processing Letters,2012,19(6):368-371.
[8] ZHAN C Z,CHEN Y L,WU A Y.Iterative superlinear-convergence SVD beamforming algorithm and VLSI architecture for MIMO-OFDM systems[J].IEEE Transactions on Signal Processing,2012,60(6):3264-3277.
[9] SUDHIR A C,RAO B P.Implementation of wireless model for SVD based beam forming in MIMO systems[C].Devices,Circuits and Systems(ICDCS),2014 2nd International Conference on.IEEE,2014:1-6.
[10] PARFAIT T,KUANG Y,JERRY K.Performance analysis and comparison of ZF and MRT based downlink massive MIMOsystems[C].Ubiquitous and Future Networks (ICUFN),2014 Sixth International Conf on.IEEE,2014:383-388.
[11] CORVAJA R,ARMADA A G.Phase noise degradation in massive MIMO downlink with zero-forcing and maximum ratio transmission precoding[J].IEEE Transactions on Vehicular Technology,2016,65(10):8052-8059.
[12] LIU D,MA W,SHAO S,et al.Performance analysis of TDD reciprocity calibration for Massive MU-MIMO systems with ZF beamforming[J].IEEE Communications Letters,2016,20(1):113-116.
[13] CAIRE G,SHAMAI S.On the achievable throughput of a multiantenna Gaussian broadcast channel[J].IEEE Transactions on Information Theory,2003,49(7):1691-1706.
作者信息:
周應(yīng)超,黃 瓊,申 濱
(重慶郵電大學(xué) 移動(dòng)通信技術(shù)重點(diǎn)實(shí)驗(yàn)室,重慶400065)

