0 引言

    對于火星著陸任務(wù)，火星探測器在EDL(Entry,，Descent,，Landing)階段與地球通信非常具有挑戰(zhàn)性,。火星探測器進入火星大氣后會劇烈減速,，這種加速度和抖動使發(fā)送的X波段信號(8.4 GHz)產(chǎn)生嚴重的多普勒動態(tài),。1999年，美國發(fā)射的“火星極地探測器”(Mars Polar Lander,，MPL)由于經(jīng)費限制,，沒有設(shè)計EDL過程中的通信系統(tǒng)，任務(wù)失敗后難以找到失敗的根本原因^[1],。此后，美國進行的火星探測軟著陸任務(wù)在EDL過程中都采用了MFSK通信方式,。因此,，研究火星探測器在EDL過程中的通信體制能為我國火星探測的實施提供借鑒，具有重要意義,。

    火星探測器EDL過程中,，利用直接對地通信鏈路發(fā)送一種類似于旗語的MFSK信號，通過數(shù)據(jù)音與載波之間的頻率間隔來傳遞信息,。由于通信距離極遠,，且多普勒動態(tài)非常大，接收信號載噪比通常在24 dB-Hz以下^[2],，進行這種極低信噪比,、高動態(tài)信號檢測的方法有：(1)最大似然（ML）準則估計算法：傳統(tǒng)的最大似然估計算法是基于多維搜索的非線性優(yōu)化問題，運算復雜度較高,，很難進行實際應(yīng)用,。文獻[3]針對高動態(tài)微弱信號提出了基于最大似然法的頻率估計方法，該算法是最基本的最大似然估計算法,，運算量龐大,；文獻[4]提出了基于相位加權(quán)求和、1階2階相位差的參數(shù)估計算法,，簡化了傳統(tǒng)的最大似然估計算法,；文獻[5]提出了一種離散的高階相位函數(shù)法，可用于高階多普勒動態(tài)估計,，但該方法只適用于中高信噪比時載波捕獲,；文獻[6]提出了一種載波恢復增強的最大似然多普勒頻率偏移算法，該算法通過增加數(shù)據(jù)音,、數(shù)據(jù)音相位兩個維度的搜索,，將信號檢測門限降低了3 dB，但是這種方法的運算量會擴大2 000倍,，不可能進行信號實時檢測,；(2)含F(xiàn)FT處理的最大似然檢測算法：文獻[7-8]提出了時域匹配平均周期圖算法(Time-Domain Matching-Average Periodogram algorithm，TDMAP)，這種算法減弱了多普勒變化率匹配精度要求,，運算復雜度降低,，適用于載波捕獲。但當動態(tài)范圍擴大時,，匹配支路也成比例增加,，運算復雜度擴大，從而給火星探測信號的載波實時捕獲帶來困難,。文獻[9-10]針對傳統(tǒng)的時域匹配平均周期圖算法計算復雜度高的問題,，提出了一種改進的帶有補零的頻域移位平均周期圖算法。該算法與原算法相比,，其計算復雜度降低倍數(shù)為匹配支路數(shù)與補零倍數(shù)之比,，捕獲性能幾乎不損失。文獻[11-12]對高動態(tài)微弱信號完成頻率捕獲后提出了一種自適應(yīng)的信號跟蹤方法,。

    以上研究成果主要用于對極低信噪比,、高動態(tài)信號進行載波捕獲/跟蹤、信息檢測,，沒有從信號體制上分析研究MFSK信號不同的調(diào)制指數(shù)對信號檢測性能的影響,，沒有研究為什么火星科學實驗室(MSL)將MFSK數(shù)據(jù)音之間的頻率間隔設(shè)為76 Hz，不同的頻率間隔對信號檢測性能是否有影響,。另外,，多普勒頻率變化率的大小對信號檢測性能的影響也未進行定量分析。

    本文分析了MER,、Phoenix,、MSL在火星EDL過程中直接對地通信使用的MFSK信號及文獻[7-8]中用于MFSK信號檢測的時域匹配平均周期圖算法，通過仿真火星科學實驗室EDL過程中的多普勒動態(tài),，研究了MFSK調(diào)制指數(shù),、數(shù)據(jù)音頻率間隔以及捕獲/跟蹤階段多普勒頻率變化率的大小對信息解算性能的影響，并根據(jù)研究成果提出以下建議：將數(shù)據(jù)音頻率間隔設(shè)為80 Hz,，當載噪比噪比低于17 dB-Hz時,，調(diào)制指數(shù)應(yīng)設(shè)為45°，否則應(yīng)設(shè)為48°,，多普勒頻率變化率的大小對信息檢測性能影響較大,，當多普勒頻率變化率絕對值高于500 Hz/s時，信號檢測門限會增加3 dB,。

1 火星EDL過程中MFSK信號

    火星探測器EDL過程中直接對地通信采用一種特殊的多子載波調(diào)制體制^[2],，其信號是MFSK側(cè)音信號，信號模型為：

    MFSK信號的頻譜中存在著數(shù)據(jù)音的諧波分量,，這些諧波分量是無用的,，然而會占用一部分信號能量,。進一步將信號中的數(shù)據(jù)音的功率細分為兩部分：基波所占的能量P_dsc、多次諧波所占的能量P_dh,。通過計算可知,，在傳輸?shù)目偰芰恐校敠ぁ?8°時,，傳輸?shù)妮d波能量P_T·cos²Δ正好等于數(shù)據(jù)音的基波分量所占的能量P_T·sin²Δ·8/π²,。圖1是Δ值為48°時MFSK信號的頻譜圖^[7]。

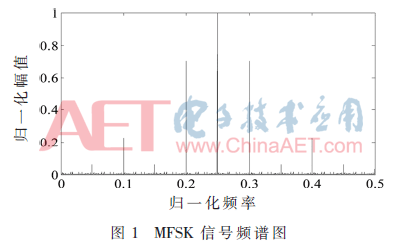
2 火星EDL過程中通信性能分析

2.1 仿真參數(shù)設(shè)置

    根據(jù)文獻[13]可知,，火星探測器在EDL過程中X波段直接對地通信的多普勒偏移范圍(雙向)大約為90 kHz,，正向多普勒頻率大約為50 kHz，多普勒變化率最大為700 Hz/s～1 200 Hz/s,，多普勒頻率的二階導數(shù)大約為-25 Hz/s²～40 Hz/s²,；共發(fā)出256個不同的數(shù)據(jù)音，每隔10 s切換發(fā)射的數(shù)據(jù)音,。設(shè)定為基帶仿真，仿真的采樣率設(shè)為F_s=100 kHz,，信號參數(shù)設(shè)置如表1所示,。

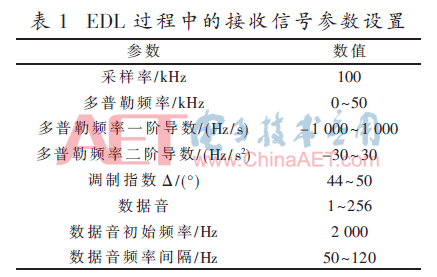
    每次仿真1 000 s，每隔10 s發(fā)送一個[1,，256]之間的隨機數(shù)據(jù)音,，信號在EDL過程中的多普勒頻率、多普勒頻率變化率,、多普勒二階導數(shù)等參數(shù),，參照文獻[7-8]中MER和MSL的動態(tài)范圍進行設(shè)置。假設(shè)初始多普勒頻率為20 kHz,、初始多普勒頻率變化率為-250 Hz/s,，仿真動態(tài)范圍精確到多普勒二階導數(shù)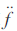，仿真產(chǎn)生火星探測器EDL過程中接收到的信號,。

    EDL過程中的多普勒動態(tài)包絡(luò)和數(shù)據(jù)音的設(shè)置如圖2所示,。其中150 s～300 s之間的高動態(tài)是火星探測器進入火星大氣層時，劇烈的大氣摩擦所致,，圖2(b),、(c)中500 s左右的尖峰是降落傘打開時火星探測器產(chǎn)生的劇烈抖動。

    根據(jù)火星探測器在EDL過程中的不同階段,，利用文獻[7-8]中介紹的TDMAP算法進行載波頻率的捕獲,、跟蹤，以及信息的解算,。利用TDMAP算法進行信號檢測時,，部分參數(shù)如表2所示,。

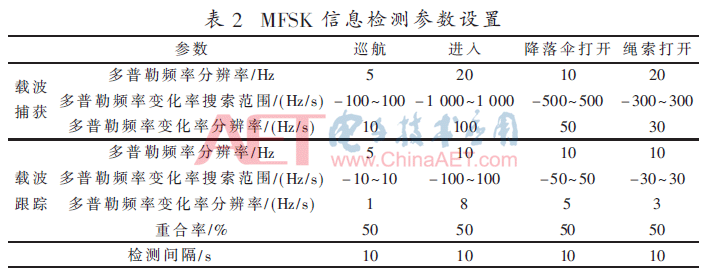
2.2 數(shù)據(jù)音頻率間隔對信息檢測性能的影響

    數(shù)據(jù)音之間的頻率間隔主要受到載波捕獲/跟蹤階段多普勒頻率、多普勒頻率變化率分辨率和信號帶寬的影響,，理論上數(shù)據(jù)音的頻率間隔只要大于頻率搜索精度就能完成信息檢測,。

    將調(diào)制指數(shù)設(shè)為48°，考慮到信息檢測過程中載波捕獲/跟蹤的頻率分辨率以及實際信號帶寬,，數(shù)據(jù)音頻率間隔分別設(shè)為50 Hz,、60 Hz、70 Hz,、80 Hz,、90 Hz、100 Hz,、110 Hz,、120 Hz。每個數(shù)據(jù)音頻率間隔下重復仿真100次,，得到載噪比為16 dB-Hz～20 dB-Hz時的信息誤檢率,，如圖3所示。

    通過仿真結(jié)果可以看出：不同數(shù)據(jù)音頻率間隔時,，MFSK信息檢測性能幾乎相同,，因此相鄰數(shù)據(jù)音之間的頻率間隔對信息檢測性能的影響較小。當數(shù)據(jù)音頻率間隔為80 Hz時,，它的信息檢測門限為18.75 dB-Hz,，較其他的檢測門限稍低。綜合考慮信號帶寬,，建議相鄰數(shù)據(jù)音的頻率間隔設(shè)為80 Hz,。

2.3 調(diào)制指數(shù)對信息檢測性能的影響

    由式(4)、(5)可知,，減小調(diào)制指數(shù),，載波將占有更多功率，有利于載波的頻率捕獲/跟蹤,，但是數(shù)據(jù)音占有的功率相應(yīng)減少,，不利于數(shù)據(jù)音的解算。因此當信號多普勒動態(tài)較大,、信噪比較低時,，合理地分配載波與數(shù)據(jù)音的基波分量所占有的功率有利于提高信息的解算性能。

    將數(shù)據(jù)音頻率間隔設(shè)為80 Hz,，調(diào)制指數(shù)分別為44°,、45°、46°,、47°,、48°,、49°、50°,，每個調(diào)制指數(shù)下重復仿真100次,，得到載噪比分別為16 dB-Hz～20 dB-Hz時的數(shù)據(jù)音誤檢率。圖4為調(diào)制指數(shù)分別為45°和48°時MFSK信息檢測結(jié)果,。

    從圖4可以看出：當載噪比為16.25 dB-Hz和16.5 dB-Hz,，調(diào)制指數(shù)為48°時誤檢率較高的數(shù)據(jù)音比45°時多了第3、11,、12,、45、61,、66,、85、86,、88個數(shù)據(jù)音,；當載噪比為19.5 dB-Hz和19.75 dB-Hz時，調(diào)制指數(shù)為45°仍會在第21,、30個數(shù)據(jù)音發(fā)生誤檢,，而調(diào)制指數(shù)為48°時則沒有發(fā)生誤檢。綜合分析可得,，載噪比低于17 dB-Hz時，把調(diào)制指數(shù)設(shè)為45°更利于信息檢測,，當載噪比高于17 dB-Hz時,，把調(diào)制指數(shù)設(shè)為48°更利于信息檢測。

2.4 多普勒頻率變化率對信息檢測性能的影響

    根據(jù)火星探測器EDL過程中發(fā)射信號多普勒頻率變化率絕對值的大小,，將多普勒動態(tài)劃分為3個級別,，其中第一、二,、三級分別為多普勒頻率變化率的絕對值為0～100 Hz/s,、100 Hz/s～500 Hz/s、500 Hz/s～1 000 Hz/s之間,。將調(diào)制指數(shù)設(shè)為48°,，數(shù)據(jù)音頻率間隔設(shè)為80 Hz，載噪比分別為11 dB-Hz～20 dB-Hz,，間隔為0.25 dB,，其余仿真參數(shù)如表1和表2所示，重復仿真100次,，得到不同載噪比下3種多普勒動態(tài)時的信息檢測結(jié)果,，如圖5所示,。

    從圖5可以看出，多普勒頻率變化率絕對值在0～100 Hz/s,、100 Hz/s～500 Hz/s,、500 Hz/s～1 000 Hz/s時的信息檢測門限大約為15 dB-Hz、16.25 dB-Hz,、19.5 dB-Hz,，因此多普勒頻率變化率的動態(tài)范圍對信息檢測性能影響較大。

3 結(jié)束語

    本文針對火星探測器在EDL過程中直接對地通信鏈路采用的MFSK通信方式,，研究了MFSK調(diào)制指數(shù),、數(shù)據(jù)音頻率間隔以及載波捕獲/跟蹤階段多普勒頻率變化率的大小對信息解算性能的影響。根據(jù)研究結(jié)果,，得出以下結(jié)論：

    (1)相鄰數(shù)據(jù)音之間的頻率間隔對檢測性能的影響較小,，綜合考慮信號帶寬，建議相鄰數(shù)據(jù)音的頻率間隔設(shè)為80 Hz,。

    (2)合理分配載波與數(shù)據(jù)音所占能量,，有利于提高信息檢測性能，當載噪比低于17 dB-Hz時,，將調(diào)制指數(shù)設(shè)為45°,，否則將調(diào)制指數(shù)設(shè)為48°，更有利于信息檢測,。

    (3)多普勒頻率的大小對信息的正確檢測沒有影響,，多普勒頻率變化率的大小對信息的檢測檢測性能有較大影響；多普勒頻率變化率在500 Hz/s以上時數(shù)據(jù)音的檢測門限要提高3 dB,。

由于載波捕獲/跟蹤時只考慮了多普勒頻率,、多普勒頻率變化率，沒有考慮多普勒頻率的二階及高階導數(shù),，如何定量分析多普勒頻率的二階導數(shù)對信息檢測性能的影響是下一步的研究方向,。

參考文獻

[1] KORNLELD R P，UARCIA M D,，CRAIG I E,，et al.Entry，descent,，and landing communications for 2007 Phoenix Mars Lander[J].Journal of Spacecraft and Rockets,，2008，45(3)：534-547.

[2] BRIAN C S,，MELISSA S,，PETER I.Telecommunications performance during entry，descent,，and landing of the mars science laboratory[J].Journal of Spacecraft and Rockets,，2014,，51(4)：1237-1250.

[3] VILNROTTER V A，HINEDI S,，KUMAR R.Frequency estimation techniques for high dynamic trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,，1989，25(4)：559-577.

[4] LI Y,，F(xiàn)U H,，KAM P Y.Improved，approximate,，time-do-mam ML estimators of chirp signal parameters and their performance analysis[J].IEEE Transactions on Signal Processing,，2009，57(4)：1260-1272.

[5] FARQUHARSON M,，O′SHEA P,，LEDWICH G.A computational1y efficient technique for estimating the parameters of polynomial-phase signals from noisy observations[J].IEEE Transactions on Signal Processing，2000,，53(8)：3337-3342.

[6] CATTIVELLI F S,，ESTABROOK P，SATORIUS E H,，et al.Carrier recovery ehancement for maximum-likelihood Doppler shift estimation in mars exploration missions[J].IEEE Journal of Selected Topics in Signal Processing,，2008，2(5)：658-669.

[7] SATORIUS E,，ESTABROOK P,，WILSON J，et al.Direct-to-earth communications and signal processing for mars exploration rover entry,，descent,，and landing[R].Reston：The Interplanetary Network Progress，2003：42-153.

[8] SORIANO M,，F(xiàn)INLEY S，F(xiàn)ORT D,，et al.Direct-to-earth communications with mars science laboratory during entry,，descent，and landing[C].IEEE Aerospace Conference,，Big Sky,，MT：AERO，2013：1-14.

[9] 甘浩,，張曉林,，馬月紅，等.一種改進的深空高動態(tài)微弱信號頻率捕獲算法[J].遙測遙控,，2015,，36(4)：6-11.

[10] 段瑞楓,，劉榮科，周游,，等.一種低復雜度的極低信噪比高動態(tài)信號載波粗捕獲算法[J].航空學報,，2013，34(3)：662-669.

[11] LOPES C G,，SATORIUS E,，ESTABROOK P，et al.Efficient adaptive carrier tracking for mars to earth communications during entry,，descent and landing[C].IEEE/SP 14th  Workshop Signal Processing.Madison,，WI：IEEE SSP，2007,，1：517-521.

[12] LOPES C G,，SATORIUS E，SAYED A H.Adaptive carrier tracking for mars to earth communications during entry,，descent and landing[C].Proc.of 40th Asiomar Conference on Signal and Computers.Pacific Grove,，CA：IEEE ACSSC，2006：1042-1046.

[13] KORNFELD R P,，PRAKASH R,，DEVEREAUX A S，et al.Verification and validation of the mars science laboratory/curiosity rover entry,，descent,，and landing system[J].Journal of Spacecraft and Rockets，2014,，51(4)：1251-1269.

作者信息:

張?zhí)靹?,，張曉林1，李  贊2

（1.北京航空航天大學 電子信息工程學院,，北京100191,；2.北京跟蹤與通信技術(shù)研究所，北京100094）