0 引言

    現(xiàn)實中的社會經(jīng)濟網(wǎng)絡與各種電力、通信、水電等基礎(chǔ)設(shè)施網(wǎng)絡存在邏輯和功能上的依賴，一個網(wǎng)絡的運行依賴于另一個或幾個網(wǎng)絡的運行，比如電力網(wǎng)絡正常運行為通信網(wǎng)絡提供電力保障，通信網(wǎng)絡正常運行又給電力網(wǎng)絡提供調(diào)控信息，彼此形成更復雜的電力-通信網(wǎng)絡。這種由若干網(wǎng)絡彼此依賴而耦合成的網(wǎng)絡稱為“相依網(wǎng)絡”。

    相依網(wǎng)絡的正常運行至關(guān)重要，相應的故障研究工作起源于文獻[1]，BULDYREV S V在文獻[1]中研究了一對一互連的全相依網(wǎng)絡模型，得出相依網(wǎng)絡的故障滲流過程為一階形式，即網(wǎng)絡節(jié)點比例移除達到一定閾值，網(wǎng)絡完整性會急劇下降，這一結(jié)論有別于單一或孤立網(wǎng)絡，單一或孤立網(wǎng)絡移除節(jié)點時的表現(xiàn)形式是逐步下降的二階形式。文獻[2]對相依網(wǎng)絡采用負載局部分配原則的容量-負載模型，分析子網(wǎng)絡間的耦合強度、子網(wǎng)絡類型和耦合邊的故障影響。文獻[3]研究不同攻擊策略對相依網(wǎng)絡的影響，發(fā)現(xiàn)同時考慮不同子網(wǎng)節(jié)點度的攻擊策略比考慮單一子網(wǎng)的攻擊策略更有效、破壞更嚴重。文獻[4]介紹相依網(wǎng)絡的來龍去脈，并以經(jīng)濟網(wǎng)絡的相依網(wǎng)絡為例，得出不同經(jīng)濟因素的排名，表明中國經(jīng)濟增長趨勢強勁。文獻[5]在相依網(wǎng)絡的故障中綜合考慮相依邊的依賴關(guān)系、負載作用，提出一種相依網(wǎng)絡模型，同時還提出一種主動的、但存在微弱擾動的故障恢復策略。文獻[6]提出一種節(jié)點外部度和內(nèi)部度可調(diào)關(guān)系的相依網(wǎng)絡負載-容量模型，以研究外部度和內(nèi)部度等因素對級聯(lián)故障的影響。文獻[7]構(gòu)建雙層相依控制網(wǎng)絡模型，發(fā)現(xiàn)子網(wǎng)的平均度越大，網(wǎng)絡越魯棒。文獻[8]提出網(wǎng)絡間同地位節(jié)點耦合的相依網(wǎng)絡構(gòu)建方法，將隨機網(wǎng)絡和無標度網(wǎng)絡作為耦合的子網(wǎng)，模擬故障滲流由一階非連續(xù)相變到二階連續(xù)相變的過程。文獻[9]提出一種考慮負載作用的級聯(lián)故障模型和低成本的故障抑制策略。

    上述研究現(xiàn)狀存在幾點不足：(1)負載分配策略采用局部分配策略，而實際中的節(jié)點故障會導致網(wǎng)絡負載發(fā)生全局重分配；(2)評估指標局限于最大連通子圖，故障評估不夠全面。本文基于節(jié)點負載全局重分配策略，對相依邊為邏輯依賴的相依網(wǎng)絡仿真分析，采用（非）最大連通子圖占比、迭代步長和首次迭代中（平均/最大）最短路徑長度等指標對相依網(wǎng)絡進行較全面的評估。

1 相依網(wǎng)絡模型

1.1 相依網(wǎng)絡簡述

    單個或孤立的子網(wǎng)之間通過物理依附、邏輯依賴等方式耦合成相依網(wǎng)絡。連接不同子網(wǎng)節(jié)點的邊稱作相依邊，物理依附是指相依邊兩側(cè)的不同子網(wǎng)節(jié)點存在功能依賴：相依邊一側(cè)節(jié)點故障，另一側(cè)節(jié)點也同樣會故障。邏輯依賴是指相依邊兩側(cè)不同子網(wǎng)節(jié)點存在結(jié)構(gòu)上的邏輯依賴：相依邊一側(cè)節(jié)點故障不一定會導致另一側(cè)節(jié)點故障。

    節(jié)點度指節(jié)點的鄰居節(jié)點數(shù)目，度越大，節(jié)點鄰居節(jié)點越多。不同子網(wǎng)的節(jié)點一對一互連耦合時，存在3種耦合方式：隨機耦合、同配耦合和異配耦合。隨機耦合指一子網(wǎng)中節(jié)點隨機選擇另一子網(wǎng)中節(jié)點連接。同配耦合指一子網(wǎng)中大度節(jié)點與另一子網(wǎng)中大度節(jié)點連接，而小度節(jié)點與另一子網(wǎng)中小度節(jié)點連接。異配耦合指一子網(wǎng)中大度節(jié)點與另一子網(wǎng)中小度節(jié)點連接^[10]。

    子網(wǎng)中參與連邊耦合的節(jié)點占比代表耦合強度，節(jié)點占比越大說明耦合強度越大，若兩個子網(wǎng)的全部節(jié)點參與耦合互連，則稱為全相依網(wǎng)絡，否則稱為部分相依網(wǎng)絡。

1.2 相依網(wǎng)絡模型構(gòu)建過程

    將某個獨立的子網(wǎng)記作子網(wǎng)1，對子網(wǎng)1復制一份副本，記作子網(wǎng)2。按照以下2步構(gòu)建全相依網(wǎng)絡：

    (1)依據(jù)不同節(jié)點度（即節(jié)點的鄰居節(jié)點數(shù)目）排序規(guī)則，對子網(wǎng)1和子網(wǎng)2中節(jié)點排序，見表1。

    (2)按照表1，對子網(wǎng)1和子網(wǎng)2中全部節(jié)點自上而下一對一依次互連。

    通過以上步驟，生成隨機耦合全相依網(wǎng)絡、同配耦合全相依網(wǎng)絡和異配耦合全相依網(wǎng)絡，在不引起歧義的前提下，分別簡稱：隨機網(wǎng)絡、同配網(wǎng)絡和異配網(wǎng)絡。圖1是隨機耦合的全相依網(wǎng)絡的示意圖。

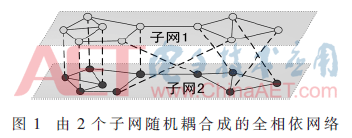
    圖1是由子網(wǎng)1和子網(wǎng)2節(jié)點一對一隨機互連的全相依網(wǎng)絡。實線代表子網(wǎng)內(nèi)的連邊，稱之為“連接邊”，虛線代表子網(wǎng)間的“相依邊”。

2 負載全局重分配的級聯(lián)故障模型

    通信、電力等網(wǎng)絡，其信息等物理量在網(wǎng)絡節(jié)點對之間傳遞，每個節(jié)點有一定初始負載和容量以維持網(wǎng)絡功能。

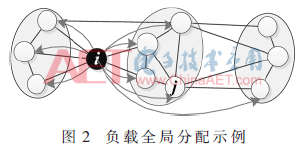
3 相依網(wǎng)絡的性質(zhì)

    仿真所用子網(wǎng)數(shù)據(jù)為電網(wǎng)拓撲IEEE118網(wǎng)絡和新英格蘭高壓電England網(wǎng)絡，分別為118個節(jié)點和120個節(jié)點。依據(jù)前文的相依網(wǎng)絡模型，形成IEEE118隨機網(wǎng)絡、IEEE118同配網(wǎng)絡、IEEE118異配網(wǎng)絡、England隨機網(wǎng)絡、England同配網(wǎng)絡和England異配網(wǎng)絡，拓撲性質(zhì)如表2和表3所示。

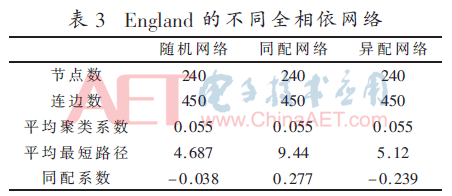
    依表2和表3可知，不同耦合方式相依網(wǎng)絡的平均聚類系數(shù)近似，隨機網(wǎng)絡和異配網(wǎng)絡的平均最短路徑比同配網(wǎng)絡小。同配網(wǎng)絡的同配系數(shù)為正數(shù)，而隨機網(wǎng)絡和異配網(wǎng)絡的同配系數(shù)為負數(shù)，這與相依網(wǎng)絡構(gòu)建原理一致。

4 不同評估指標的仿真分析

    采用MATLAB仿真級聯(lián)故障，初始故障節(jié)點選擇子網(wǎng)1中節(jié)點，相依邊為邏輯依賴。子網(wǎng)2節(jié)點只會由于過載而故障，不會由于相依邊的依賴而故障。采用多個指標評估級聯(lián)故障對相依網(wǎng)絡的影響，仿真結(jié)果為子網(wǎng)1中全部節(jié)點迭代20次的平均值。

4.1 最大連通子圖分析

4.1.1 最大連通子圖占比

    由于相依網(wǎng)絡中不同子網(wǎng)部分節(jié)點之間存在邏輯依賴，所以限定評估指標—最大連通子圖必需同時包含2個子網(wǎng)的節(jié)點，否則說明網(wǎng)絡已完全崩潰。

    最大連通子圖占比表征為故障后剩余節(jié)點中最大連通子圖節(jié)點數(shù)目在節(jié)點總數(shù)中的占比，占比越大，級聯(lián)故障對相依網(wǎng)絡的破壞作用越小，結(jié)果如圖3所示。

    分析可知，容忍系數(shù)β越大，最大連通子圖占比越大，級聯(lián)故障的破壞作用越小。IEEE118和England的隨機網(wǎng)絡和異配網(wǎng)絡在不同β下的級聯(lián)故障結(jié)果類似。在β=0時，同配網(wǎng)絡對應的最大連通子圖占比偏大，級聯(lián)故障破壞最小；而0.1≤β≤0.8時，同配網(wǎng)絡對應的最大連通子圖占比偏小，級聯(lián)故障對同配相依網(wǎng)絡的破壞最大。

4.1.2 非最大連通子圖占比

    在每一迭代步后，通過計算不屬于最大連通子圖的節(jié)點數(shù)目與節(jié)點總數(shù)的比值，結(jié)果如圖4所示。

    總體趨勢而言，β越大，非最大連通子圖占比越小，這是由于β越大，網(wǎng)絡越冗余，級聯(lián)故障對網(wǎng)絡的破壞越小，不屬于最大連通子圖的節(jié)點越少。同時，在β值一定時，隨機網(wǎng)絡和異配網(wǎng)絡的結(jié)果類似，而同配網(wǎng)絡對應的y值明顯大于隨機網(wǎng)絡和異配網(wǎng)絡，即在遭受級聯(lián)故障后，同配網(wǎng)絡受到更大程度的破壞。

4.2 迭代步長分析

    迭代步長描述從初始故障節(jié)點開始，級聯(lián)故障一層一層擴散的現(xiàn)象，代表網(wǎng)絡達到穩(wěn)態(tài)時的故障迭代次數(shù)。迭代步長越大，網(wǎng)絡達到穩(wěn)定時間越晚，級聯(lián)故障的影響越久；步長越小，網(wǎng)絡達到穩(wěn)態(tài)時間越早，級聯(lián)故障的影響越短，結(jié)果如圖5所示。

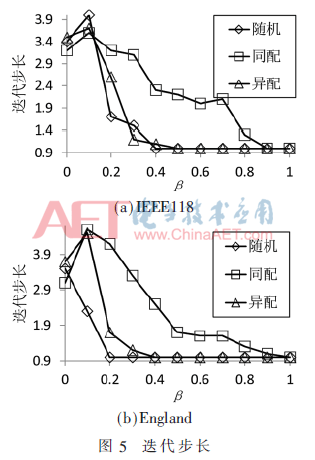
    由圖可知，迭代步長總體趨勢為隨著β變化，先增加至峰值再遞減。β=0.1時，迭代步長達到峰值，β>0.1，迭代步長隨著網(wǎng)絡冗余的增大而減少，且同配網(wǎng)絡的迭代步長下降最為緩慢，網(wǎng)絡達到穩(wěn)定越晚。IEEE118同配網(wǎng)絡在β≤0.1時，達到穩(wěn)定更早。England不同相依網(wǎng)絡在β≥0.1時，迭代步長差異顯著。

4.3 首次迭代步中最短路徑長度分析

4.3.1 首次迭代步中過載節(jié)點的平均最短路徑長度

    初始故障節(jié)點i，定義f(n)為第n個迭代步中過載節(jié)點集合，|f(n)|代表相應的節(jié)點數(shù)目，k∈f(n)，則：

其中，dst(1)為首次故障迭代步中過載節(jié)點的平均最短路徑長度。由于在n≥2時，不同迭代步之間存在多個故障觸發(fā)源，不便于分析，這里取n=1。圖6是相依網(wǎng)絡首次迭代步中過載節(jié)點的平均最短路徑長度。

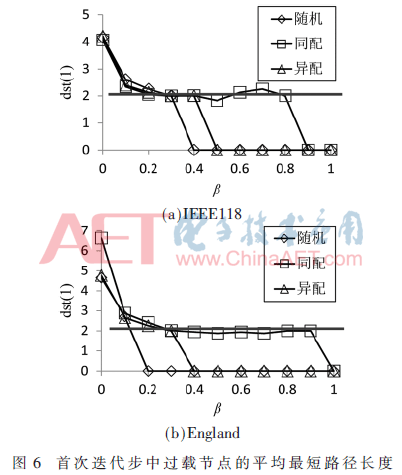
    由圖6可知，β∈(0，0.2)時，β越大，dst(1)越小，說明網(wǎng)絡越冗余，過載節(jié)點越傾向分布在初始故障節(jié)點附近。對比隨機網(wǎng)絡和異配網(wǎng)絡，同配網(wǎng)絡在β≥0.3時，dst(1)略有波動但總體不變，說明網(wǎng)絡冗余超過一定閾值，過載節(jié)點與初始故障節(jié)點具備相對不變距離(≈2)，即故障節(jié)點鄰居節(jié)點的鄰居節(jié)點。隨機網(wǎng)絡和異配網(wǎng)絡的dst(1)在更小的β下達到0，這是因為隨機網(wǎng)絡和異配網(wǎng)絡在此β下已達到穩(wěn)態(tài)。在β=0(即網(wǎng)絡無冗余)時，England同配網(wǎng)絡的過載節(jié)點傾向分布在遠離初始故障節(jié)點處，而IEEE118不同相依網(wǎng)絡則無區(qū)別。

4.3.2 首次迭代步中過載節(jié)點的最大最短路徑長度

    定義f_max(n)為第n次迭代步中，距離初始故障節(jié)點i最遠的過載節(jié)點，則：

其中，dst_max(1)代表首次迭代步中過載節(jié)點的最大最短路徑長度，結(jié)果如圖7所示。

    從圖7可知，dst_max(1)曲線下降趨勢先快后緩慢。當β=0時，過載節(jié)點非常遠離初始故障節(jié)點；β=0.1時，dst_max(1)明顯小于β=0時值，說明較小的網(wǎng)絡冗余能顯著降低最遠的過載節(jié)點距離；繼續(xù)增大網(wǎng)絡冗余（β≥0.2），則對降低過載節(jié)點最遠距離無顯著作用(≈2、3)。IEEE118和England同配網(wǎng)絡在β∈(0，0.4)下的dstmax(1)值明顯區(qū)別于隨機網(wǎng)絡和異配網(wǎng)絡。

5 結(jié)論

    本文對IEEE118電網(wǎng)和England網(wǎng)絡作為子網(wǎng)進行耦合，依據(jù)不同耦合方式，構(gòu)建3種不同的相依網(wǎng)絡。通過對不同相依網(wǎng)絡仿真級聯(lián)故障，并從最大連通子圖、迭代步長和過載節(jié)點分布對級聯(lián)故障深入分析，發(fā)現(xiàn)同配網(wǎng)絡比異配網(wǎng)絡和隨機網(wǎng)絡更脆弱，級聯(lián)故障對同配網(wǎng)絡的破壞更持久，而隨機網(wǎng)絡和異配網(wǎng)絡具備相似的級聯(lián)故障特性。通過本文研究可知，現(xiàn)實網(wǎng)絡耦合時應避免同配方式耦合，在故障發(fā)生前（后）時，應有針對性地預防（檢修）故障節(jié)點的鄰居節(jié)點的鄰居節(jié)點，避免盲目工作。

參考文獻

[1] BULDYREV S V，PARSHANI R，PAUL G，et al.Catastrophic cascade of failures in interdependent networks[C].APS March Meeting 2010.American Physical Society，2010：1025.

[2] 陳世明，鄒小群，呂輝，等.面向級聯(lián)失效的相依網(wǎng)絡魯棒性研究[J].物理學報，2014，63(2)：428-437.

[3] 劉潤然，賈春曉，章劍林，等.相依網(wǎng)絡在不同攻擊策略下的魯棒性[J].上海理工大學學報，2012(3)：235-239.

[4] HAVLIN S，KENETT D Y.Cascading failures in interdependent economic networks[C].Proceedings of the International Conference on Social Modeling and Simulation，plus Econo-physics Colloquium 2014.Springer International Publishing，2015.

[5] Hong Sheng，Lv Chuan，Zhao Tingdi，et al.Cascading failure analysis and restoration strategy in an interdependent network[J].Journal of Physics A Mathematical General，2016，49(19)：195101.

[6] 彭興釗，姚宏，杜軍，等.負荷作用下相依網(wǎng)絡中的級聯(lián)故障[J].物理學報，2015，64(4)：351-358.

[7] 韓海艷，楊任農(nóng)，李浩亮，等.雙層相依指揮控制網(wǎng)絡級聯(lián)失效研究[J].中南大學學報：自然科學版，2015(12)：4542-4547.

[8] 李穩(wěn)國，鄧曙光，楊冰，等.相互依存網(wǎng)絡間的拓撲構(gòu)建方法[J].計算機工程與應用，2014(11)：85-89.

[9] HONG S，WANG B，MA X，et al.Failure cascade in interdependent network with traffic loads[J].Journal of Physics A Mathematical & Theoretical，2015，48(48)：485101.

[10] 劉漳輝，陳國龍，湯振立，等.加權(quán)復雜網(wǎng)絡相繼故障的節(jié)點動態(tài)模型研究[J].小型微型計算機系統(tǒng)，2013，34(12)：2800-2804.

[11] Lin Guoqiang，Di Zengru，F(xiàn)an Ying.Cascading failures in complex networks with community structure[J].International Journal of Modern Physics C，2014，25(5)：323-337.

作者信息:

王  曦，張新剛

(南陽師范學院 軟件學院，河南 南陽473061)