0 引言

    在無(wú)線接收設(shè)備中低噪聲放大器(LNA)的噪聲性能好壞對(duì)整個(gè)系統(tǒng)設(shè)備有著至關(guān)重要的影響，在生產(chǎn)應(yīng)用中,，CMOS技術(shù)的重點(diǎn)是努力設(shè)計(jì)噪聲非常小的LNA以及噪聲系數(shù)優(yōu)化方法^[1-4],。圍繞著LNA噪聲系數(shù)優(yōu)化方法分析有著大量的研究，文獻(xiàn)[5]深入分析了LNA優(yōu)化技術(shù),，但卻忽略了柵極寄生電阻對(duì)噪聲系數(shù)的影響,。文獻(xiàn)[6-7]指出了一種把噪聲系數(shù)與功率匹配同時(shí)考慮的優(yōu)化技術(shù)，然而卻忽略了柵極電感產(chǎn)生的柵噪聲影響,，且噪聲之間的相關(guān)性表述不確切,。為了保證LNA在恒功耗條件下能夠具有優(yōu)異的噪聲性能，本文引入了柵極寄生阻抗和外加電容,，依據(jù)噪聲理論,，推導(dǎo)出小信號(hào)電路模型的噪聲系數(shù)表達(dá)式，提出了恒功耗條件下的噪聲系數(shù)優(yōu)化方法,。這一方法對(duì)LNA在給定條件下的噪聲優(yōu)化方法設(shè)計(jì)具有明顯的指導(dǎo)意義,。同時(shí)對(duì)提出的噪聲優(yōu)化方法進(jìn)行MATLAB理論仿真，在ADS軟件中對(duì)理論結(jié)果進(jìn)行了仿真驗(yàn)證,。

1 LNA噪聲系數(shù)優(yōu)化方法

    如圖1所示為源極去耦的LNA噪聲小信號(hào)等效電路模型,，其中引入了柵極寄生電阻R_g和外加電容C_ex。柵極電感L_g和柵極寄生電阻R_g在電路品質(zhì)因數(shù)Q_s的提高下，也會(huì)隨之增加,，電路噪聲系數(shù)勢(shì)必會(huì)有增大的趨勢(shì),，而外加電容C_ex的作用在低功耗的約束條件下，使得阻抗和噪聲同時(shí)達(dá)到匹配^[8],。因此,，在功耗恒定時(shí)，為了實(shí)現(xiàn)更好的噪聲系數(shù)優(yōu)化,，柵極寄生電阻及柵極電感的影響在噪聲系數(shù)中應(yīng)體現(xiàn)出來(lái),。

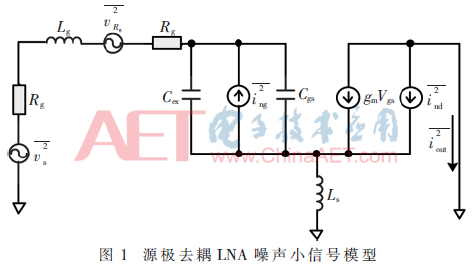
    噪聲系數(shù)的定義為：總的噪聲輸出功率與由輸入噪聲源引起的輸出噪聲功率之比^[9]，即：

    這里引入傳輸函數(shù)Δ(jω)和Γ(jω)分別表示源極噪聲源與它所引起輸出之間的關(guān)系和柵極噪聲源與它所引起輸出之間的關(guān)系,，使用G_m(jω)來(lái)表示晶體管的傳輸增益,。根據(jù)傳輸函數(shù)與柵極源極噪聲互相關(guān)因子，式(1)可以修正為：

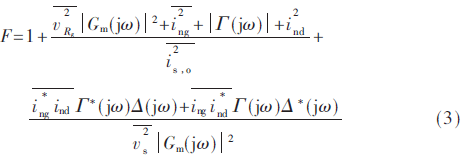
當(dāng)LNA發(fā)生諧振時(shí),，通過它的小信號(hào)噪聲模型可以獲得傳輸函數(shù)的表達(dá)式,。諧振時(shí)有ω₀C_t(L_s+L_g)=1，其中C_t=C_gs+C_ex,。據(jù)此,，可以獲得傳輸函數(shù)表達(dá)式為：

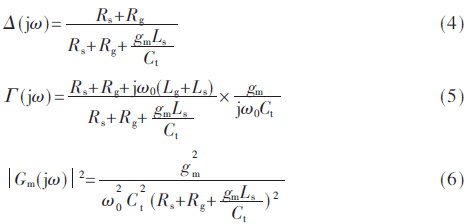
    由式(4)可以看出，由源極噪聲引起的噪聲功率是一個(gè)比例常數(shù),，取決于柵極過載電壓V_GT=V_gs-V_T,，其中V_T是晶體管的閾值電壓。在推導(dǎo)噪聲系數(shù)的過程中,，可以做一些定義：D=R_s+R_g+g_m L_s/C_t,，L_t=L_s+L_g，R=R_g+R_s和Q_s=ω₀ L_t/R,，使得式(4),、式(5)、式（6）書寫簡(jiǎn)便,，即：

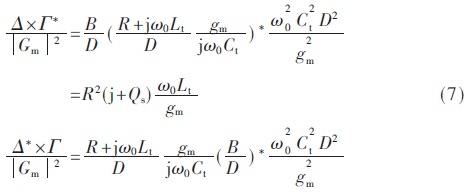
    由于晶體管的兩個(gè)噪聲源都是相關(guān)的,，據(jù)相關(guān)系數(shù)概念，可由式(2)得到：

    因?yàn)樵肼曤妷汗β逝c電流功率都有一個(gè)與之相關(guān)的噪聲電阻,，因此上式可以修正為：

    由于考慮到柵極寄生電阻和外加電容對(duì)噪聲系數(shù)的影響以及晶體管品質(zhì)因數(shù)Q_s與功耗之間的關(guān)系,，據(jù)此可以推導(dǎo)出噪聲系數(shù)的最終表達(dá)式為：

2 結(jié)果及分析

    以圖1作為研究的基本拓?fù)浣Y(jié)構(gòu)，采用ADS軟件以及MATLAB作為仿真設(shè)計(jì)平臺(tái),。其噪聲小信號(hào)模型相關(guān)參數(shù)為：頻率：f=2.5 GHz,，直流電壓：V_dd=1.8 V，速度飽和電壓強(qiáng)度：E_sat=4.7×10⁶ V/m,，電子飽和速率：v_sat=8.43×10⁴ m/s,，柵極方塊多晶硅電阻值：R_sq=10 Ω/sq,，柵值寬度：W_f=2.5 μm，晶體管有效溝道長(zhǎng)度：L=0.16 μm,， 柵源電容：C_gs≤1 pF,，相關(guān)工藝參數(shù)：γ=2/3,、δ=4/3,、c=j0.395，源極電感：L_S≤2 nH,，柵極總電容C_t≤3 pF,，直流功耗：P_D=50 mW，柵極螺旋電感品質(zhì)因素：Q_ind=35,。

    圖2為恒定功耗條件下噪聲系數(shù)隨電路輸入品質(zhì)因數(shù)變化的關(guān)系,。由圖可知，考慮柵極寄生阻抗時(shí),，相比未計(jì)算柵極寄生阻抗時(shí)的噪聲系數(shù)有一定的下降,，這是因?yàn)橥饧与娙莺蜄艠O寄生電阻，平衡了晶體管自身的噪聲與柵極阻抗的噪聲,，同時(shí)外加電容使得源極電感值變小,，從而降低了噪聲系數(shù)，實(shí)現(xiàn)噪聲和阻抗同時(shí)匹配,。

    圖3是Qs=3.3時(shí)仿真結(jié)果,。從圖中可以看出，當(dāng)頻率為2.5 GHz時(shí),，LNA輸入端的反射損耗S11為-32.718 dB,，而反射損耗在-10 dB以下是工程設(shè)計(jì)中的普遍要求。正向傳輸增益為14.167 dB,。為驗(yàn)證當(dāng)Q_s=3.3時(shí)LNA噪聲系數(shù)取得最小值,，對(duì)Q_s在3.3附近取值，利用ADS仿真電路進(jìn)行仿真驗(yàn)證,，得到仿真驗(yàn)證數(shù)據(jù)如圖4所示,。

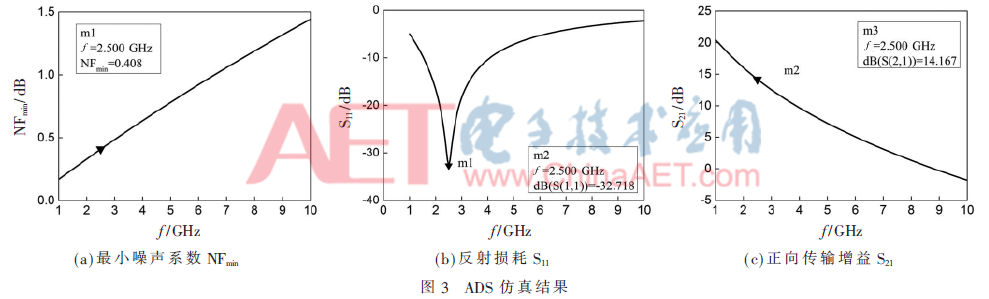
    圖4為不同Q_s值條件下噪聲系數(shù)隨頻率變化的關(guān)系。從圖中可以看出,，Q_s不同,，噪聲系數(shù)不同，即同一頻率基礎(chǔ)下Q_s增加,，最小噪聲系數(shù)也相應(yīng)地增加,，具有偏置依賴性；同一Q_s偏置下,，隨頻率的增加成線性比例增加,，具有頻率依賴性,。同時(shí)也驗(yàn)證了提出的恒功耗條件下噪聲系數(shù)優(yōu)化表達(dá)式的理論結(jié)果的正確性。

3 結(jié)論

    本文基于LNA小信號(hào)噪聲模型,，依據(jù)噪聲理論基礎(chǔ),，推導(dǎo)出此小信號(hào)電路的噪聲系數(shù)表達(dá)式，考慮了恒功耗條件下柵極寄生電阻和柵極電感阻抗以及外加電容對(duì)噪聲系數(shù)的影響,，提出恒功耗條件下的噪聲系數(shù)優(yōu)化方法,。同時(shí)ADS仿真結(jié)果對(duì)理論結(jié)果進(jìn)行了很好地驗(yàn)證，證明了其正確性,。這一方法對(duì)LNA噪聲系數(shù)優(yōu)化設(shè)計(jì)具有指導(dǎo)意義,。

參考文獻(xiàn)

[1] LI J，HASAN S M R.Design and performance analysis of a 866-MHz low-power optimized CMOS LNA for UHF RFID[J].IEEE Transactions on Industrial Electronics,，2013,，60(5)：1840-1849.

[2] LAI M T，TSAO H W.Ultra-Low-Power cascaded CMOS LNA with positive feedback and bias optimization[J].IEEE Transactions on Microwave Theory & Techniques,，2013,，61(5)：1934-1945.

[3] 洪敏，張瑛,，于映,，等.一種低功耗CMOS LNA優(yōu)化設(shè)計(jì)方法[J].南京郵電大學(xué)學(xué)報(bào)：自然科學(xué)版，2015,，35(1)：114-118.

[4] EVARISTE W T,，ADOLPHE M I，DANIEL T,，et al.Noise optimization of readout front ends in CMOS technology with PS circuit[J].Asian Journal of Applied Sciences,，2015，2(5)：752-761.

[5] SHAEFFER D K,，LEE T H.A 1.5-V,，1.5-GHz CMOS low noise amplifier[J].IEEE Journal of solid-state circuits，1997,，32(5)：745-759.

[6] NGUYEN T K,，KIM C H，IHM G J,，et al.CMOS low noise amplifier design optimization technique[C].Circuits and Systems,，2004.Mwscas '04.the 2004，Midwest Symposium on.2004：I-185-8.

[7] GOO J S,，AHN H T,，LADWIG D J，et al.A noise optimization technique for integrated low-noise amplifiers[J].IEEE Journal of Solid-State Circuits,，2002,，37(8)：994-1002.

[8] DENG Z,，NIKNEJAD A M.On the noise optimization of CMOS common-source Low-Noise amplifiers[J].Circuits & Systems I Regular Papers IEEE Transactions on，2011,，58(4)：654-667.

[9] KIM T S,，KIM B S.Post-linearization of cascode CMOS low noise amplifier using folded PMOS IMD sinker[J].IEEE Microwave & Wireless Components Letters，2006,，16(4)：182-184.

[10] 劉鳳,，王軍.CMOS低噪聲放大器的噪聲系數(shù)優(yōu)化[J].通信技術(shù)，2011,，43(10)：121-125.

作者信息:

王丹丹,，王  軍,，王  林

（西南科技大學(xué) 信息工程學(xué)院,，四川 綿陽(yáng)621010）