0 引言

    核磁共振圖像(Magnetic Resonance Image,，MRI)具有無輻射、高分辨率,、多平面成像等優(yōu)點,，廣泛應用于臨床診斷。然而,，緩慢的掃描速度會導致運動偽影的產(chǎn)生,，致使圖像變得模糊和失真，因此研究如何在保證高質量圖像的情況下提高成像速度具有重要的理論和實際應用價值,。壓縮感知(Compressive Sensing,，CS)理論是DONOHO D L、CAND?魬S E J和TAO T等^[1-3]在2006年提出的一種全新的信號采樣和處理理論,。CS理論提供了一個利用少量測量數(shù)據(jù)實現(xiàn)稀疏信號重建的框架,，極大地減少傅里葉變換域的采樣數(shù)據(jù),，縮短掃描時間，提高成像速度,。

    在MRI領域,，CS理論得到極大的認可。LUSTIG M等^[4]利用MRI在小波域的稀疏性和空間域的變分約束,，將CS理論成功應用于心臟成像,、腦成像、快速三維血管造影等,，并取得良好的重建效果,。在Lusting等人的研究基礎上，DABOV K等^[5]在對局部相似性研究的基礎上,，提出一種新的塊匹配重建算法,。AK?覶AKAYA M等^[6]利用塊匹配的重建算法對中心采樣的心臟圖像進行重建，實現(xiàn)了在4倍采樣的MRI的精確重建,。RAVISHANKAR S等^[7]利用K-SVD思想,，提出一種基于自適應字典學習的MRI重建算法,，重建效果得到進一步提高,。RAJWADE A和LINGALA S G等^[8，9]提出的具有盲字典學習的高光譜成像和動態(tài)MRI算法自適應學習字典,獲得了良好的重構性能,。

    字典學習^[10]可以有效表征圖像的特征信息,，全變分(Total Variation,，TV)正則項^[11]可以保持圖像邊緣信息。然而,，在字典學習過程中稀疏編碼會產(chǎn)生混亂信息熵,，影響字典學習效率，TV單向梯度處理平滑區(qū)域會產(chǎn)生階梯效應,。針對以上問題,，本文引入熵約束和加權的TV正則項，充分利用圖像的先驗信息,，構建圖像重構模型,。

1 壓縮感知基本理論

    基于稀疏表示理論，CS理論將信號采樣和壓縮合并進行,，通過非自適應線性投影有效獲取信號的特征信息,，并利用求解最優(yōu)化問題高概率精確重構原信號，緩解了數(shù)據(jù)的采集,、存儲,、傳輸和分析的壓力。一般地,，對于原始信號為x∈C^N,，給定測量值y=Φx∈C^M,，其中Φ∈C^M×N(M<N)是非滿秩測量矩陣，存在無窮多個可行解x,，若Φ滿足約束等距條件,，則可確保重構解唯一。信號重構過程轉換為最小化L₀范數(shù)模型,，即：

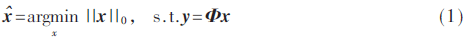
其中||·||₀是零范數(shù),，表示x中非零元素的個數(shù),。求解式(1)不僅是一個NP難問題,，而且極易受到噪聲的影響。針對此問題,，研究者采用凸的L₁范數(shù)代替非凸的L₀范數(shù),，即：

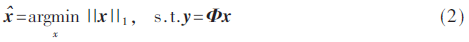
    選擇一個合適的拉格朗日乘子λ，式(2)可轉化為無約束優(yōu)化問題：

    采用Bregman算法,、對偶算法以及交替迭代乘子法等算法均可有效求解式(3),。最近研究表明，圖像信息中包含了大量的自相關結構,，具有高度結構化稀疏性以及低秩特性,，利用這種非局部相似特性構建的低秩結構化稀疏模型^[12]顯示出更為優(yōu)異的圖像重構效果。

2 圖像重構模型的提出

    由于字典學習過程中稀疏系數(shù)索引會產(chǎn)生較高的信息熵,，影響原子學習效率,。而單一的TV正則項又會對圖像邊緣紋理過平滑，產(chǎn)生階梯效應,。為此,，基于熵約束和加權TV正則項提出一種新的圖像重構模型，如下所示：

其中E(T,，u)是字典學習正則項,，G(u)是加權TV正則項，y=Φu是數(shù)據(jù)約束項,。

2.1 基于熵約束的字典學習正則項

    稀疏表示是影響圖像重構質量的關鍵因素,，為克服傳統(tǒng)變換不能有效表示輪廓、紋理,、振蕩等高維幾何特征的缺點,，稀疏表示的研究從正交基擴展到過完備字典。式(4)中的第一項E(T,，u)是字典學習約束項,，字典學習方法一般可通過優(yōu)化下式獲取：

    在稀疏編碼過程中會得到非零系數(shù)和相對應的位置索引,，這些索引值有很大的隨機性,，導致其信息熵非常高,，降低了字典學習效率。為此,，引入熵的約束,，以提高字典學習效率。對保真項,、稀疏度以及原子選擇的熵作聯(lián)合優(yōu)化,，構造新的優(yōu)化函數(shù)：

2.2 加權各向同性與異性的TV正則項

    TV模型廣泛應用于圖像去噪、修復,、超分辨率等,其各向同性,、各向異性的數(shù)學表達如下：

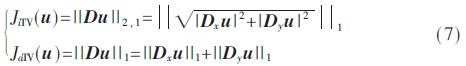
其中D_x、D_y分別表示水平和垂直方向上的導數(shù),。

    對于分段常數(shù)函數(shù)或光滑區(qū)域,，其每個像素點的梯度是1-稀疏，通過L₁范數(shù)可以很好地重構,，然而,，對于邊緣信息豐富的區(qū)域，梯度并非1-稀疏,，其效果并不理想,，它會產(chǎn)生階梯效應。針對這種非稀疏的梯度向量,，結合各向同性與各向異性,，用加權的TV正則項代替單一的TV項，即：

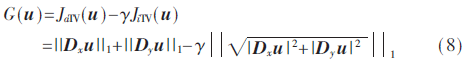
其中γ∈[0,，1],。其優(yōu)點在于具有Lipschitz正則性，并且在求解時用現(xiàn)有的算法可充分確保其收斂性,。

2.3 基于字典學習和加權TV的重構模型

    結合上述字典學習和TV模型,，構建如下重構模型：

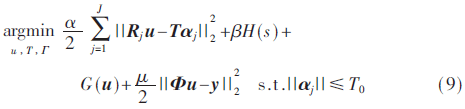
    式(9)第一項保證圖像塊可以用過完備字典稀疏表示，R_j∈R^n×N表示提取圖像u的第j塊的二值矩陣,，那么所有圖像塊的組合能覆蓋整個圖像,，可能有重疊部分，這里的圖像塊大小和過完備字典中的原子大小必須是一致的,，才能保證每個圖像塊都能被字典中的原子線性表示,。第二項是字典原子熵約束項，提高字典學習效率,。第三項是基于加權的TV正則項,，有效保留圖像邊緣信息，可抑制階梯效應,。前三項起到去除采樣過疏導致偽影和保留圖像局部結構的作用,。第四項是數(shù)據(jù)保真項,，用于增強k空間的數(shù)據(jù)保真度，其中是感知矩陣,，P是采樣矩陣,，是傅里葉變換。

3 模型求解

    本文采用交替最小化方法求解式(9),。首先固定u,，獲得學習字典和稀疏系數(shù)。然后,，固定字典和系數(shù),依據(jù)測量數(shù)據(jù)更新重構圖像u,。

    (1)字典學習階段對應的子問題目標函數(shù)為：

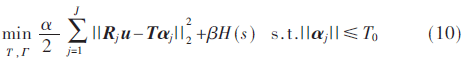
    采用K-SVD方法求解，其相應的OMP算法需要修改,，在每次迭代計算殘差時應加入選擇原子熵,，即：

    (2)更新重構階段對應的子問題目標函數(shù)為：

    上述能量泛函是凸的,，通過交替迭代轉化為求解關于u,、d的兩個子問題。

    對u問題,，利用變分法直接求導,，引入周期性邊界條件,并使用快速傅里葉變換(FFT)進行求解，可得：

4 仿真實驗與結果分析

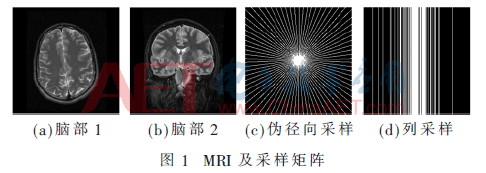
    實驗環(huán)境為MATLAB 2011a版本,，為了能夠有效對比重構圖像的不同特征,，選取光滑和紋理區(qū)域差異較大的兩張腦部圖像，尺寸為256×256,，并采用兩種不同的采樣方式,，如圖1所示。實驗中待重構數(shù)據(jù)是模擬對原始圖像的二維離散傅里葉變換,，采樣得到,。本文與字典模型、TV模型作對比,，以信噪比(SNR),、峰值信噪比(PSNR)、結構相似度(SSIM)作為指標衡量重構效果,。圖像塊大小為８×８,，字典原子維數(shù)M=64，個數(shù)K=256,，以離散余弦變換字典為初始字典,，平衡參數(shù)α=1，β=1,，稀疏度T₀=10,，λ=140,，分別取γ=0.5、1,，迭代10次,。

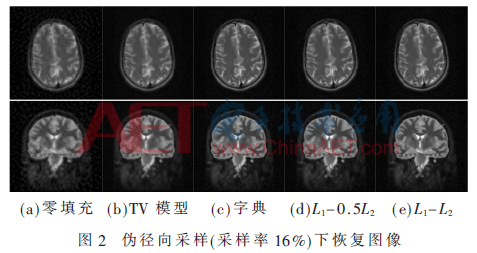
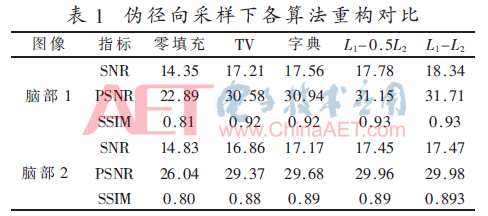
    利用零填充、TV,、字典學習3種不同算法,，分別對兩幅不同特征的MRI圖像在16%和25%采樣率下進行了多組實驗，實驗結果如圖2,、圖3所示,。不同圖像重構下SNR、PSNR,、SSIM指標對比見表1,、表2。從實驗結果看,，TV算法會對圖像邊緣信息過平滑,，丟失紋理細節(jié)信息。同時,，為了對比本文算法在不同采樣矩陣下的恢復效果,。綜合數(shù)據(jù)看，L₁-L₂恢復效果優(yōu)于L₁-0.5L₂的效果,，本文算法重構的圖像比TV或字典模型PSNR平均高出1～2 dB,，在平滑區(qū)和邊緣紋理區(qū)處理結果都優(yōu)于單純的TV和字典算法。

5 結論

    本文基于圖像塊稀疏性提出一個自適應的字典學習框架,，該框架直接由采樣的空間數(shù)據(jù)獲得,，對圖像樣本具有自適應性，又結合加權TV正則項,，充分地利用各自的優(yōu)點,，有效消除噪聲，保留圖像邊緣紋理,，增強局部結構,。實驗結果表明，本文對噪聲具有魯棒性,，在無噪聲和有噪聲的情況下均具有良好的性能,。在高度欠采樣下，圖像的各種特征有很好的重構效果,，算法經(jīng)過少量的迭代就可以收斂,，對參數(shù)的選取同樣具有魯棒性。下一步將從參考圖像出發(fā)，選擇合適初始字典,考慮低秩流形結構和塊稀疏字典兩者相結合,，使MRI重構圖像具有更豐富的結構信息,。

參考文獻

[1] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory，2006,，52(4)：1289-1306.

[2] CANDES E J.Compressive sampling[J].Marta Sanz Solé,，

     2006，17(2)：1433-1452.

[3] CANDES E J,，ROMBERG J,，TAO T.Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006,，52(2)：489-509.

[4] LUSTIG M,，DONOHO D，PAULY J M.Sparse MRI：The application of compressed sensing for rapid MR imaging[J].Magnetic Resonance in Medicine,，2007,，58(6)：1182-95.

[5] DABOV K，F(xiàn)OI A,，KATKOVNIK V,，et al.Image denoising by sparse 3-D transform-domain collaborative filtering[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society，2007,，16(8)：2080-2095.

[6] AKCAKAYA M,，BASHA T A,，GODDU B,，et al.Low-dimensional-structure self-learning and thresholding：Regularization beyond compressed sensing for MRI Reconstruction[J].Magnetic Resonance in Medicine Official Journal of the Society of Magnetic Resonance in Medicine，2011,，66(3)：756-767.

[7] RAVISHANKAR S,，BRESLER Y.MR image reconstruction from highly undersampled k-space data by dictionary learning[J].IEEE Transactions on Medical Imaging，2011,，30(5)：1028-41.

[8] RAJWADE A,，KITTLE D，TSAI T H,，et al.Coded hyper-spectral imaging and blind compressive sensing[J].Siam Journal on Imaging Sciences,，2013，6(2)：782-812.

[9] LINGALA S G,，JACOB M.A blind compressive sensing frame work for accelerated dynamic MRI[J].Proceedings,，2012，88(1)：1060-1063.

[10] KONDO S.Compressed sensing and redundant dictionaries[J].Information Theory IEEE Transactions on,，2008,，54(5)：2210-2219.

[11] RUDIN L I，OSHER S,，F(xiàn)ATEMI E.Nonlinear total variation based noise removal algorithms[J].Physica D-nonlinear Phenomena,，1992,，60(1-4)：259-268.

[12] DONG W，SHI G,，LI X,，et al.Compressive sensing via nonlocal low-rank regularization[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society，2014,，23(8)：3618-3632.

作者信息:

宋長明,，惠慶磊，程東旭

(中原工學院 理學院,，河南 鄭州450007)