侯情緣,卿粼波,滕奇志
(四川大學(xué) 電子信息學(xué)院,四川 成都 610000)
摘要:基于最大相似度的區(qū)域合并算法是一種半自動的圖像處理方式,可根據(jù)用戶提供的交互信息,利用圖像特征作為區(qū)域相似度進(jìn)行準(zhǔn)確的目標(biāo)提取。但傳統(tǒng)的MSRM算法計算量大,使用單一的圖像特征使得分割不夠精確。針對這些問題,文章對MSRM算法進(jìn)行改進(jìn),提出一種基于多特征的區(qū)域最大相似度圖像分割算法,并采用矩陣變換算法來降低計算量。該方法使用超像素圖像作為分割基礎(chǔ),首先計算圖像相鄰區(qū)域紋理和顏色特征相似度,并使用矩陣變換算法降低顏色特征矢量維度,然后計算兩種特征的權(quán)重,最后根據(jù)綜合后的相似度對圖像進(jìn)行區(qū)域合并,得到最終的顆粒提取結(jié)果。實驗結(jié)果表明,該方法可以有效提取顆粒的輪廓,提取的輪廓邊緣細(xì)節(jié)較傳統(tǒng)MSRM算法更優(yōu),算法執(zhí)行效率也得到了提高。
關(guān)鍵詞:顏色直方圖;矩陣變換;自適應(yīng)加權(quán);多特征融合
中圖分類號:TP751文獻(xiàn)標(biāo)識碼:ADOI: 10.19358/j.issn.1674-7720.2017.01.016
引用格式:侯情緣,卿粼波,滕奇志.基于多特征融合半自動巖心圖像顆粒提取[J].微型機(jī)與應(yīng)用,2017,36(1):52-55.
0引言
巖心顆粒圖像分割作為后續(xù)磨圓度、礫徑等分析的前提,對沉積儲層的研究具有重要意義[1]。傳統(tǒng)的手工分割比較精確,但費時費力,難以滿足實際需求,因此需要結(jié)合圖像分割理論使用計算機(jī)實現(xiàn)巖心顆粒目標(biāo)自動提取。
MSRM算法[2]由NING J等人于2010年提出,該算法基于最大相似度區(qū)域融合策略實現(xiàn)區(qū)域間合并,通過迭代融合實現(xiàn)目標(biāo)與背景的分離。在整個算法執(zhí)行過程中僅基于區(qū)域最大相似度合并規(guī)則完成區(qū)域合并,無需參數(shù)控制,并且分割精度高,分割性能較好[3]。但傳統(tǒng)的MSRM算法使用單一的顏色直方圖描述區(qū)域相似度,當(dāng)圖像中目標(biāo)與背景顏色過渡不明顯時算法效果不理想;而且算法計算量大,效率較低[4]。徐杰[5]等人提出先對圖像進(jìn)行細(xì)節(jié)增強(qiáng),再運用MSRM算法來提高圖像分割精度。但是該方法可能丟失圖像邊緣信息,而且算法執(zhí)行效率更低;徐少平[6] 等人則提出了IMSRM算法,該算法改用紋理特征直方圖描述相鄰區(qū)域相似度。IMSRM算法提高了算法執(zhí)行效率,但是分割精度不高。
針對上述問題,本文提出了對MSRM算法的另一種改進(jìn)算法,即綜合使用顏色和紋理特征,并通過數(shù)學(xué)模型確定不同區(qū)域兩種特征的權(quán)重,將兩種特征加權(quán)融合后作為最終的區(qū)域相似度,然后根據(jù)最終的相似度對待分割圖像進(jìn)行區(qū)域之間的合并,獲得較為準(zhǔn)確的圖像顆粒提取結(jié)果。同時,在計算顏色特征矢量矩陣時使用矩陣變換算法降低算法計算量,使得算法效率也得到有效提高。
本文中,在采用MSRM算法進(jìn)行目標(biāo)提取前,首先進(jìn)行圖像預(yù)處理和超像素圖像構(gòu)建。完成超像素分割的圖像為具有一致性圖像特征的超像素區(qū)域的集合。同時,需要用戶標(biāo)出目標(biāo)與背景的代表區(qū)域作為區(qū)域合并的先驗基礎(chǔ)。圖像經(jīng)過交互式操作被劃分為目標(biāo)、背景和未標(biāo)記三種區(qū)域的集合,使用MSRM算法就是應(yīng)用其區(qū)域融合規(guī)則來實現(xiàn)對未標(biāo)記區(qū)域集合的分配和修正,逐步將未標(biāo)記區(qū)域歸并到目標(biāo)區(qū)域和背景區(qū)域,當(dāng)未標(biāo)記區(qū)域全部歸并到目標(biāo)或背景區(qū)域時,認(rèn)為圖像分割完成。
1多特征相似度測量
在完成超像素圖像分割并且標(biāo)記出主體和背景之后,MSRM算法采用一種自適應(yīng)于圖像內(nèi)容的區(qū)域融合策略,即通過計算各區(qū)域與相鄰區(qū)域之間的相似度,利用融合規(guī)則將未標(biāo)記區(qū)域合并到背景或主體區(qū)域[4]。MSRM算法使用顏色特征衡量兩個區(qū)域之間的相似度,然后根據(jù)融合規(guī)則進(jìn)行區(qū)域合并。當(dāng)圖像中目標(biāo)與背景顏色過渡不明顯時,利用單一的顏色直方圖計算區(qū)域相似度,圖像分割效果不理想,尤其對于色彩相對單調(diào)的巖心圖像,往往會導(dǎo)致目標(biāo)提取不夠準(zhǔn)確。紋理特征不同于顏色特征,主要反映像素灰度級空間分布特征 [6],是圖像另一種重要的屬性。因此本文綜合使用顏色和紋理特征作為區(qū)域相似度描述符,首先用巴氏系數(shù)分別計算顏色和紋理特征矢量矩陣,然后自適應(yīng)加權(quán)融合兩種特征得到最終的區(qū)域相似度。
1.1特征值計算
本文計算區(qū)域之間的相似度融合采用顏色特征和紋理特征。MSRM算法中將三通道彩色圖像量化為單通道特征矩陣[2]。3個通道的N階量化,將整個RGB顏色空間劃分為N3種顏色的組合。經(jīng)過實驗,綜合考慮時間效率和提取精度,選擇N等于16。首先計算各區(qū)域的顏色直方圖,然后采用巴氏系數(shù)(Bhattacharyya Coefficient)來衡量兩個顏色直方圖之間的相似度[7]。如果把區(qū)域R的顏色直方圖記為HistcR,那么可以定義出區(qū)域R和區(qū)域Q的相似度ρc(R,Q)為:

其中,HistucR和HistucQ分別是在區(qū)域R和區(qū)域Q中顏色u出現(xiàn)的概率,u為灰度量化值。ρc(R,Q)越接近1,代表兩區(qū)域的直方圖相似度越高,即兩區(qū)域差異越小;反之,兩區(qū)域的直方圖相似度就越低,表現(xiàn)在圖像上的差異就越大。
紋理特征使用灰度共生矩陣(GLCM)表達(dá)[8],GLCM描述了在某個方向上相隔固定值的兩個像素點灰度值為t的概率。計算GLCM,首先需要將原彩色圖像轉(zhuǎn)化為灰度圖像,轉(zhuǎn)換后的圖像灰度級為0~255,此時GLCM大小為256×256。大的灰度等級更有利于表達(dá)圖像特征[8],但是也會使計算時間呈幾何級數(shù)增長。一般取S為32,創(chuàng)建大小為S×S的灰度共生矩陣GLCM(θ,d),統(tǒng)計在θ方向上相隔距離為d的像素點對的每種取值在圖像中出現(xiàn)的頻率。本文取d為1,分別計算θ為0°、45°、90°、135°時的區(qū)域GLCM(θ,d),得到圖像的水平、垂直、主對角線和副對角線4個方向的灰度共生矩陣。分別計算每個灰度共生矩陣的能量(fASM)、反差(fCON)、熵(fENT)、相關(guān)性(fCOR)4個特征,經(jīng)過歸一化后組成大小為4×4的二維特征矩陣FGLCM=(FASM,FCON,FENT,FCOR)T,用來表征圖像的紋理特征。
得到區(qū)域的FGLCM矩陣后,同計算顏色特征相似度一樣。區(qū)域R和區(qū)域Q之間紋理相似度ρt(R,Q)定義為:
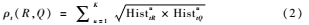
式(2)中的HistutR和HistutQ分別表示在區(qū)域R和區(qū)域Q中GLCM特征值u出現(xiàn)的概率。本文中,GLCM直方圖維數(shù)K大小為4×4,下標(biāo)中t代表紋理。
1.2多特征自適應(yīng)融合
在一幅圖像中,存在紋理特征明顯的區(qū)域和顏色特征明顯的區(qū)域[9]。所以在本文中,用公式計算每種特征在不同區(qū)域所占總相似度的權(quán)重,在一幅圖像中自適應(yīng)地確定兩種特征的權(quán)重。設(shè)w(t|R)和w(c|R)為在區(qū)域R中紋理特征和顏色特征所占的權(quán)重。
計算顏色和紋理特征權(quán)重時,首先計算該區(qū)域梯度幅值的歸一化得到直方圖G,再使用式(3)計算G的稀疏度S:
![08WOH$XH8EJRZ])[`%V1@RA.png 08WOH$XH8EJRZ])[`%V1@RA.png](http://files.chinaaet.com/images/2017/03/02/6362407476440093284862122.png)
其中,n為直方圖的維數(shù),這里n為256。Gp代表G的lp范數(shù)。這里計算梯度采用Roberts模板[10]:

其中f(x,y)為灰度化后的點(x,y)處的像素值。然后使用對數(shù)函數(shù)對顏色特征權(quán)重進(jìn)行建模:

其中a和b為常數(shù),可以通過實驗、訓(xùn)練的方法進(jìn)行估算,根據(jù)文獻(xiàn)[10]中實驗參數(shù),選擇a=41.9,b=37.2。w(c|R)的值越接近1,則在該區(qū)域中顏色所占權(quán)重越大。對于兩個區(qū)域R和Q,采用式(6)融合兩個概率。
w(c|R,Q)=min(w(c|R),w(c|Q))(6)
w(t|R,Q)=1-w(c|R,Q)(7)
總區(qū)域相似度ρ(R,Q)由顏色相似度ρc(R,Q)和紋理相似度ρt(R,Q)由式(8)通過加權(quán)融合獲得:
ρ(R,Q)=w(c|R,Q)ρc(R,Q)+w(t|R,Q)ρt(R,Q)(8)
MSRM算法使用由顏色和紋理特征加權(quán)融合而得的相似度作為合并準(zhǔn)則更加合理,也使后續(xù)的分割更加準(zhǔn)確。
2矩陣變換
MSRM算法的核心思想就是相似區(qū)域的合并規(guī)則,從而也決定了算法在執(zhí)行過程中需要反復(fù)衡量計算相鄰區(qū)域間的相似度[4]。
在測量相鄰區(qū)域間顏色特征相似度時,MSRM算法通過對彩色圖像R、G、B 3個通道進(jìn)行16階量化,將整個RGB顏色空間劃分為163種顏色的組合,則每個區(qū)域顏色直方圖特征矢量長達(dá)4 096維。反復(fù)應(yīng)用巴氏系數(shù)進(jìn)行直方圖相似度衡量運算將直接限制MSRM算法的運行效率。因此,本文提出使用矩陣變換算法來降低顏色直方圖特征矢量維數(shù),提升MSRM算法的運行效率。
通過式(2)可以看出,如果N3維的顏色直方圖特征矢量中包含0值,那么0值與任何值的乘積加和將不會對區(qū)域間的相似度造成任何變化。事實上,根據(jù)文獻(xiàn)[4]對不同圖像N階量化后的顏色組合統(tǒng)計,在自然彩色圖像中,三通道顏色的組合數(shù)目將遠(yuǎn)低于16階量化后的顏色組合;針對巖心圖像,實際的顏色組合數(shù)目將更低。也就是說運算過程包含了大量無用的0值,降低了算法運行效率。
矩陣變換算法可以簡單有效地剔除特征矢量中的0值,應(yīng)用于MSRM算法中,將使得算法的運行效率得到大幅度提升。矩陣變換算法基本步驟為:首先構(gòu)建一個表示灰度值的數(shù)組并初始化為-1和一個變量Num初始化為0。然后依次取原圖顏色值,讀取數(shù)組中以該值為下標(biāo)對應(yīng)的元素值,若為-1,將原圖中灰度值賦值為Num,然后Num增加1;若不為-1,以數(shù)組中的值賦值為原圖灰度值,依次統(tǒng)計變換,最后返回變換后的顏色特征矩陣和Num值。
返回的矩陣即為剔除冗余數(shù)據(jù)的圖像數(shù)據(jù),Num值為彩色圖像中所包含顏色組合的實際個數(shù)。圖1給出了矩陣變換的示意圖:左邊矩陣內(nèi)數(shù)據(jù)是截取自圖像的局部數(shù)據(jù),右邊是經(jīng)過變換后的矩陣數(shù)據(jù)。
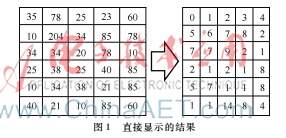
可以發(fā)現(xiàn)變換后的矩陣相當(dāng)于對原始數(shù)據(jù)進(jìn)行了重排,除去了冗余數(shù)據(jù),使特征矢量的維度由N3降低為Num,此時可由式(9)計算顏色特征相似度。
![IQZGX7@5_94]Q4(ZP(P66D9.png IQZGX7@5_94]Q4(ZP(P66D9.png](http://files.chinaaet.com/images/2017/03/02/6362407478887132062599107.png)
3實驗結(jié)果與分析
3.1矩陣變換后的圖像特征矢量維度
矩陣變換后特征矢量維度變?yōu)镹um, 對不同圖像進(jìn)行16階灰度量化并對每個通道的顏色組合進(jìn)行統(tǒng)計,對比見表1。

對圖像大小為974×735的巖心圖像1進(jìn)行性能測試,最大相似度區(qū)域融合算法的運行時間隨顏色直方圖特征矢量維度變化的曲線如圖2所示。
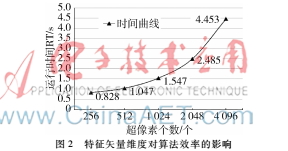
從表1中可以看出,經(jīng)過數(shù)據(jù)重排,特征矢量維度降低了10倍左右。由于數(shù)據(jù)重排是剔除特征矢量中的0值,所以不會影響運算結(jié)果,從圖2中可以看出數(shù)據(jù)越小,時間越少。所以經(jīng)過矩陣變換,在不影響精確度的同時使得算法效率得到提升。
3.2優(yōu)化后算法的整體性能
在本文中進(jìn)行圖像分割,第一步對圖像進(jìn)行預(yù)處理,第二步進(jìn)行超像素的構(gòu)建,然后添加目標(biāo)和背景交互標(biāo)記,最后使用MSRM算法進(jìn)行圖像分割,可以多次添加交互標(biāo)記,進(jìn)行目標(biāo)提取。圖3為對真實巖心圖像進(jìn)行顆粒提取的過程。

算法分割精度與算法執(zhí)行效率是衡量算法分割性能的重要依據(jù)。分割效果可以使用交互頻繁程度(FOI)、分割差異率(SDR)、邊界偏離誤差(BDE)三個標(biāo)準(zhǔn)進(jìn)行衡量。交互頻繁程度越低,分割差異率和邊界偏離誤差越小,表明分割性能越好[11]。表2為對圖3(e)和(f)兩圖評價指標(biāo)數(shù)據(jù)。由表2的數(shù)據(jù)對比可以看出,改進(jìn)后的算法交互頻繁程度低,分割差異率和邊界偏離誤差更小。因此本文改進(jìn)算法可以產(chǎn)生更為便捷的分割過程和更為準(zhǔn)確的分割結(jié)果,從而減少交互操作,給巖心圖像顆粒提取帶來更多方便。

參考文獻(xiàn)
[1] 任輝.巖心粒度分割算法的研究與實現(xiàn)[D].荊州:長江大學(xué),2013.
[2] NING J F,ZHANG L,ZHANG D,et al.Interactive image segmentation by maximal similarity based region merging[J].Pattern Recogn,2010,43(2):445456.
[3] He Jia, KIM C S,C. KUO C C J.Interactive segmentation techniques[M].Springer,2013.
[4] 李朝輝.巖心圖像顆粒提取算法研究與實現(xiàn)[D].成都:四川大學(xué),2015.
[5] 徐杰,許存祿,邢磊,等.改進(jìn)的最大相似度區(qū)域目標(biāo)分割算法[J].計算機(jī)工程與設(shè)計,2015,36(9):25192523.
[6] 徐少平,劉小平,李春泉.基于區(qū)域最大相似度的快速圖像分割算法[J].光電子激光,2013,24(5):990998.
[7] 唐超,交互式圖像分割相關(guān)技術(shù)研究[D].成都:電子科技大學(xué),2014.
[8] 苑麗紅,付麗,楊勇,等. 灰度共生矩陣提取紋理特征的實驗結(jié)果分析[J].計算機(jī)應(yīng)用,2009,29(4):10181021.
[9] 鄭慶慶.紋理特征提取及其在圖像分割中的應(yīng)用研究[D].武漢:華中科技大學(xué),2011.
[10] 劉麗,匡綱要.圖像紋理特征提取方法綜述[J].中國圖象圖形學(xué)報,2009,14(4):622635.
[11] 張毓晉.圖像分割評價技術(shù)分類和比較[J].中國圖象圖形學(xué)報, 1996,1(2):151157.

