文獻標識碼: A
文章編號: 0258-7998(2014)03-0104-04
目前,相控陣天線已經(jīng)廣泛應用于軍事、民用領域,它通過改變陣元激勵信號的相位來改變天線方向圖波束指向。天線的輻射能力可以用方向圖函數(shù)來描述,方向圖的取值與陣元間距有關,增大陣元間距即增加了天線孔徑長度,可使天線波束變窄,提高天線分辨率。但是對于固定的工作頻率和掃描角,若陣元間距過大,陣列天線掃描時的輻射場,除主瓣以外在其他方向會因場強同相疊加形成強度與主瓣相仿的輻射瓣,稱之為柵瓣。柵瓣占據(jù)了輻射能量,使天線增益降低。從柵瓣“看”到的目標與主瓣“看”到的目標易于混淆,導致目標位置模糊。干擾信號從柵瓣進入接收機將影響通信系統(tǒng)的正常工作[1]。因此,應合理地選擇相控陣天線的陣元間距避免出現(xiàn)柵瓣。許多文章只注重對線陣柵瓣進行分析[2-3],而很少分析平面陣柵瓣問題。本文對平面陣天線柵瓣性能進行分析并通過仿真驗證。
1 陣列天線方向圖函數(shù)模型
單個天線的方向性是有限的,可以將若干個單元天線按一定方式排列組合形成天線陣列來加強天線的定向輻射能力。平面陣天線陣元有不同的排列方式,常見的陣型有矩形排列平面陣和三角形排列平面陣。無論哪種陣型,其方向圖函數(shù)模型都是相同的。
為簡化分析,本文做以下假設[4]:(1)所有陣元為均勻幅度加權,即信號到達不同陣元時沒有幅度變化;(2) 陣元都是相同的全向天線且各陣元之間無互耦;(3)所有入射信號均為遠場信號,以平面波波前到達陣列;(4)入射到陣列上的信號帶寬遠小于信號載波頻率。

一個陣元構成的陣列如圖1所示。圖中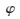 為方位角,取值范圍為0~2,
為方位角,取值范圍為0~2,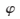 為俯仰角,取值范圍為0~0.5。如果用矢量a表示信號來向,pl表示第l個陣元坐標,則第l個陣元接收信號相對于原點陣元接收信號的時延為l=aTpl/c,其中,c為光速[5]。
為俯仰角,取值范圍為0~0.5。如果用矢量a表示信號來向,pl表示第l個陣元坐標,則第l個陣元接收信號相對于原點陣元接收信號的時延為l=aTpl/c,其中,c為光速[5]。
![46YRI_7O5X5A4P5]23HOION.png 46YRI_7O5X5A4P5]23HOION.png](http://files.chinaaet.com/images/2017/01/16/6362017596380253855585230.png)
則第l個陣元接收信號相對于原點陣元接收信號的相位差為l=kTpl,此時信號方向矢量為方位角和俯仰角的函數(shù),可表示為:

在數(shù)字化實現(xiàn)的相控陣加權中,權矢量等于期望信號的方向矢量:
![937R_6_U4K]~W4}]%Y9045Q.png 937R_6_U4K]~W4}]%Y9045Q.png](http://files.chinaaet.com/images/2017/01/16/6362017605242853853200375.png)
其中, 0和?
0和? 0分別為天線波束最大指向的俯仰角與方位角。
0分別為天線波束最大指向的俯仰角與方位角。
根據(jù)陣列天線方向圖乘積定理,方向圖等于陣元因子pE![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017686602653858536300.png) 與陣元因子pA
與陣元因子pA![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017687099153853122480.png) 二者的乘積,即[6]:
二者的乘積,即[6]:

因陣元都是相同的全向天線,所以場強方向圖為:

式中,符號‖‖為模值。
2 平面陣列天線柵瓣性能分析
2.1 矩形排列平面陣
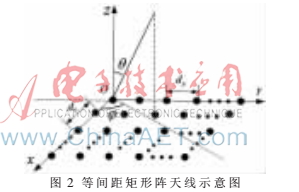
等間距矩形陣天線示意圖如圖2所示,一個共有M×N個天線單元的天線陣列位于xoy平面上,天線單元沿x和y方向的間距分別為dx和dy。
為簡化分析本文做以下代換:
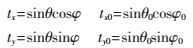
根據(jù)式(5)得知矩形排列平面陣的權矢量為:
![]~C8ZSVEG`O}`9}{PM6SQ`9.png ]~C8ZSVEG`O}`9}{PM6SQ`9.png](http://files.chinaaet.com/images/2017/01/16/6362017611172453858604798.png)
令
Tx=tx-tx0, Ty=ty-ty0
因不考慮幅度加權,則根據(jù)式(7)可得矩形陣天線的方向圖函數(shù)[7-9]:
![ZAN{)Q({]HQQ5S1V)AL805B.png ZAN{)Q({]HQQ5S1V)AL805B.png](http://files.chinaaet.com/images/2017/01/16/6362017615175853854499131.png)
由上式可知,矩形陣天線方向圖可以看成兩個線陣天線方向圖的乘積,矩形陣天線方向圖要取得最大值必須滿足以下條件:

式中p和q為整數(shù)。
由式(10)可得在球坐標系(?茲,?漬)中的主瓣、柵瓣位置滿足以下公式:
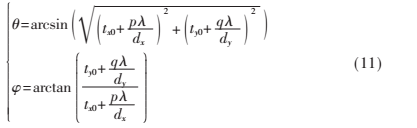

![4W8CA(Q6RW282ZH0`SV]L)O.png 4W8CA(Q6RW282ZH0`SV]L)O.png](http://files.chinaaet.com/images/2017/01/16/6362017647144553858726681.png)
2.2 三角形排列平面陣

三角形排列平面陣可以看成兩個矩形陣交錯排列之和[10],如圖3所示。天線陣列位于xoy平面上,為了便于區(qū)分,兩個矩形陣列的陣元分別用黑色圓點和黑色正方形表示。兩矩形陣沿x和y方向的間距分別為2dx和2dy,亦即相鄰兩陣元之間沿x方向的距離為dx,沿y方向的距離為dy。若dx=dy,則三角形為等腰直角三角形;若dy=dx,則三角形為等邊三角形。
由于這兩個矩形陣的參考點在x軸方向與y軸方向的位置偏差分別為dx和dy,故整個陣列的方向圖函數(shù)可表示為:

因此,三角形排列平面陣的方向圖取最大值取決于以下兩個條件:
(1) 滿足式

式中p和q為整數(shù)。
(2) 滿足p+q=偶數(shù)。
若p+q=奇數(shù),則由式(14)可知綜合因子方向圖B1![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017700002853854248752.png) 等于0,根據(jù)式(13)由方向圖乘積定理可得整個三角形陣列的方向圖函數(shù)B
等于0,根據(jù)式(13)由方向圖乘積定理可得整個三角形陣列的方向圖函數(shù)B![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017700521353855094363.png) 也等于0,不會出現(xiàn)最大值。若p+q=偶數(shù),綜合因子方向圖B1
也等于0,不會出現(xiàn)最大值。若p+q=偶數(shù),綜合因子方向圖B1![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017701139053858822502.png) )取最大值,則整個三角形陣列的方向圖函數(shù)
)取最大值,則整個三角形陣列的方向圖函數(shù)![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017702487953856215293.png) 將取最大值。
將取最大值。
由以上分析可知,在球坐標系![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017702890253859471433.png) 中的主瓣、柵瓣位置滿足公式:
中的主瓣、柵瓣位置滿足公式:
![ZZ[K$[}J987N2{2]%4X4S44.png ZZ[K$[}J987N2{2]%4X4S44.png](http://files.chinaaet.com/images/2017/01/16/6362017634830753859525555.png)
當可知T平面上的點恰好就是球坐標系![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017707825153857501450.png) 中單位球面上的點在T平面上的投影。因‖T‖=|sin
中單位球面上的點在T平面上的投影。因‖T‖=|sin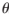 |,在T平面單位圓以內(nèi)的區(qū)域滿足‖T‖=|sin
|,在T平面單位圓以內(nèi)的區(qū)域滿足‖T‖=|sin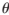 |≤1,即對應球坐標系
|≤1,即對應球坐標系![1SSE{]C0S)%PLBVSW~8F)}T.png 1SSE{]C0S)%PLBVSW~8F)}T.png](http://files.chinaaet.com/images/2017/01/16/6362017708286253851467669.png) ,此時波束位于可見區(qū),稱為實空間。單位圓以外的區(qū)域稱為虛空間,即不可見區(qū)。對于相控陣天線要求實空間內(nèi)方向圖只有一個最大值,即主瓣。相控陣天線波束處于掃描狀態(tài)時,在T平面上表現(xiàn)為主瓣從原點到T0點的平移,且所有的柵瓣亦做相同的平移。
,此時波束位于可見區(qū),稱為實空間。單位圓以外的區(qū)域稱為虛空間,即不可見區(qū)。對于相控陣天線要求實空間內(nèi)方向圖只有一個最大值,即主瓣。相控陣天線波束處于掃描狀態(tài)時,在T平面上表現(xiàn)為主瓣從原點到T0點的平移,且所有的柵瓣亦做相同的平移。

利用方向余弦平面Tx-Ty來描述天線柵瓣特性,則三角形排列平面陣天線柵瓣在Tx-Ty平面上的位置及其移動如圖4所示。從圖中可看出波束掃描時要想在可見,要使空間不出現(xiàn)柵瓣,須滿足Tx-Ty平面上柵瓣與主瓣間的最小距離大于1+sin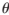 0[11]。
0[11]。
對于等腰直角三角形陣列,不出現(xiàn)柵瓣的條件為:
![_C(NSBW(GBP6{]0TWH~G{OK.png _C(NSBW(GBP6{]0TWH~G{OK.png](http://files.chinaaet.com/images/2017/01/16/6362017712023353857051915.png)
3 仿真結果及分析
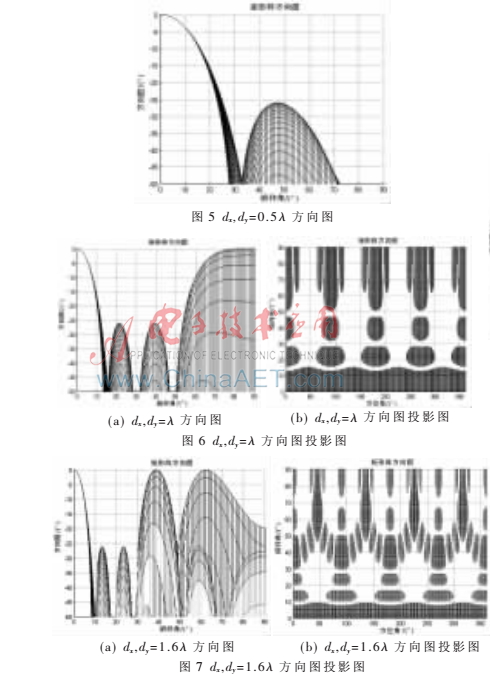
3.1 矩形排列平面陣
 出現(xiàn)多個柵瓣,柵瓣位置也可由式(11)驗證。綜合圖5、圖6和圖7可知隨著陣元間距的增大,天線波束逐漸變窄,柵瓣個數(shù)增加。
出現(xiàn)多個柵瓣,柵瓣位置也可由式(11)驗證。綜合圖5、圖6和圖7可知隨著陣元間距的增大,天線波束逐漸變窄,柵瓣個數(shù)增加。
3.2 三角形排列平面陣
以等腰直角三角形為例,設定天線波束最大指向角為 0=0、
0=0、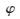 0=0,天線陣元數(shù)為18,根據(jù)式(19)得出等腰直角三角形排列平面陣不出現(xiàn)柵瓣的條件為dx<0.707
0=0,天線陣元數(shù)為18,根據(jù)式(19)得出等腰直角三角形排列平面陣不出現(xiàn)柵瓣的條件為dx<0.707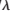 、dy<0.707
、dy<0.707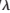 。首先,圖8顯示時天線波束沒有柵瓣;其次,由式(18)可計算出dx,dy=0.707
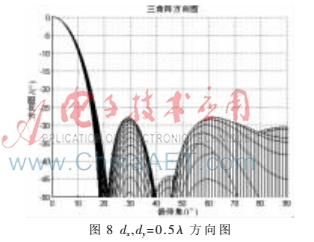
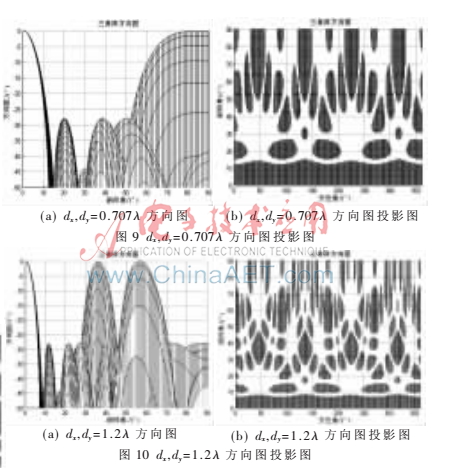
。首先,圖8顯示時天線波束沒有柵瓣;其次,由式(18)可計算出dx,dy=0.707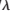 時柵瓣的位置:時天線波束出現(xiàn)多個柵瓣,柵瓣位置也可由式(18)驗證。綜合圖8、圖9和圖10可知,隨著陣元間距的增大,天線波束逐漸變窄,柵瓣個數(shù)增加。
時柵瓣的位置:時天線波束出現(xiàn)多個柵瓣,柵瓣位置也可由式(18)驗證。綜合圖8、圖9和圖10可知,隨著陣元間距的增大,天線波束逐漸變窄,柵瓣個數(shù)增加。
本文根據(jù)相控陣天線原理推導出平面陣列天線方向圖出現(xiàn)柵瓣的位置與波長、陣元間距d以及波束指向(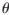 0,
0,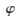 0)的數(shù)學關系以及不出現(xiàn)柵瓣的陣元間距的取值范圍,然后運用MATLAB仿真進行驗證。仿真結果表明,當工作頻率以及波束指向確定之后,只要調(diào)整陣元間距使其在不出現(xiàn)柵瓣的取值范圍內(nèi),就可有效避免天線方向圖出現(xiàn)柵瓣。仿真結果驗證了理論推導的正確性,對工程應用具有指導意義。
0)的數(shù)學關系以及不出現(xiàn)柵瓣的陣元間距的取值范圍,然后運用MATLAB仿真進行驗證。仿真結果表明,當工作頻率以及波束指向確定之后,只要調(diào)整陣元間距使其在不出現(xiàn)柵瓣的取值范圍內(nèi),就可有效避免天線方向圖出現(xiàn)柵瓣。仿真結果驗證了理論推導的正確性,對工程應用具有指導意義。
參考文獻
[1] 束咸榮,何炳發(fā),高鐵.相控陣雷達天線[M]. 北京:國防工業(yè)出版社,2007:16-17.
[2] WOOH S C, SHI Y. A Simulation study of the beamsteering characteristics for linear phased arrays[J]. Journal of Nondestructive Evaluation, 1999,18(2):39-42.
[3] ABDEL M. Grating lobe suppression in uniformly spacedlinear phased arrays[C].National Radio Science Conference. New Cairo, 2009:1-10.
[4] 付曉蕾.智能天線DOA估計及自適應波束形成技術研究[D].重慶:重慶大學,2007.
[5] 劉玲,劉曉明,曾浩.基于MATLAB的陣列信號處理仿真方法[J].系統(tǒng)仿真學報,2008,20(13):3548-3549.
[6] Lu Bao, Gong Shuxi, Zhang Shuai, et al. Optimum spatial arrangement of array elements for suppression of grating-lobes of radar cross section[J]. IEEE Antennas and Wire-less Propagation Letters, 2010(9):114-117.
[7] 陳志杰,李永禎,戴幻堯. 相控陣天線方向圖的建模與實時仿真方法[J].計算機仿真,2011,28(3):31-35.
[8] 鄭美燕, 陳客松. 基于增廣矩陣束方法的平面天線陣列綜合[J]. 電子技術應用,2012,38(12):101-102.
[9] WHEELER H A. The grating-lobe series for the Imped-ance variation in a planar phased-array antenna[J]. IEEE Transactions on Antennas and Propagation, 1966,14(6): 707-714.
[10] 張光義.相控陣雷達原理[M].北京:國防工業(yè)出版社,2009.
[11] HANSEN R C. Phased array antennas[M]. New Jersey: John Wiley & Sons, Inc., 2009.

