王寧章,，閔仁江,，許慧青

　　（廣西大學(xué) 計(jì)算機(jī)與電子信息學(xué)院,，廣西 南寧 530004）

       摘要：在自適應(yīng)波束形成中,，由于期望信號(hào)(SOI)導(dǎo)向矢量(SV)的誤差、采樣點(diǎn)數(shù)較少,、訓(xùn)練數(shù)據(jù)中存在期望信號(hào)成分等原因,，造成波束形成的性能嚴(yán)重下降。針對(duì)以上問題,，提出了一種穩(wěn)健波束形成方法,。首先利用MUSIC算法和參數(shù)估計(jì)來重構(gòu)不包含SOI的干擾噪聲協(xié)方差矩陣，再通過利用相關(guān)系數(shù)來估計(jì)出期望信號(hào)導(dǎo)向矢量,。仿真結(jié)果表明,，該算法可以處理較大的方向誤差，并且信噪比(SNR)在較大的范圍內(nèi)都可以得到比傳統(tǒng)方法更佳的性能,。

　　關(guān)鍵詞：自適應(yīng)波束形成,；MUSIC算法；導(dǎo)向矢量估計(jì)

　　中圖分類號(hào)：TN911文獻(xiàn)標(biāo)識(shí)碼：ADOI：10.19358/j.issn.16747720.2016.23.018

　　引用格式：王寧章,，閔仁江,，許慧青. 基于干擾加噪聲協(xié)方差矩陣重構(gòu)的穩(wěn)健自適應(yīng)波束形成［J］.微型機(jī)與應(yīng)用，2016,35（23）：62-64,，68.

0引言

　　由于接收特定方向的信號(hào),，波束形成器可以認(rèn)為是空間濾波器,。它可以應(yīng)用在不同的信號(hào)處理領(lǐng)域，包括雷達(dá),、聲吶,、醫(yī)學(xué)成像、射電天文,、無線通信等,。作為數(shù)據(jù)依賴型波束形成器，自適應(yīng)波束形成器通過抑制信號(hào)環(huán)境中的干擾和噪聲,，提取期望信號(hào)來調(diào)整權(quán)重矢量［1］,。標(biāo)準(zhǔn)的Capon波束形成器(Standard Capon Beamformer, SCB)是大家所熟知的波束形成器，如果訓(xùn)練數(shù)據(jù)中不包含期望信號(hào)(Signal of Interest, SOI),，那么SCB可以有最優(yōu)的輸出信干噪比(SignaltoInterfaceplusNoise Ratio, SINR)和高分辨率［2］,。但是在實(shí)際的訓(xùn)練數(shù)據(jù)中經(jīng)常存在SOI。在過去的幾年中,，許多穩(wěn)健自適應(yīng)波束形成器算法被提出,，用來解決訓(xùn)練數(shù)據(jù)中存在的SOI和導(dǎo)向矢量(Steering Vector, SV)誤差問題［3-5］。

　　在文獻(xiàn)［3］中,，GU Y等人提出使用Capon空間譜積分方法,，其中積分區(qū)域?yàn)槌齋OI方向以外的角度區(qū)域，這種方法可以重構(gòu)出干擾噪聲協(xié)方差矩陣,。通過解決二次約束二次規(guī)劃(QCQP)問題來修正SOI假設(shè)的SV,。這個(gè)方法在解決方向誤差上會(huì)獲得一個(gè)很好的性能。但是該方法的復(fù)雜度很高,，并且需要知道精確的陣列結(jié)構(gòu)信息,。針對(duì)以上問題，HUANG L等人［4］提出把求不確定集合積分區(qū)域轉(zhuǎn)變?yōu)榍蟓h(huán)不確定集合積分區(qū)域以及用離散求和方法來重構(gòu)干擾噪聲協(xié)方差矩陣,。CHEN F等人［5］提出一種低復(fù)雜度的相關(guān)系數(shù)重構(gòu)方法,，通過直接使用采樣協(xié)方差矩陣的特征向量與假設(shè)的SV有最大的相關(guān)性來解決SOI的SV估計(jì)問題。這幾種方法都可以有效地提高波束形成性能,，但是它們對(duì)于SOI和干擾信號(hào)存在相關(guān)性的問題都比較敏感,，可能會(huì)造成SOI存在于重構(gòu)的干擾噪聲協(xié)方差矩陣中，造成性能急劇下降,。本文使用MUSIC算法和參數(shù)化估計(jì)優(yōu)化采樣協(xié)方差矩陣和重構(gòu)干擾噪聲協(xié)方差矩陣,，然后，對(duì)估計(jì)采樣協(xié)方差矩陣進(jìn)行特征分解和相關(guān)性分析,，得出修正的SV,。

1信號(hào)模型

　　考慮M個(gè)陣列元素組成的均勻線性陣列(Uniform Liner Array, ULA)，并接受L個(gè)遠(yuǎn)場(chǎng)的窄帶信號(hào),。窄帶波束形成器的輸出可表示為：

　　其中,，k是時(shí)間參數(shù)，x(k)=［x1(k),…,，xM(k)］T為一個(gè)M×1的陣列觀測(cè)復(fù)數(shù)矢量,，ω=［ω1,ω2,ω3,…,ωM］T是M×1的波束形成權(quán)重復(fù)數(shù)矢量，(·)T和(·)H分別代表轉(zhuǎn)置和Hermitian轉(zhuǎn)置,，觀測(cè)矢量(訓(xùn)練參數(shù))可以表示為:

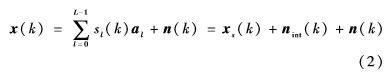
　　其中,，sl(k)和al分別代表第l次信號(hào)的波陣面和對(duì)應(yīng)的SV。xs(k)=a0s0(k),，nint(k)=∑L-1l=1alsl(k)和n(k)分別是期望信號(hào),、干擾和噪聲。

　　理論上的數(shù)據(jù)協(xié)方差矩陣可以表示為:

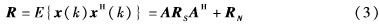
　　其中,，RS和RN分別為信號(hào)協(xié)方差矩陣和噪聲協(xié)方差矩陣,，A為空間陣列的流型矩陣(導(dǎo)向矢量陣)，且A=［a0,…,，al-1］,。對(duì)于空間理想的白噪聲且噪聲功率為σ2n，則有下式成立：

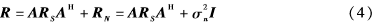
　　其中,，I是M×M的單位陣,。

　　為了測(cè)量波束形成的性能，在SOI不失真時(shí)的最大輸出SINR可以定義為:

　　其中,，

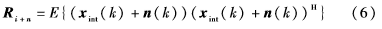
　　為M×M維干擾加噪聲協(xié)方差矩陣,，σ20為SOI的功率。使用波束形成最大輸出SINR可以得到最優(yōu)權(quán)重矢量:

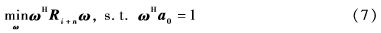
　　上述問題的最優(yōu)權(quán)重矢量為:

　　這個(gè)被稱為最小方差無畸變波束形成器(Minimum Variance Distortionless Response, MVDR)或標(biāo)準(zhǔn)Capon波束形成器(SCB),。在實(shí)際應(yīng)用中,，實(shí)際的干擾噪聲協(xié)方差矩陣Ri+n難以直接得到。因此,，可以使用采樣協(xié)方差矩陣來代替,。

　　其中，K是快拍點(diǎn)數(shù),。當(dāng)K很小時(shí),，和Ri+n的差距比較大，這會(huì)使得SOI被當(dāng)成干擾而被抑制,，特別是存在SOI導(dǎo)向矢量誤差和高輸入信噪比(Signal to Noise, SNR)時(shí),。因此估計(jì)協(xié)方差矩陣時(shí)，移除SOI部分是很有必要的,。

2提出波束形成算法

　　本文提出了一種新的自適應(yīng)波束形成算法來重構(gòu)干擾噪聲協(xié)方差矩陣,，該方法采用MUSIC算法原理和參數(shù)化估計(jì)來優(yōu)化采樣協(xié)方差矩陣以及重構(gòu)出干擾噪聲協(xié)方差矩陣。同時(shí),，該方法利用相關(guān)系數(shù)來修正估計(jì)的SV,。

　　2.1干擾加噪聲協(xié)方差矩陣重構(gòu)

　　為了重構(gòu)干擾加噪聲協(xié)方差矩陣,，基于文獻(xiàn)［6］的方法原理，公式(4)可以寫成如下形式：

　　上等式可轉(zhuǎn)化為：

　　其中,，A=(AHA)-1AH為A的偽逆矩陣,RS為非對(duì)角化的信號(hào)協(xié)方差矩陣,。當(dāng)采樣點(diǎn)數(shù)有限時(shí)會(huì)導(dǎo)致信號(hào)之間產(chǎn)生多余的相關(guān)性，或當(dāng)信號(hào)之間已經(jīng)存在相關(guān)性,，這會(huì)使得輸出SINR顯著下降,。可以使用矩陣的參數(shù)估計(jì)［7］來去掉多余的相關(guān)性,，即對(duì)RS對(duì)角化得到Rd,。由于只能得到采樣協(xié)方差矩陣，則信號(hào)協(xié)方差矩陣可以表示為:

　　對(duì)上式對(duì)角化得到:

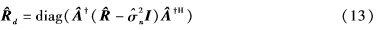
　　為了計(jì)算出,，需要知道信號(hào)的波達(dá)方向和陣列流行結(jié)構(gòu),。前文假設(shè)陣列結(jié)構(gòu)是已知的，同時(shí)使用MUSIC算法的高分辨率搜索得到估計(jì)的信號(hào)方向,。2n可以使用MUSIC算法中的最小特征值得到,，把、d和2n代入式(4)中,，得到采樣協(xié)方差矩陣的參數(shù)估計(jì):

　　上述為參數(shù)化估計(jì)后的采樣協(xié)方差矩陣,，該矩陣中的多余相關(guān)性已去除，在重構(gòu)干擾噪聲協(xié)方差矩陣時(shí),，計(jì)算結(jié)果更精確,。在角度為θ時(shí)，功率可以使用e得到:

　　使用式(15),，重構(gòu)的干擾噪聲協(xié)方差矩陣可以表示為:

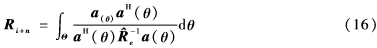
　　其中,，a(θ)是角度為θ的SV，為除期望信號(hào)角度區(qū)間外的其他區(qū)間,，由于在實(shí)際情況下,，期望信號(hào)的SV是不可獲得的，通常利用估計(jì)的SV來代替實(shí)際的SV,。所以,，下面講述期望信號(hào)估計(jì)SV的計(jì)算過程。

　　2.2期望信號(hào)SV的估計(jì)

　　在計(jì)算干擾加噪聲協(xié)方差矩陣中,，使用了MUSIC算法,，通過MUSIC算法和估計(jì)的采樣協(xié)方差矩陣e得到信號(hào)子空間和噪聲子空間，如下所示:

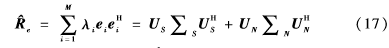
　　其中,，λi,i=1,…,，M為e的特征值并從大到小排列，ei為特征值對(duì)應(yīng)的特征向量。

　　其中,，US為信號(hào)子空間,，由于特征向量與信號(hào)的SV處于相同的空間，假設(shè)的期望信號(hào)SV可以被期望信號(hào)的特征向量來代替,?？梢允褂孟嚓P(guān)系數(shù)的定義來找出符合情況的特征向量。由于期望信號(hào)SV與期望信號(hào)的特征向量有最大的相關(guān)性,，可以用公式表示為：

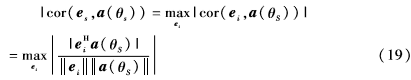
　　根據(jù)式(17)找到最大的相關(guān)系數(shù)對(duì)應(yīng)的ei，即可以得到期望信號(hào)的特征向量es,，考慮到期望信號(hào)SV的范數(shù)約束,，估計(jì)的期望信號(hào)SV可以表示為:

　　因此，權(quán)重矢量可以寫為：

　　由上可見,，算法主要的復(fù)雜度是在進(jìn)行特征分解時(shí),，復(fù)雜度為O(M3)。與前文提到的算法相比,，算法的復(fù)雜度大幅降低,，更有利于實(shí)際工程的應(yīng)用。

3仿真結(jié)果

　　本文仿真中,，考慮一個(gè)間隔半波長(zhǎng)的全方向天線陣元M=10的均勻線陣,。假設(shè)有估計(jì)的3個(gè)信號(hào)沖擊信號(hào)分別為θ0=5°，θ1=20°,，θ2=50°,，噪聲模型為一個(gè)復(fù)數(shù)高斯白噪聲。第一個(gè)信號(hào)為期望信號(hào),，其他兩個(gè)信號(hào)為干擾信號(hào),，它們的干噪比為10 dB。假設(shè)SOI和干擾的角度區(qū)域分別為Θ0=［θ0-5°,θ0+5°］,、Θ1=［θ1-5°,θ1+5°］和Θ2=［θ2-5°,θ2+5°］,，除SOI的補(bǔ)集為=［-90°，0°）∪（10°,，90°］,。對(duì)于所有的情況，平均進(jìn)行了200次MonteCarlo實(shí)驗(yàn),。

　　將本文的方法分別與對(duì)角加載算法［8］,、特征空間算法［9］、最差性能優(yōu)化算法［10］,、重構(gòu)算法［3］和低復(fù)雜度重構(gòu)算法［5］相比較,。在仿真中，假設(shè)從信號(hào)源接收的每個(gè)信號(hào)與實(shí)際信號(hào)存在［-5°,，5°］的差別,，這個(gè)假設(shè)可以表示隨機(jī)的方向誤差,，再使用公式(8)計(jì)算出最優(yōu)SINR。

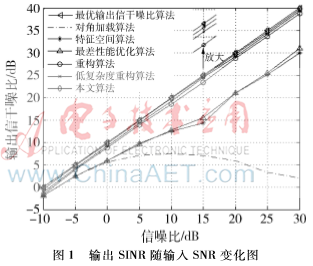
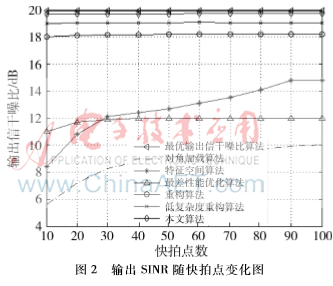
　　圖1為存在信號(hào)方向誤差的輸出SINR隨輸入SNR變化圖,，快拍點(diǎn)數(shù)固定為30,。從圖中可以看出，對(duì)角加載算法,、特征空間算法,、最差性能優(yōu)化算法在SNR較高時(shí)，輸出SINR明顯低于其他4種算法,；本文提出的算法在低SNR和高SNR時(shí)都有高于其他算法的輸出SINR,，以SNR為15 dB為例，與最優(yōu)輸出SINR算法相差僅0.3 dB左右,。因此,，本文算法的高性能可以使得波束形成的穩(wěn)健性有較大的提升。圖2為存在信號(hào)方向誤差的輸出SINR隨快拍點(diǎn)數(shù)變化圖,，SNR固定在10 dB,，顯而易見，在快拍數(shù)變化中,，本文算法有穩(wěn)定的輸出SINR,，并且比其他算法有更高的輸出SINR。

4結(jié)論

　　本文提出一種新穎的干擾加噪聲協(xié)方差矩陣重構(gòu)的穩(wěn)健算法,，利用MUSIC算法和參數(shù)化估計(jì),，得到重構(gòu)的干擾噪聲協(xié)方差矩陣。其次,，使用了最大相關(guān)系數(shù)來估計(jì)出期望信號(hào)的SV,，該方法對(duì)于較大的干擾方向誤差有較好的穩(wěn)健性能。仿真結(jié)果表明：在采樣點(diǎn)較少或輸入SNR較低和較高時(shí),，該方法都存在一個(gè)最優(yōu)的輸出SINR,。

　　參考文獻(xiàn)

　　［1］ REED I S, MALLETT J D, BRENNAN L E. Rapid convergence rate in adaptive arrays［J］. IEEE Transactions on Aerospace & Electronic Systems, 1974, AES 10(6):853-863.

　?。?］ SHEN S, YU W, SINICA A, et al. Detection, estimation, and modulation theory［M］. Publishing House of Electronics Industry, 2003.

　?。?］ GU Y, LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation［J］. IEEE Transactions on Signal Processing, 2012, 60(7):3881-3885.

　　［4］ HUANG L, ZHANG J, XU X, et al. Robust adaptive beamforming with a novel interference plus noise covariance matrix reconstruction method［J］. IEEE Transactions on Signal Processing, 2015, 63(7):1643-1650.

　?。?］ CHEN F, SHEN F, SONG J. Robust adaptive beamforming using low complexity correlation coefficient calculation algorithms［J］. Electronics Letters, 2015, 51(6):443-445.

　?。?］ SANTOS E L, ZOLTOWSKI M D. Spatial power spectrum estimation based on a MVDR MMSE MUSIC hybrid beamformer［C］.IEEE International Conference on Acoustics, 2005:809-812.

　　［7］ SCHMIDT R O. Multiple emitter location and signal parameter estimation［J］. IEEE Transactions on Antennas & Propagation, 1986, 34(3):276-280.

　?。?］ LI J, STOICA P, WANG Z. On robust Capon beamforming and diagonal loading ［J］. IEEE Transactions on Signal Processing, 2003, 51(7):1702-1715.

　?。?］ JIA W, JIN W, ZHOU S, et al. Robust adaptive beamforming based on a new steering vector estimation algorithm ［J］. Signal Processing, 2013, 93(9):2539-2542.

　　［10］ VOROBYOV S, GERSHMAN A B, LUO Z Q. Robust adaptive beamforming using worst case performance optimization: a solution to the signal mismatch problem ［J］. IEEE Transactions on Signal Processing, 2003, 51(2):313-324.