0 引言

    余數(shù)系統(tǒng)作為一種數(shù)值表征系統(tǒng),，憑借其在并行計(jì)算,、數(shù)字信號(hào)處理以及大規(guī)模集成電路等領(lǐng)域的潛在應(yīng)用前景，受到了廣泛的研究,。近些年來(lái),，隨著冗余余數(shù)系統(tǒng)(Redundant Residue Number System，RRNS)及其相關(guān)算法在糾錯(cuò)領(lǐng)域的不斷應(yīng)用,，余數(shù)基的選擇和構(gòu)建變得愈發(fā)重要,。模乘單元的性能對(duì)于一種基的選擇和構(gòu)建起到了關(guān)鍵的作用，如何提供更多形式的高速模乘法器成為了余數(shù)系統(tǒng)發(fā)展的關(guān)鍵問(wèn)題之一,。

    2ⁿ-2^p±1形式的基可以構(gòu)建出高平衡度的余數(shù)基,，是RRNS中最常用的一種基。其對(duì)應(yīng)的乘法器也已經(jīng)被廣泛的研究,。在文獻(xiàn)[4]中,，一種通用形式的模乘法器被提出，雖然可以用來(lái)構(gòu)造模(2ⁿ-2^p-1)乘法器,，但是效果不佳,。在文獻(xiàn)[5]中，我們提出了一種剩余范圍的擴(kuò)展方法,，通過(guò)這種方法,，在沒(méi)有開(kāi)銷的情況下將剩余范圍從[0，2ⁿ-2^p-1]擴(kuò)展到[0,，2ⁿ-1],，為化簡(jiǎn)模(2ⁿ-2^p-1)乘法器的結(jié)構(gòu)提供了便利。在文獻(xiàn)[6,，7]中,，基于Booth編碼的模(2ⁿ-2^p-1)乘法器被提出，但是由于Booth編碼引入了負(fù)數(shù),，而負(fù)數(shù)在模乘法器中的修正問(wèn)題會(huì)造成較大的性能損失,。文獻(xiàn)[8]提出了一種高效且利于EDA實(shí)現(xiàn)的TDM壓縮樹(shù)(Three Dimensional Minimization，TDM)算法,?？紤]到余數(shù)系統(tǒng)中乘法器是無(wú)符號(hào)的且位數(shù)不高(通常小于32)，采用非Booth編碼的TDM壓縮樹(shù)結(jié)構(gòu)反而可以起到很好的效果。本文提出的模(2ⁿ-2^p-1)乘法器沿用了剩余范圍的擴(kuò)展方法,，采用TDM壓縮樹(shù)解決[6,，7]中出現(xiàn)的負(fù)數(shù)修正問(wèn)題，取得了較大的性能提升,。

    本文首先介紹TDM壓縮樹(shù)及剩余范圍的擴(kuò)展方法,，然后提出高速模(2ⁿ-2^p-1)乘法器的結(jié)構(gòu)并給出結(jié)構(gòu)圖，最后進(jìn)行分析對(duì)比,。

1 TDM壓縮樹(shù)算法

    在全加器中,，不同輸入端到不同輸出端的延遲是不同的。文獻(xiàn)[8]中提出TDM算法可以將壓縮樹(shù)中不同全加器的最長(zhǎng)延遲路徑和最短延遲路徑相連接,。這種算法可以很方便地用腳本實(shí)現(xiàn),，具有通用性。為了解決布局布線的不規(guī)整的問(wèn)題,，TDM算法支持將全加器替換為4：2或者其他形式的壓縮器,，以進(jìn)一步提升速度。最終通過(guò)TDM壓縮樹(shù)可以將部分積(Partial Product,，PP)壓縮至兩行。需要注意的是,，雖然相較文獻(xiàn)[6,，7]中采用的Booth編碼的混合型壓縮結(jié)構(gòu)，TDM壓縮樹(shù)會(huì)產(chǎn)生較大的面積,，但是考慮到Booth編碼引入負(fù)數(shù)所帶來(lái)的復(fù)雜修正問(wèn)題,，這些面積會(huì)被抵消且總的延遲更小。

2 剩余范圍的擴(kuò)展方法

3 高速模(2ⁿ-2^p-1)乘法器的結(jié)構(gòu)

    假設(shè)A[n-1:0]是乘數(shù),，B[n-1:0]是被乘數(shù),，A[n-1:0]×B[n-1:0]所產(chǎn)生的PP被TDM壓縮樹(shù)壓縮至兩列，分別為P₀[2n-2:0],，P₁[2n-2:0],。模(2ⁿ-2^p-1)乘法器可以被表示為：

    其中H₀[n-2:0]，L₀[n-1:0]分別代表P₀[2n-2:0]的高n-1位和低n位,。H₁[n-2:0],，L₁[n-1:0]分別代表P₁[2n-2:0]的高n-1位和低n位。根據(jù)文獻(xiàn)[5]中模(2ⁿ-2^p-1)乘法器的性質(zhì),，有：

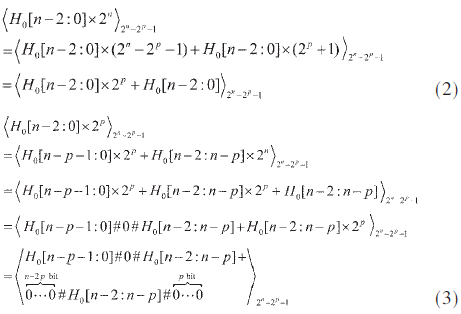
    其中符號(hào)#用來(lái)連接各比特位,。將式(2)、式(3)帶入式(1),，可以進(jìn)一步得到：

    將式(4)中前四項(xiàng)和后四項(xiàng)分別兩個(gè)(n-1)位的CSA和兩個(gè)n位的CSA進(jìn)行處理,，可以得到：

其中MH[n-1:0]，ML[n-1:0]為兩個(gè)(n-1)位的CSA的輸出,，NH[n:0],，NL[n:0]為兩個(gè)(n-1)位的CSA的輸出,。NH[n:0]和NL[n:0]可以進(jìn)一步折疊：

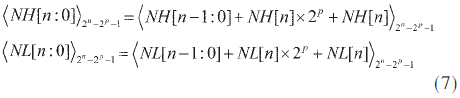
    將四個(gè)n位的部分項(xiàng)MH[n-1:0]，ML[n-1:0],，NH[n-1:0]以及ML[n-1:0]繼續(xù)用兩個(gè)n位CSA進(jìn)行處理,，得到：

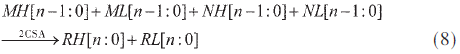
    其中RH[n:0]和RL[n:0]為這兩個(gè)n位CSA產(chǎn)生的輸出且可以繼續(xù)折疊：

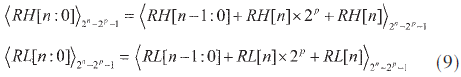
    令C[2:0]=NH[n]+NL[n]+RH[n]+RL[n]，式(9)產(chǎn)生的四個(gè)部分項(xiàng)可以進(jìn)一步用一個(gè)n位CSA壓縮：

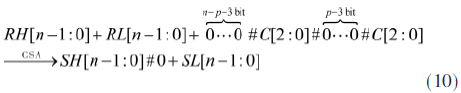
    將得到的SH[n-1:0]修正為：

    將SH[n-2:0]#SH[n-1]和SL[n-1:0]用一個(gè)n位二進(jìn)制加法器相加得到R[n:0]：

其中M=R[n]+SH[n-1],。實(shí)驗(yàn)證明當(dāng)n≥2p時(shí),，結(jié)果不會(huì)溢出。整體結(jié)構(gòu)如圖2所示,，在關(guān)鍵路徑上包含1個(gè)TDM壓縮樹(shù),，5個(gè)CSA，以及2個(gè)n位的二進(jìn)制加法器,。

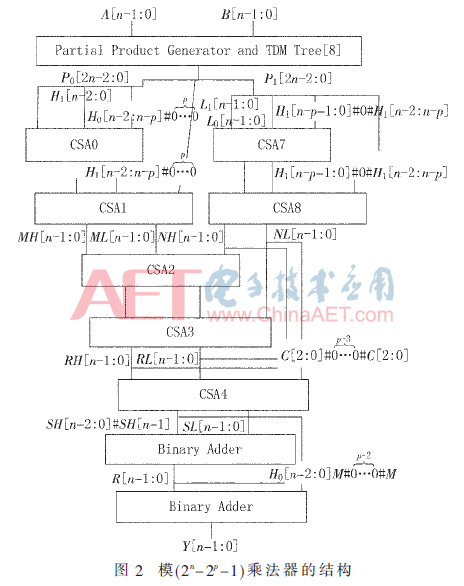
4 分析與比較

    我們將本文提出的模(2ⁿ-2^p-1)乘法器和文獻(xiàn)[4,，5，6,，7]中的模乘法器進(jìn)行對(duì)比分析,。所有的模乘法器都采用Verilog 硬件描述語(yǔ)言進(jìn)行建模，并采用Design Complier 在90 nm COMS工藝下進(jìn)行綜合,。

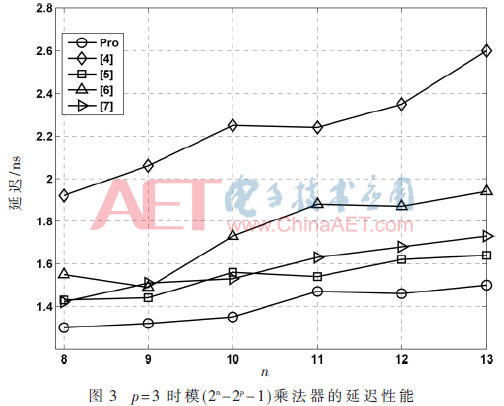
    綜合結(jié)果表明,，相較于文獻(xiàn)[4]中的設(shè)計(jì)，本設(shè)計(jì)的平均延遲降低49%,，平均面積降低了5.1%,。與文獻(xiàn)[5]中的設(shè)計(jì)相比，本設(shè)計(jì)的平均延遲降低了10.4%,，但是平均面積提升了4.5%,。和文獻(xiàn)[6]相比，本設(shè)計(jì)平均延遲降低了23.2%而平均面積降低了26.1%,。與文獻(xiàn)[7]進(jìn)行比較,，本設(shè)計(jì)平均延遲降低了10.3%，平均面積提升了1.3%,。

    文獻(xiàn)[5,，7]中的兩種設(shè)計(jì)是兩種典型的高效模(2ⁿ-2^p-1)乘法器，下面將著重對(duì)本設(shè)計(jì)以及文獻(xiàn)[5,，7]進(jìn)行靜態(tài)分析,。設(shè)計(jì)[5，7]都包含一個(gè)Booth 編碼的壓縮樹(shù),，而本設(shè)計(jì)包含一個(gè)非Booth的TDM壓縮樹(shù),，這兩種結(jié)構(gòu)的延遲相差不大。比較重點(diǎn)放在產(chǎn)生兩個(gè)2n-1位PP后的路徑，我們稱之為關(guān)鍵路徑,。文獻(xiàn)[5]的關(guān)鍵路徑包含1個(gè)2n位二進(jìn)制加法器,，1個(gè)CSA，3個(gè)n位二進(jìn)制加法器,。文獻(xiàn)[7]的關(guān)鍵路徑包含6個(gè)CSA和三個(gè)二進(jìn)制加法器,。與文獻(xiàn)[5]相比，本設(shè)計(jì)在關(guān)鍵路徑上使用四個(gè)CSA替代了一個(gè)2n位的大加法器和一個(gè)n位的小加法器,。與文獻(xiàn)[7]相比,，本設(shè)計(jì)在關(guān)鍵路徑上減少了一個(gè)CSA和一個(gè)2n位加法器。采用文獻(xiàn)[4]中的單位門評(píng)估方法,，具體結(jié)果如表1所示,。

5 結(jié)論

    得益于剩余范圍的擴(kuò)展和TDM壓縮樹(shù)的使用，本設(shè)計(jì)沒(méi)有使用復(fù)雜的模加法器且避免了負(fù)數(shù)修正問(wèn)題,。相較于當(dāng)前的模(2ⁿ-2^p-1)乘法器有較大的延遲性能提升,，是目前已知的延遲性能最佳的模(2ⁿ-2^p-1)乘法器。

參考文獻(xiàn)

[1] 馬上,，胡劍浩.余數(shù)系統(tǒng)在VLSI設(shè)計(jì)中的基本問(wèn)題研究與進(jìn)展[C].中國(guó)通信集成電路技術(shù)與應(yīng)用研討會(huì),，2006.

[2] 李磊，胡劍浩,，敖思遠(yuǎn).高速Booth編碼模(2^n—1)乘法器的設(shè)計(jì)[J].微電子學(xué)與計(jì)算機(jī),，2011，28(11)：191-193.

[3] 胡劍浩,，唐青.面向低電壓供電數(shù)字電路的容錯(cuò)計(jì)算系統(tǒng)結(jié)構(gòu)設(shè)計(jì)[J].電子科技大學(xué)學(xué)報(bào)，2013(6)：831-835.

[4] HIASAT A A.New efficient structure for a modular multiplier for RNS[J].IEEE Transactions on Computers,，2000,，49(2)：170-174.

[5] LI L，HU J,，CHEN Y.An universal architecture for designing modulo(2n-2p-1) multipliers[J].Ieice Electronics Express,，2012，9(3)：193-199.

[6] LI L,，LI S,，YANG P，et al.Booth encoding modulo(2n-2p-1) multipliers[J].Ieice Electronics Express,，2014,，11(15).

[7] YAN H，LI L,，ZHANG Q.A high speed modulo(2n-2p+1) multiplier design[J].Ieice Electronics Express,，2015，12(23).

[8] OKLOBDZIJA V G，VILLEGER D,，LIU S S.A method for speed optimized partial product reduction and generation of fast parallel multipliers using an algorithmic approach[J].IEEE Transactions on Computers,，1996，45(3)：294-306.