0 引言

　　對(duì)于無(wú)線網(wǎng)絡(luò),，與時(shí)間和頻率不同[1-2]，自適應(yīng)天線把空間作為一種新的資源,。為獲得以上參數(shù),，產(chǎn)生了幾何單反射信道模型(Geometrically-Based Single-Bounce Channel Models，GBSBCMs)的概念,，即假設(shè)單個(gè)散射體處于二維[3-6]或三維空間[7-9]中,。文獻(xiàn)[10]、文獻(xiàn)[11]分別計(jì)算了到達(dá)角度（Angle Of Arrival,，AOA)概率密度函數(shù)的大概形式和到達(dá)時(shí)延(Time Of Arrival,，TOA)概率密度函數(shù)的閉式表達(dá)式,，但它們只對(duì)散射體分布的小標(biāo)準(zhǔn)差有效,。為了避免遙遠(yuǎn)散射體的影響，只有低于一個(gè)給定閾值或者功率水平高于可接受值的散射體圓模型才被用于宏蜂窩,?？梢?jiàn)，在宏蜂窩中圓模型與橢圓模型結(jié)合比單獨(dú)的圓形散射體更合適,，因此需要研究更為一般的散射體模型,。

　　綜上所述，本文提出了更為一般的模型,，即圓形模型(Circular Model,，CM)和橢圓形模型(Elliptical Model，EM)的結(jié)合,，其適用于廣泛的無(wú)線蜂窩網(wǎng)絡(luò),。本文重點(diǎn)研究了散射體高斯分布下基站(Base Transceiver Station，BTS)接收信號(hào)AOA和到達(dá)路徑(Range of arrival,，ROA)的聯(lián)合概率密度函數(shù)和邊緣概率密度函數(shù),。

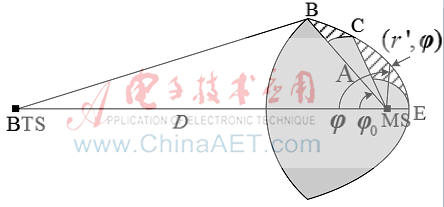
1 系統(tǒng)模型

　　如圖1，BTS位于坐標(biāo)原點(diǎn),，MS在X軸上,，MS相距BTS為D。

圖1  散射體模型

　　文中用到的符號(hào)見(jiàn)表1,。

　　由文獻(xiàn)[12]可知：

　　其中,，rb是r和的函數(shù)：

　　ROA/AOA聯(lián)合概率密度函數(shù)和為：

2 空間特性

　　2.1 ROA和AOA的聯(lián)合概率密度函數(shù)

　　在均勻散射體分布中，有：

　　其中，AU,、RA,，r分別表示概率質(zhì)量、公共區(qū)域,，且：

　　假設(shè)散射體從MS處呈鐘形增長(zhǎng),，則散射體的分布為：

　　因此ROA和AOA的聯(lián)合概率密度函數(shù)為：

　　其中，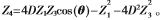

　　2.2 到達(dá)路徑（ROA）的概率密度函數(shù)

　　為了得到AG的閉式表達(dá)式：首先得到長(zhǎng)軸為r的橢圓與散射區(qū)域相交的部分的

　　當(dāng)散射體以高斯分布對(duì)稱地分布在圓形區(qū)域中時(shí),，總的概率質(zhì)量為：

　　其中在式（11）中,，一個(gè)角度為的扇形區(qū)域的概率質(zhì)量為：

　　由式(12)不僅可以得到的概率質(zhì)量，也可得到每個(gè)小區(qū)域的概率質(zhì)量,。如圖2(a)的不對(duì)稱區(qū)域的概率質(zhì)量不能直接計(jì)算,。當(dāng)r<<R且較小時(shí)，TOA的概率密度函數(shù)才符合蒙特卡羅模擬,。如圖2(b)將0等分成N個(gè)角(N要足夠大),。

(a)文獻(xiàn)[7]

(b)本文

圖2  ROA的累積分布函數(shù)

　　由式(12)可以計(jì)算扇區(qū)k的概率質(zhì)量為：

　　其中Vk是半徑為rk的圓圈的概率質(zhì)量：

　　A2的概率質(zhì)量是所有扇區(qū)概率質(zhì)量的總和，ROA的概率分布函數(shù)對(duì)r求導(dǎo)可以得到ROA的概率密度函數(shù)為：

　　其中,，且：

　　2.3 AOA的概率密度函數(shù)

　　由圖3可計(jì)算的值,。如圖4，其中,，由式(12)中可以得：

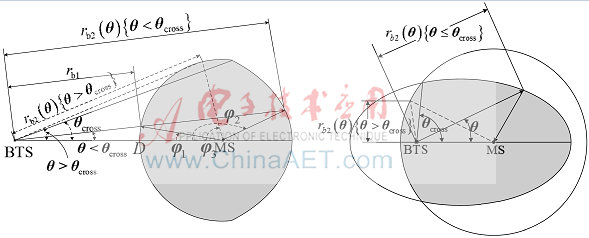
圖3  兩種情況下的rb1和rb2

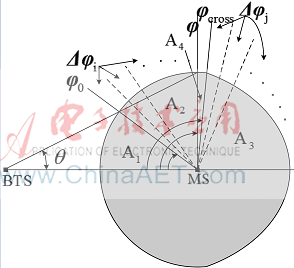
圖4  高斯散射體分布的AOA的累積分布函數(shù)

　　為了得到,，將角度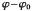等分成N1個(gè)角度：

　　是第i個(gè)扇區(qū)的概率質(zhì)量，第i個(gè)扇區(qū)的半徑ri：

　　同理有：

　　其中是第j個(gè)扇區(qū)的概率質(zhì)量,，rj是第j個(gè)扇區(qū)的半徑,，所以AOA的概率分布函數(shù)為：

　　因此AOA的概率密度函數(shù)為：

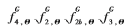　　同理可求得，有：

　　其中G1～G11的值可自行計(jì)算,。

3 數(shù)值結(jié)果與分析

　　如圖5描述了本模型散射體高斯分布下的ROA/AOA的聯(lián)合概率密度,。為不失一般性，文中定量給出信道模型選擇為標(bi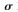āo)準(zhǔn)差=R/2,，R=500 m,，rm=1 800 m。由圖可知,，基站BTS接收信號(hào)基本是在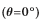小角度附近處,，而在大角度處其概率密度函數(shù)較小。研究發(fā)現(xiàn),，當(dāng)R<D,，再令rm=D+2R的情況下，ROA/AOA的聯(lián)合概率密度函數(shù)與文獻(xiàn)[11]中圓形散射體模型TOA/AOA的聯(lián)合概率密度相同,。相同地,，當(dāng)R≥D,、R=rm/2+D/2時(shí)，ROA/AOA的聯(lián)合概率密度函數(shù)與文獻(xiàn)[11]中橢圓形散射體模型TOA/AOA的聯(lián)合概率密度相同,。

圖5  高斯散射體分布的ROA和AOA的聯(lián)合概率密度函數(shù)

　　圖6描述的分別是散射體高斯分布下散射體模型的ROA概率密度函數(shù),。比較兩圖可以發(fā)現(xiàn)，在ROA為1 000 m~1 200 m的范圍內(nèi),，ROA的概率密度函數(shù)都會(huì)隨著ROA值的增大而急劇減小,，但當(dāng)ROA取值為1 500 m~2 000 m時(shí)，ROA的概率密度函數(shù)基本保持不變,。在文獻(xiàn)[12]中,，只有當(dāng)較小時(shí)，概率密度函數(shù)才符合蒙特卡羅模擬,。而本文獲得的概率密度函數(shù)對(duì)取任意值時(shí)蒙特卡羅模擬都是成立的,。

(a)一般模型

(b)圓形模型

圖6  高斯散射體ROA的概率密度函數(shù)

　　圖7描述的是散射體為高斯分布下一般模型和圓模型的AOA的概率密度函數(shù)。由圖可知,，角度=0°附近AOA的概率密度函數(shù)有最大值,，在=0°兩側(cè)呈對(duì)稱性衰減。隨著角度的增大(或減小),，AOA的概率密度函數(shù)逐漸減小為零,。在文獻(xiàn)[12]中，只有當(dāng)?滓較小時(shí),，概率密度函數(shù)才符合蒙特卡羅模擬,。而本文得到的概率密度函數(shù)對(duì)于任意的值都是符合蒙特卡羅模擬的,。

(a)一般模型

(b)圓形模型

圖7  高斯分布散射體的AOA的概率密度函數(shù)

4 結(jié)語(yǔ)

　　本文研究了基于二維空間域統(tǒng)計(jì)信道模型的空時(shí)參數(shù),，提出了更為一般的CM與EM模型結(jié)合的改進(jìn)型空間衰落信道模型。在散射體高斯分布的情況下,，分別導(dǎo)出了BTS接收信號(hào)AOA/ROA的聯(lián)合概率密度函數(shù)和邊緣概率密度函數(shù),，揭示了無(wú)線環(huán)境下基站BTS端的到達(dá)角度以及到達(dá)路徑的特性。分析結(jié)果顯示本模型的應(yīng)用研究符合蒙特卡羅模擬,，為評(píng)估幾何單反射信道模型在無(wú)線環(huán)境中的多徑衰落信道參數(shù)提供了更為一般的散射體模型,，適用范圍更廣，進(jìn)一步擴(kuò)展了二維空間信域模型的研究與分析,。

　　參考文獻(xiàn)

　　[1] LIBERTI J,，RAPPAPORT T S.Smart antennas for wirless communications：IS-95 and third generations CDMA applications[M].Prentice Hall PTR，1999.

　　[2] WIDROW B,，MANTEY P E,，GRIFFITHS，et al.Adaptive antenna systems[J].IEEE,，1967,，55(12)：2143-2159.

　　[3] LIBERTI J C,，RAPPAPORT T S.A geometrically based model for line-of-sight multipath radio channels[C].IEEE Vehicular Technology Conference，1996,，2：844-848.

　　[4] BORHANI A,，PATZOLD M.Aunified disk scattering model andits angle-of-departure and time-of-arrival statistics[J].IEEE Transactions on Vehicular Technology，2013,，62(2)：473-485.

　　[5] GUO L,，NIAN X.TOA and AOA statistics for distant circular scattering model[J].Journal of Electrical Engineering，2012,，10(3)：564-571.

　　[6] MAMMASIS K,，SANTI P.A two-dimensional geometrybased stochastic model[J].IEEE Transactions on Wireless Communications，2012,，11(1)：38-43.

　　[7] KARADIMAS P,，ZHANG J.A generalized analysis of threedimentional anisotropic scattering in mobile wireless channels part I：Theory[C].IEEE 73rd Vehicular Technology Conference，2011：1-5.

　　[8] ZHU X,，WANG Y,，ZHU X，et al.Angle of arrival statistics for a 3-D cylinder model[J].Wireless Personal Communications,，2012,，64(6)：847-857.

　　[9] NWAZ S J，QURESHI,，KHAN N M.A generalized 3-D scattering model for a macrocell environment with a directional antenna at the BS[J].IEEE Transactions on Venhicular Technology,，2010，59(7)：3193-3204.

　　[10] JANASWAMY R.Angle and time of arrival statistics for the Gaussian scatter density model[J].IEEE Transactions on Wireless Communications,，2002,，1(3)：488-497.

　　[11] KONG S H.TOA and AOA statistics for down link Gaussian scatterer distribution model[J].IEEE Transactions on Wireless Communications，2009,，8(5)：2609-2617.

　　[12] PAPOULIS A.Probability,，random variables, and stochastic processed[M].3rd ed，New York：McGraw-Hill,，1991.