謝玲1,2

　?。?.南京理工大學 紫金學院,，江蘇 南京 210046；2.南京大學 計算機科學與技術系,，江蘇 南京 210000）

　　摘要：BB84協(xié)議是目前最接近實用化的量子密鑰分發(fā)（QKD）協(xié)議,。點對點的量子密鑰分發(fā)系統(tǒng)已經可以商用，但現(xiàn)有的多用戶量子密鑰分發(fā)協(xié)議都是采用量子糾纏,、量子存儲等技術手段進行密鑰分發(fā),，在現(xiàn)有的技術條件下只能停留在理論階段，離工程應用還有較長的距離,。該文提出了一種基于BB84的多用戶量子密鑰分發(fā)協(xié)議,，將計算機通信技術應用到量子保密通信中，實現(xiàn)一對多的量子通信網絡的量子密鑰分發(fā),，并從理論和實驗結果兩方面分析其可行性,。

　　關鍵詞：量子保密通信；量子密鑰分配,；多用戶,；BB84

0引言

　　當今世界，信息的安全至關重要,，信息安全中最核心的技術是經典密碼技術,。自從Peter Shor在1994年提出了第一個具體的量子算法［1］，RSA等基于大數(shù)質因子分解難題的公鑰密碼系統(tǒng)的安全性面臨前所未有的挑戰(zhàn),。量子保密通信特別是量子密鑰分發(fā)技術(QKD)近年來得到了快速發(fā)展,。

　　世界上第一個量子保密通信協(xié)議是BB84協(xié)議［2］，由BENNETT C H和BRASSARD G在1984年提出。該協(xié)議使得經過認證的通信雙方在兩地能夠連續(xù)建立密鑰,，進而通過OTP（一次一密亂碼本）加密協(xié)議實現(xiàn)安全通信,。BB84協(xié)議與經典密碼體系中的基于計算復雜性的基本原理不同，它是以量子力學為基礎,，以“海森堡測不準原理”和“量子態(tài)不可精確克隆”這兩個性質為原理,，在歷史上第一次提供了無條件安全性的方法，開辟了密鑰分發(fā)和保密通信的新方向,。BB84協(xié)議簡單,，可操作性強，其提出之后的20多年里,，人們逐步完成了包括理想情況和各種現(xiàn)實條件下的安全性證明［310］,，進行了實驗室的演示以及現(xiàn)有光纖和自由空間條件下的一系列工作。

　　然而,，BB84協(xié)議雖然可以保證點對點通信雙方獲得安全密鑰,，但對于一對多的多用戶通信來說，BB84協(xié)議適用性欠缺,。原因在于BB84協(xié)議在通信過程中隨機產生密鑰串,，導致接收端收到的密鑰各不相同，隨之而來的加密和解密的次數(shù)等同于接收端的數(shù)量,。近年來,，多用戶QKD協(xié)議（MUQKD）得到了發(fā)展［11-17］。然而,，這些MUQKD協(xié)議采用的技術手段如BELL基測量,、量子存儲和量子幺正變換，在現(xiàn)有的技術條件下只能停留在理論階段,，離工程應用還有較長的距離,。

　　本文提出了一種多用戶量子密鑰分發(fā)協(xié)議，將計算機通信與量子通信理論相結合,，在一對多的量子通信網絡中,，通信一次使接收端得到相互一致的密鑰，從而使發(fā)送端只需對信息進行一次加密,，即可將密文統(tǒng)一傳送至各接收端,。雙方的密鑰是在發(fā)送端產生的隨機比特，采用BB84協(xié)議傳輸密鑰,，保證了密鑰的安全性,，且大大減少了發(fā)送端的加密次數(shù)。采用計算機仿真驗證了該協(xié)議的可行性,，使發(fā)展高速量子通信網絡成為可能,。

1BB84量子通信協(xié)議

　　BB84不僅是目前最接近實用化的量子通信協(xié)議,，而且也是其他量子通信協(xié)議的基礎。該協(xié)議描述如何利用光子的偏振態(tài)來傳輸信息進行量子密鑰分發(fā)：發(fā)送方Alice和接收方Bob用量子信道(如果光子作為量子態(tài)載體,，對應的量子信道就是傳輸光子的光纖)來傳輸量子態(tài)；同時雙方通過一條公共經典信道(如因特網)比較測量基矢和其他信息交流,，進而兩邊同時安全地獲得或共享一份相同的密鑰,。公共信道的安全性不需考慮，BB84協(xié)議在設計時已考慮到了兩種信道都被第三方 (Eavesdropper,通常稱為Eve)竊聽的可能,。具體過程如下：

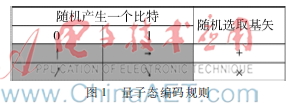
　?。?）Alice隨機產生一個比特0或比特1，并且隨機選取一對正交態(tài)基矢：“＋”基或“×”基,，從而將該光子制備成一個隨機的量子偏振態(tài),，其中，0°偏振態(tài)記作|→>,，90°偏振態(tài)記作|↑>,，+45°偏振態(tài)記作|↗>，-45°偏振態(tài)記作|↘>,。編碼情況如圖1所示,。

　　（2）Alice把制備在某個偏振態(tài)的光子通過量子信道傳送給Bob,，Bob接收到后開始測量該光子的量子態(tài),。測量時Bob并不知道Alice在制備量子態(tài)時選擇了哪個基矢，只能隨機選擇一個測量基矢（“＋”基或“×”基）來測量,。測量過程中,，Bob要記錄對接收到的每個光子所選的基以及測量結果。

　?。?）Alice通過公共經典信號公布制備每個光子偏振態(tài)時所選擇的基矢,，Bob將測量對應光子時所選擇的測量基矢與之進行對比，舍棄那些雙方選擇了不同基矢的比特（50%）,，剩下的比特還原并進行保存,，從而完成密鑰分發(fā)。此過程將有約一半的數(shù)據(jù)被篩選出來,，留下的密鑰稱為原始密鑰,。原始密鑰的形成過程如圖2所示?！?/p>

　?。?）雙方隨機公開一部分原始密鑰用來估計誤碼率，并判斷有沒有竊聽者Eve的存在,。對于竊聽者Eve來說,，如果選擇“＋”基來測量|↑>，會以100%的概率得到|↑>，但是如果用“＋”基來測量|↗>或|↘>態(tài)光子,，結果就是隨機的,，會以50%的概率得到|→>或|↑>。也就是說,，即使Eve選擇的測量基與Alice的一樣,，都是“＋”基，也無法分辨該光子原來的量子態(tài)是|↑>還是|↗>或|↘>(無法通過測量來徹底分辨非正交態(tài)),。然而一旦Eve對光子作了測量,，就不可能完全克隆出原來被截獲的光子。所以Eve的介入必然會額外增大錯誤率,。若誤碼率在一定的閾值范圍內,，可以通過糾錯技術進行糾錯，然后對糾錯后的密鑰進行隱私放大,，消除前面通信過程和糾錯過程中導致的信息泄露,，從而提取到無條件安全的密鑰；若誤碼率超過一定的閾值,，則放棄此次通信,，通信雙方選擇新的量子信道進行量子密鑰分發(fā)。

2基于BB84的多用戶量子密鑰分發(fā)協(xié)議

　　基于BB84的多用戶量子密鑰分發(fā)協(xié)議是針對一對多的量子密鑰分發(fā),。如圖3所示,，假如有1個發(fā)送端，4個接收端,，如果使用BB84協(xié)議,，密鑰分發(fā)過程需要4次，每次產生的密鑰各不相同,，所以發(fā)送端需要將信息分別加密4次,，再將所得的密文分別傳送至各個接收端。

　　在此基礎上本文提出了多用戶量子密鑰分發(fā)協(xié)議,。該協(xié)議工作過程如下：

　?。?）發(fā)送端隨機產生n位二進制密鑰串；

　?。?）將該密鑰串重復m次得到N位密鑰串,；

　　（3）發(fā)送端隨機選擇基矢,，將N位密鑰串制備成相應的量子偏振態(tài),，然后經由量子信道進行傳輸；

　?。?）接收端隨機選擇測量基對接收到的量子態(tài)進行測量,；

　?。?）雙方通過經典信道進行基矢比對，保留基矢相同的部分,，并告知發(fā)送端分組密鑰長度n,；

　　（6）基矢相同部分的量子態(tài)譯碼成相應的二進制比特,，然后將每組（一共m組）保留下來的二進制比特按位進行拼接,，得到一組與發(fā)送端相同的n位二進制密鑰串。

　?。?）對多個用戶進行密鑰分發(fā)時重復上述過程,，但n保持固定,。如此完成一次量子密鑰的分發(fā),。

　　采用此種協(xié)議的優(yōu)勢在于：

　　（1）經過一次多用戶的量子密鑰分發(fā),，發(fā)送端和多個接收端獲得的密鑰一致,，發(fā)送端只需加密一次，即可將密文發(fā)送至各接收端,，接收端規(guī)模越大,，此優(yōu)勢越明顯。

　?。?）一次多用戶量子密鑰分發(fā)過程產生的密鑰是隨機的,，發(fā)送端和接收端隨機選擇制備基矢和測量基矢，保證了傳輸?shù)陌踩?，當有竊聽者存在時,，誤碼率會增大，若誤碼率超過一定閾值,，則放棄此次通信,。

　　（3）在沒有竊聽者的理想情況下,，經過基矢比對篩選后,，通信雙方的原始密鑰應該是完全一致的。但是在現(xiàn)實系統(tǒng)中,，由于非理想的物理器件和非完美的物理信道傳輸,會導致接收方的原始密鑰有一定的誤差,，若誤碼率在一定的閾值范圍內，則在接收端進行密鑰拼接時按照少數(shù)服從多數(shù)的原則,，可將每段中的錯誤信息剔除,，最終得到與發(fā)送端一致的密鑰串。

　?。?）分組密鑰長度n和分組數(shù)m可根據(jù)接收端數(shù)據(jù)以及要加密的明文長度進行調節(jié),。

3理論和實驗結果

　　3.1理論分析

　　對于分組密鑰長度n和分組數(shù)m,，設得到最終密鑰的概率為p，計算可得：

　　當密鑰長度固定時,，可通過此公式選擇合適的分組數(shù)m,，使得p滿足不等式：P>P0,其中，P0為得到一致密鑰的最低閾值,，保證各通信終端以極高的概率獲取一致密鑰,。

　　3.2實驗分析

　　對m和n取不同的值進行實驗，統(tǒng)計密鑰獲得成功的概率,。實驗平臺如圖4所示,。　　

　　其中,，隨機碼位數(shù)為n,，分組數(shù)為m，實驗次數(shù)為接收端個數(shù),。

　　中間過程為模擬BB84工作過程,，如圖5所示。

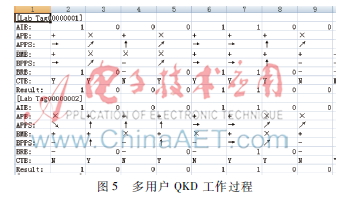
　　圖5中,，各參數(shù)意義如下：AIB為Alice生成的二進制隨機比特,；APB為Alice選擇的基矢；APPS為Alice的量子偏振態(tài),；BMB為Bob的測量基,；BPPS為Bob的量子偏振態(tài)；BRB為Bob接收的量子比特,；CTB為對基結果,，相同基為Y，否則為N,；Result為拼接結果,。

　　實驗如下：

　　（1）取n=8,，m為1~15,，接收端數(shù)目為10 000，實驗統(tǒng)計數(shù)據(jù)如圖6所示,。

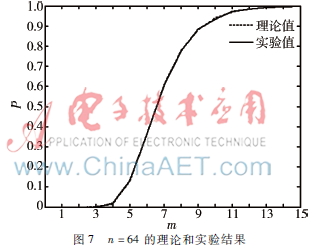
　?。?）取n=64，m為1~15,，接收端數(shù)目為10 000,，實驗統(tǒng)計數(shù)據(jù)如圖7所示。

　?。?）取n=128,，m為1~15,，接收端數(shù)目為10 000，實驗統(tǒng)計數(shù)據(jù)如圖8所示,。

4結論

　　上述實驗當分組數(shù)達到一定值時,，即可以較大的概率得到一致密鑰。而當分組數(shù)繼續(xù)增大時,，效果會變得不明顯,，且冗余信息較多。所以選擇合適的分組數(shù)非常重要,。

　　目前,，量子保密通信尤其是量子密鑰分發(fā)技術已成為具有重要戰(zhàn)略意義的前沿技術之一，本文提出了一種基于BB84的多用戶量子密鑰分發(fā)協(xié)議,，完成一對多通信網絡的量子密鑰分發(fā),，并用理論和仿真實驗分析了其可行性。

參考文獻

　?。?］ SHOR P W. Algorithms for quantum computation: discrete logarithms and factoring［C］. Foundations of Computer Science, 1994 Proceedings, 35th Annual Symposium on. IEEE, 1994:124134.

　?。?］ BENNETT C H, BRASSARD G. Quantum cryptography: public key distribution and coin tossing［C］. International Conference on Computer System and Signal Processing, IEEE,， 1984:175179.

　?。?］ SHOR P W, PRESKILL J. Simple proof of security of the BB84 quantum key distribution protocol［J］. Physical Review Letters, 2000, 85(2):441444.

　　［4］ SCARANI V, BECHMANNPASQUINUCCI H, CERF N J, et al. The security of practical quantum key distribution［J］. Reviews of Modern Physics, 2009, 81(10): 13011350.

　?。?］ LO H K, CHAU H F. Unconditional security of quantum key distribution over arbitrarily long distances［J］. Science, 1998, 283(5410): 20502056.

　?。?］ MAYERS D. Unconditional security in quantum cryptography［J］. Journal of the ACM(JACM), 2001, 48(3): 351406.

　　［7］ GOTTESMAN D, LO H K. Proof of security of quantum key distribution with twoway classical communications［J］. Information Theory, IEEE Transactions on, 2003, 49(2): 457475.

　?。?］ RENNER R. Security of quantum key distribution［J］. International Journal of Quantum Information, 2005, 6(1): 1127.

　?。?］ GOTTESMAN D, Lo H K, LTKENHAUS N, et al. Security of quantum key distribution with imperfect devices［J］. Quantum Information & Computation, 2002, 4(5):325360.

　　［10］ KOASHI M, PRESKILL J. Secure quantum key distribution with an uncharacterized source［J］. Physical Review Letters, 2003, 90(5): 057902.

　?。?1］ Li Chunyan, Zhou Hongyu, Wang Yan, et al. Secure quantum key distribution network with Bell states and local unitary operations［J］. Chinese Physics Letters, 2005, 22(5): 10491052.

　?。?2］ Li Chunyan, Li Xihan, Deng Fuguo, et al. Efficient quantum cryptography network without entanglement and quantum memory［J］. Chinese Physics Letters, 2006, 23(11): 28962899.

　　［13］ Deng Fuguo, Liu Xiaoshu, Ma Yingjun, et al. A theoretical scheme for multiuser quantum key distribution with N EinsteinPodolskyRosen pairs on a passive optical network［J］. Chinese physics letters, 2002, 19(7): 893896.

　?。?4］ Lin Song, Huang Chuan, Liu Xiaofen. Multiuser quantum key distribution based on Bellstates with mutual authentication［J］. Physica Scripta, 2013, 87(3): 035008.

　?。?5］ PHOENIX S J D, BARNETT S M, TOWNSEND P D, et al. Multiuser quantum cryptography on optical networks［J］. Journal of Modern Optics, 1995, 42(6): 11551163.

　　［16］ BIHAM E, HUTTNER B, MOR T. Quantum cryptographic network based on quantum memories［J］. Physical Review A, 1996, 54(4): 26512658.

　?。?7］ XUE P, LI C F, GUO G C. Conditional efficient multiuser quantum cryptography network［J］. Physical Review A, 2002, 65(2): 130132.