邵靖凱,厲旭杰
(溫州大學(xué) 物理與電子信息工程學(xué)院,浙江 溫州 325035)
摘要:提出了基于CUDA的并行拉普拉斯金字塔算法。算法采用的并行拉普拉斯算法很好地解決了共享存儲(chǔ)器的bank沖突和全局存儲(chǔ)器的合并訪問(wèn)的問(wèn)題,為了最大化并行效率,計(jì)算了SM占用率,并通過(guò)公式進(jìn)行了論證。在GTX480平臺(tái)下,基于CUDA的并行拉普拉斯金字塔算法獲得了幾十倍的加速比。最后,將基于CUDA的并行拉普拉斯金字塔算法成功地應(yīng)用于圖像融合和增強(qiáng)圖片的細(xì)節(jié)處理,充分證明了并行拉普拉斯金字塔算法廣泛的有效性和必要性。
關(guān)鍵詞:CUDA;拉普拉斯金字塔;GPU;并行計(jì)算
0引言
拉普拉斯金字塔算法可以進(jìn)行多尺度的圖像分解,廣泛應(yīng)用于圖像分析[12]。PARIS S等人[3]用拉普拉斯金字塔算法實(shí)現(xiàn)了邊緣突出的圖像處理,但是算法的效率很低。因此又提出限制拉普拉斯分解的層數(shù)的算法,從而提高圖像處理的速度,但是圖像處理的效果有所下降。雖然拉普拉斯金字塔分解本身算法復(fù)雜度不高,但是因?yàn)閼?yīng)用中通常需要進(jìn)行很多層的拉普拉斯分解和重構(gòu),使得整個(gè)過(guò)程需要消耗大量的時(shí)間。因此提高拉普拉斯金字塔算法的速度顯得非常重要。祁艷杰[4]實(shí)現(xiàn)了基于FPGA的實(shí)時(shí)拉普拉斯金字塔。
本文研究了基于CUDA的拉普拉斯金字塔算法的實(shí)現(xiàn)。本算法采用并行拉普拉斯算法很好地解決了共享存儲(chǔ)器的bank沖突和全局存儲(chǔ)器的合并訪問(wèn)的問(wèn)題,而且最大化了并行效率,從而使性能得到了很大的提高。
1圖像金字塔
1.1高斯金字塔的構(gòu)建過(guò)程
設(shè)原圖像為G0,高斯金字塔的第L層的構(gòu)造方法如下:先將L-1層圖像GL-1和窗口函數(shù)w(m,n)進(jìn)行卷積,結(jié)果做隔行隔列的降采樣,即
GL(i,j)=∑2m=-2∑2n=-2w(m,n)GL-1(2i+m,2j+n) (1)
其中,(i,j)為像素索引,w(m,n)是5×5高斯核:
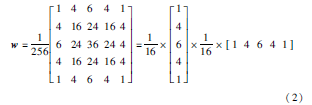
計(jì)算G0,G1,…,GN就構(gòu)成了高斯金字塔。
1.2拉普拉斯金字塔的構(gòu)建過(guò)程
將GL內(nèi)插放大,得到放大圖像G*L,使G*L的尺寸與GL-1的尺寸相同:
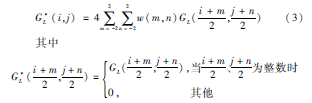
令LPL=GL-G*L+1,當(dāng)0≤L<N時(shí)
LPL=GL,當(dāng)L=N時(shí),則LP0,LP1,…,LPN構(gòu)成了拉普拉斯金字塔。
2基于CUDA的拉普拉斯金字塔的并行化實(shí)現(xiàn)
本文主要介紹基于CUDA的可分離高斯濾波器的實(shí)現(xiàn)。

從公式(5)中可以看出,高斯濾波器很適合在GPU上進(jìn)行高效的并行計(jì)算。公式(2)說(shuō)明,采用可分離濾波器可以分解成兩個(gè)一維高斯濾波器,可以使計(jì)算更加簡(jiǎn)單。
從圖1中可以看出,基于CUDA的拉普金字塔首先采用高斯卷積,然后下采樣得到高斯金字塔,高斯金字塔經(jīng)過(guò)上采樣,并經(jīng)過(guò)高斯卷積得到拉普拉斯金字塔。

對(duì)于圖像的卷積,通常的方法是將圖像的像素傳輸?shù)絞lobal memory,然后每個(gè)thread負(fù)責(zé)計(jì)算一個(gè)像素的卷積結(jié)果。然而這種方法需要大量訪問(wèn)全局寄存器,導(dǎo)致性能下降,甚至運(yùn)行的速度會(huì)比在CPU上的性能還要差。共享存儲(chǔ)器位于GPU片內(nèi),速度比表1所示使用CUDA profiler測(cè)試程序基于CUDA的可分離高斯金字塔local/global memory快得多。在不發(fā)生bank conflict的情況下,share memory的延遲幾乎只有l(wèi)ocal或global memory的1/100,訪問(wèn)速度與寄存器相當(dāng),是實(shí)現(xiàn)線程間通信延遲最小的方法。
為了減少空閑的線程和充分利用共享存儲(chǔ)器,本設(shè)計(jì)讓每個(gè)thread負(fù)責(zé)將多個(gè)全局寄存器數(shù)據(jù)傳輸?shù)焦蚕泶鎯?chǔ)器,負(fù)責(zé)多個(gè)像素的卷積,block尺寸為16×8,每個(gè)thread負(fù)責(zé)傳輸(2+8)個(gè)全局存儲(chǔ)器到共享存儲(chǔ)器,同時(shí)負(fù)責(zé)8個(gè)像素的卷積計(jì)算。設(shè)置Apron的寬度為16的倍數(shù),以便在存取全局存儲(chǔ)器時(shí)符合合并訪問(wèn)的條件。計(jì)算16×8×4像素的卷積,只需要用16×10×4的共享存儲(chǔ)器,有效利用了共享存儲(chǔ)器。
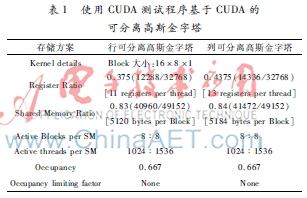
表1顯示了使用CUDA profiler測(cè)試程序基于CUDA的可分離高斯金字塔,其中行可分離高斯金字塔,每個(gè)線程用了11個(gè)寄存器,每個(gè)block使用了5 120 B的共享存儲(chǔ)器。而每個(gè)SM最多可激活8個(gè)block,通過(guò)下面的公式可以計(jì)算得到寄存器和共享存儲(chǔ)器的使用率。
塊內(nèi)總束數(shù)量Wblock如下[5]:
Wblock=ceil(T/Wsize,1)(5)
其中,T是塊內(nèi)線程數(shù),Wsize是束尺寸,ceil(x,y)等于x向上取到y(tǒng)的整數(shù)倍。
分給一個(gè)塊的總寄存器數(shù)量Rblock如下:
Rblock=ceil(Rk×Wsize,GT)×Wblock(6)
Rk是內(nèi)核使用的寄存器數(shù),GT是線程分配的粒度。
塊內(nèi)總共享存儲(chǔ)器數(shù)量Sblock如下:
Sblock=ceil(Sk,GS)(7)
其中,Sk是內(nèi)核使用的共享存儲(chǔ)器總量,以字節(jié)為單位,GS是共享存儲(chǔ)器分配的粒度。
通過(guò)公式(5)~(7)可以計(jì)算得到寄存器和共享存儲(chǔ)器的使用率,為了選取合適的block大小,提高SM占用率,通過(guò)CUDA GPU Occupancy Calculator來(lái)選擇block的大小,從圖2中可以看出,選取block圖2使用CUDA GPU Occupancy Calculator計(jì)算block大小、寄存器大小和共享存儲(chǔ)器的使用對(duì)SM占用率的影響大小為16×8×1可以使SM占用率提高到0.667,這個(gè)結(jié)果與用CUDA profiler測(cè)試的結(jié)果和公式(5)~(7)計(jì)算的結(jié)果是一致的。如果繼續(xù)增加block的大小,從表1或者公式(5)~(7)都很容易得到,因?yàn)楣蚕泶鎯?chǔ)器容量的限制,SM占用率不會(huì)因?yàn)閎lock大小的增加而增加,而選擇block大小為16×4×1,SM占用率為0.33。因此在GTX480上,選取Block大小為16×8×1是最合適的。

3實(shí)驗(yàn)結(jié)果
3.1性能測(cè)試
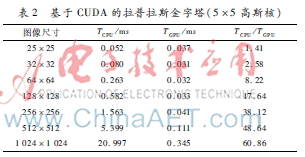
表2顯示了基于CUDA的拉普拉斯金字塔性能的測(cè)試結(jié)果。結(jié)果顯示提出的算法獲得了幾十倍的加速比。基于CUDA的拉普拉斯金字塔采用可分離卷積濾波核,很好地解決了利用了共享存儲(chǔ)器和全局存儲(chǔ)器的合并訪問(wèn)的要求。
3.2拉普拉斯金字塔的應(yīng)用
(1)基于拉普拉斯金字塔的融合

圖3金字塔變換后區(qū)域特征量測(cè)所得圖像(3層拉普拉斯金字塔分解)采用基于區(qū)域特征量測(cè)的拉普拉斯金字塔分解的圖像融合算法,圖3顯示了金字塔變換后區(qū)域特征量測(cè)所得圖像(3層拉普拉斯金字塔分解)。當(dāng)層數(shù)較低時(shí),如分解層數(shù)小于5層,分解層數(shù)越大,融合圖像的分辨率越高,圖像越清晰;當(dāng)層數(shù)大于5層時(shí),增加層數(shù)對(duì)于改善分辨率的影響減小,但增大了計(jì)算量。而基于CUDA的拉普拉斯金字塔由于性能上有較大的提高,可以支持層數(shù)大于5層的實(shí)時(shí)圖像融合。因此基于CUDA的拉普拉斯金字塔特別適合對(duì)圖像融合效果要求高而需要進(jìn)行很多層拉普拉斯金字塔分解的實(shí)時(shí)圖像融合。
(2)基于拉普拉斯金字塔的增強(qiáng)圖片的細(xì)節(jié)處理,PARIS S等人[4]用拉普拉斯金字塔算法在處理圖像平滑、圖像細(xì)節(jié)控制、色調(diào)映射等領(lǐng)域表現(xiàn)出了很好的特性,不足之處是每處理一萬(wàn)個(gè)像素需要近1 min時(shí)間,圖4顯示了圖像邊緣保持的細(xì)節(jié)提高,在圖6中圖像尺寸為300×200的情況下,需要進(jìn)行8次拉普拉斯分解和重構(gòu),整個(gè)程序需要耗時(shí)3 min。而基于CUDA的拉普拉斯金字塔算法在GTX480平臺(tái)下獲得了幾十倍的加速比。

4結(jié)語(yǔ)
本文提出了基于CUDA的并行拉普拉斯金字塔算法,二維高斯濾波被分解成可分離的兩個(gè)一維卷積操作。提出的基于CUDA的拉普拉斯金字塔算法在GTX480平臺(tái)下獲得了幾十倍的加速比。
參考文獻(xiàn)
[1] 趙健,高軍,羅超,等. 基于數(shù)字圖像處理的玻璃缺陷在線檢測(cè)系統(tǒng)[J]. 電子技術(shù)應(yīng)用, 2013,39(12):9092.
[2] 李波,梁攀,關(guān)沫. 一種基于邊緣提取的交互式圖像分割算法[J]. 微型機(jī)與應(yīng)用, 2013, 32(10):4147.
[3] PARIS S, HASINOFF S, KAUTZ J. Local Laplacian filters: edgeaware image processing with a Laplacian pyramid[J]. ACM Transactions on Graphics, 2011,30(4):12441259.
[4] 祁艷杰. LOG算子在FPGA中的實(shí)現(xiàn)[J]. 電子技術(shù)應(yīng)用, 2007, 33(3):6365.
[5] NVIDIA. NVIDIA CUDA programming guide 4.0[EB/OL].(201132)[20160329]http://developer.nvidia.com/cudatoolkit40.

