王 成,，劉 坤,，丁祖萍

　　（上海海事大學 信息工程學院,，上海 201306）

　　摘  要： 像素級圖像融合需要對待融合圖像的像素灰度進行綜合分析與處理,，而巨大的數(shù)據(jù)量給圖像融合帶來了極大的不便。壓縮感知理論的興起提供了一種新的數(shù)據(jù)采集和壓縮方法,，它利用圖像的部分信息重構原始圖像,，有效減輕了圖像處理的計算復雜度。本文基于對壓縮感知理論的研究,，把壓縮感知的方法應用于圖像融合,，并嘗試通過對壓縮感知觀測矩陣的改進提高融合質(zhì)量。文中設計出一種適應于DCT域的射線采樣矩陣,，通過與隨機生成的觀測矩陣融合效果的比較,，證明該方法取得了良好的融合效果,。

　　關鍵詞： CS理論；圖像融合,；DCT稀疏,；射線采樣矩陣

0 引言

　　近年來信息技術的飛速發(fā)展使得人們對信息的需求量急劇增加，傳統(tǒng)的以奈奎斯特采樣定理為根本采樣方法的模式極大地阻礙了人們對信息的獲取,。壓縮感知理論[1-3]（Compressed Sensing,，CS）是由Donoho、Candes和Romberg等人于2006年正式提出的一種新穎的數(shù)據(jù)采樣理論,。與此同時,，Candes等人也為該理論的提出做了大量的基礎研究工作。壓縮感知的方法利用變換空間描述信號,，并直接采集得到少數(shù)“非常重要”的線性觀測數(shù)據(jù),，最后通過求解一個優(yōu)化問題就可以從壓縮觀測獲得的數(shù)據(jù)中恢復原始信號。

　　基于此,，將壓縮感知的觀點引入到圖像融合[4]可以有效解決圖像融合中需要處理巨大數(shù)據(jù)量的問題,。基于壓縮感知方法的圖像融合是將融合規(guī)則應用于經(jīng)過壓縮而產(chǎn)生的測量值,，將源圖像的主要信息提取出來進行融合得到融合圖像,。在壓縮感知的整個過程中，觀測矩陣的選擇對于數(shù)據(jù)采樣有著至關重要的影響,。本文把壓縮感知的方法應用到圖像融合的過程中,，著重研究了測量矩陣對融合圖像質(zhì)量的影響，并構造出一種適用于特定稀疏域的觀測矩陣,。實驗結果表明,，該方法取得了良好的融合效果。

1 壓縮感知的基本理論

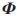　　壓縮感知是把一維信號x∈RN×l在一組稀疏基={1,，…,，N}下稀疏表示，即： ,。然后構造一個與?鬃不相關的觀測矩陣M×N對信號x進行一個壓縮觀測：y=x,，由此得到M個線性觀測y∈RM。最后通過求解如下l1最小范數(shù)下的最優(yōu)化問題,，從y∈RM中恢復信號x：

　　目前對式（1）的求解算法主要有匹配跟蹤法[5]等,。另外，為了保證算法的收斂性,，壓縮感知方法中選取的觀測矩陣必須滿足約束等距性[6]（Restricted Isometry Property,，RIP）。參考文獻[7]例舉了部分滿足RIP條件的觀測矩陣。

　　概括起來,，CS理論主要涉及三個方面的內(nèi)容：（1）對信號x∈RN,，如何找到某個正交基或緊框架，使其在上的表示是稀疏的,，即信號的稀疏表示,；（2）如何構造一個與變換基不相關的M×N維的觀測矩陣[8-9]，保證稀疏向量從N維降低到M維時重要的信息不遭破壞,，即信號低速采樣問題,；（3）如何設計快速重建算法從線性觀測中恢復信號，即信號重構問題,。CS理論框架如圖1所示,。

2 壓縮感知域內(nèi)圖像融合

　　基于壓縮感知的圖像融合算法的主要思想：首先對兩幅圖像進行稀疏化處理，對得到的數(shù)據(jù)利用觀測矩陣壓縮觀測,，然后確定融合規(guī)則進行數(shù)據(jù)融合,，最后通過求解最優(yōu)化問題，重構得到融合圖像,。

　　2.1 壓縮感知域圖像融合算法實現(xiàn)

　　本文融合規(guī)則采取一種改進的基于權重的方法,，先對待融合數(shù)據(jù)進行簡單的歸一化操作，再根據(jù)圖像壓縮感知域數(shù)據(jù)能量大小的不同確定待融合數(shù)據(jù)應占權重,，最后選取各數(shù)據(jù)權重值之和作為融合數(shù)據(jù),。基于壓縮感知方法的圖像融合框圖如圖2,。

　　基于壓縮感知圖像融合算法步驟如下：

　?。?）取源圖像A和B各像素點灰度值與該圖像最大灰度值之比作為輸入數(shù)據(jù)分別進行DCT變換，得到稀疏數(shù)據(jù)DCT_A和DCT_B,；

　　（2）對稀疏數(shù)據(jù)利用觀測矩陣?椎進行觀測,，觀測矩陣性能越好,，則重建信號與原始信號的誤差值越小，獲得的重建信號質(zhì)量越高,。本文觀測矩陣采取DCT域觀測矩陣設計,，獲得CS域數(shù)據(jù)值T1和T2：

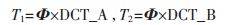
　　（3）對CS域數(shù)據(jù)采用改進的基于權重的方法進行融合,，得到融合后的數(shù)據(jù)S,。

　　改進的基于權重的融合方法框圖如圖3。

　　該方法首先計算出輸入圖像灰度均值Aij：

　　其中,，M,、N分別為源圖像的長度與寬度，Dij為源圖像灰度值。由式（2）分別計算出源圖像數(shù)據(jù)能量大小,，得到融合系數(shù)C1,、C2：

　　由此確定兩組圖像融合系數(shù)應占權重W：

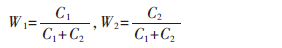
    所要求的融合后的數(shù)據(jù)即為：

　　S=W1T1（i，j）+W2T2（i,，j）（4）

　?。?）運用最小全變分法[10]對融合數(shù)據(jù)S進行重構，得到融合后圖像,。

　　2.2 DCT域觀測矩陣的設計

　　基于圖像經(jīng)離散余弦變換后的大部分系數(shù)都變?yōu)?或近似于0,，且圖像主要信息集中在左上角這一特性，設計出一種適用于DCT域測量采樣的射線采樣矩陣,，這種觀測矩陣采樣部分用數(shù)值1表示,，被拋棄的數(shù)據(jù)用0表示。具體實現(xiàn)步驟如下：

　?。?）基本參數(shù)的設定：圖像的大小N×N,，測量角度數(shù)M，像素自增步長λ,，界限距離D,，測量矩陣Matrix初始化為一個N維零矩陣；

　?。?）角度循環(huán)：測量角度從0到Pi均勻劃分為M份,，第i個測量角度記為T（i），相應的斜率為K=tanT（i）,；

　?。?）像素循環(huán)：通過內(nèi)外兩個循環(huán)實現(xiàn)圖像每一個測量角度和每一個像素點的遍歷。其中,，外循環(huán)控制矩陣行值a,，行值為0~N，每次自增λ,；內(nèi)循環(huán)控制矩陣列值b,，列值為0~N，每次自增λ,。

　?。?）測量矩陣值的確定：通過判斷圖像像素點（a，b）到各個角度確定的直線y=Kx的距離d來設定測量矩陣每一個元素的值,，其中：

　　若d>D,，則matrix（a，b）=0,，若d≤D,，則matrix（a,，b）=1。

　　這里設定輸入?yún)?shù)N=256,，M=220,，λ=0.5，D=0.5,，可以得到如圖4所示的測量矩陣,。矩陣代表數(shù)據(jù)1的白色部分為采樣數(shù)據(jù)，所占面積表明采樣數(shù)據(jù)約占整體數(shù)據(jù)的三分之一,，且主要集中在圖像左上角部分,，很好地滿足了DCT域有效信息主要集中在圖像左上角部分的特性，因此該采樣矩陣理論上能取得較好的采樣效果,。

3 實驗和結果分析

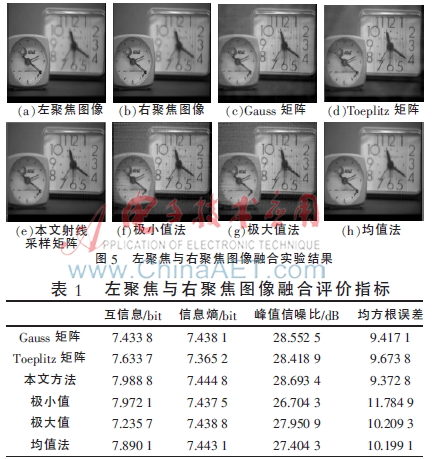
　　圖5（a）和圖5（b）為左聚焦與右聚焦clock圖像,，圖5（c）、（d）,、（e）分別為Gauss,、Toeplitz和本文射線采樣矩陣下的融合圖像，圖5（f）,、（g）,、（h）為射線采樣矩陣下融合規(guī)則分別選取極小值、極大值和均值法的融合圖像,。表1是該組實驗融合評價指標的對比,。

　　主觀視覺觀察，本文方法獲得的圖5（e）在紋理和清晰度上都優(yōu)于前兩種方法獲得的圖5（c）和圖5（d）,?？陀^地從評價指標來看，表1的前三行數(shù)據(jù)顯示,，射線采樣矩陣下獲得的互信息最大,，表示融合圖像從源圖像中獲取了更為豐富的圖像特征信息。在反應圖像本身信息量的指標信息熵和峰值信噪比上,，本文方法也取得了更好的效果,。而在反應融合誤差大小的指標上，本文方法獲得的均方根誤差值最小,。比較射線采樣矩陣下不同融合規(guī)則的實驗結果，本文改進的基于權重的方法獲得的圖5（e）圖像質(zhì)量要高于另外三種方法獲得的圖5（f）,、（g）,、（h）。對比表1后四行數(shù)據(jù),，本文方法互信息,、信息熵和峰值信噪比都相對較高，而均方根誤差相對較低?；诖?，本文的融合方法相對于極大、極小和均值法所取得的融合效果有顯著提高,，且本文提出的觀測矩陣的設計方法是切實有效的,。

　　為了驗證算法的有效性，再選取一組紅外與可見光圖像進行融合實驗,。這一組實驗中,，圖6（a）和圖6（b）為紅外與可見光filed圖像，圖6（c）,、（d）,、（e）分別為Gauss、Toeplitz和射線采樣矩陣下的融合圖像,，圖6（f）,、（g）、（h）為射線采樣矩陣下融合規(guī)則分別選取極小值,、極大值和均值法的融合圖像,。表2為該組實驗融合評價指標的對比。

　　主觀視覺上可以看出,，本文方法相比其他幾種方法能獲得更清晰的融合圖像,，客觀上評價指標也優(yōu)于其他幾種方法。因此該方法能保留原圖像更為豐富的圖像信息,。兩組實驗結果充分驗證了本文算法的可行性和有效性,。上述實驗結果也體現(xiàn)了壓縮感知方法應用到圖像融合領域的優(yōu)越性，它在大大減少數(shù)據(jù)采樣量的基礎上仍能獲得相對有效的融合效果,。

4 結束語

　　壓縮感知理論對圖像處理領域具有重要意義,。本文把壓縮感知的方法運用到圖像融合中，并著重探討了觀測矩陣對融合效果的影響,。根據(jù)DCT域的稀疏特性設計出一種射線采樣矩陣,，實現(xiàn)了較少采樣數(shù)據(jù)基礎上良好的融合效果。實驗結果表明該矩陣的設計使得融合效果在各個方面都有相應的改善,。本文也通過實驗得出,，改進的基于權重的融合方法能提高融合質(zhì)量。

　　參考文獻

　　[1] 焦李成,，楊淑媛,，劉芳，等.壓縮傳感回顧與展望[J].電子學報,，2011,，39（7）：1651-1662.

　　[2] DONOHO D. Compressed sensing[J]. IEEE Trans. Information Theory,， 2006， 52（4）：1289-1306.

　　[3] CANDES E J .Compressive sampling[C]. Proceedings of the International Congress of Mathematicians,， Spain,， 2006： 1433-1452.

　　[4] 李衛(wèi)光，李躍,，張修社.圖像信息融合與識別[M].北京：電子工業(yè)出版社,，2008.

　　[5] TROPP J， GILBERT A. Signal recovery from random measurements via orthogonal matching pursuit[J]. Trans on Information Throry,， 2007,，53（12）：4655-4666.

　　[6] LIN T， YU P. Adaptive two-pass median filter based on support vector Machinesfor image restoration[J]. Neural Computation,， 2004,，16（2）：5406-5425.

　　[7] TRZASKO J， MANDUCA A. Highly undersampled magnetic resonance image  reconstructionvia homotopic ell-0 minimization[J]. IEEE Transactions on Medical Imaging,， 2009,，28（1）：106-121.

　　[8] 潘匯，張勁東,，張弓.壓縮感知雷達感知矩陣優(yōu)化[J].數(shù)據(jù)采集與處理,，2012，27（2）：138-143.

　　[9] 李小波.基于壓縮感知的測量矩陣研究[D].北京：北京交通大學,，2010.

　　[10] CANDES E,， ROMBERG J， TAO T. Robust uncertaintyprinciples： exact signal reconstruction from  highly incomplete frequency information[J]. IEEE Transactions on Information Theory,， 2006,，52（2）：489-509.