摘 要： 針對(duì)梯形箱子的三維裝箱問題，提出了一種基于空間分割的構(gòu)造性啟發(fā)式算法,，根據(jù)梯形箱子三維裝箱問題的特點(diǎn),，設(shè)計(jì)了相應(yīng)的空間分割策略、空間合并策略與空間重組策略,，在此基礎(chǔ)上加入遺傳算法,，提高算法局部與全局搜索能力。實(shí)驗(yàn)結(jié)果表明，該算法能有效處理梯形箱子三維裝箱問題,。
關(guān)鍵詞： 三維裝箱問題,；啟發(fā)式算法；遺傳算法
0 引言
裝箱問題（Bin Packing Problem）在現(xiàn)實(shí)生活中具有廣泛的應(yīng)用,。計(jì)算機(jī)領(lǐng)域中有內(nèi)存分配,、信息存儲(chǔ)等一維裝箱問題；二維裝箱問題應(yīng)用于服裝裁剪,、新聞排版,、矩形裝箱[1]等；在貨運(yùn)碼頭,、物流,、倉(cāng)儲(chǔ)等領(lǐng)域則涉及三維裝箱問題。
裝箱問題是NP難問題,，需要考慮維數(shù),、形狀、約束,、目標(biāo)等不同因素,，因此理論研究與實(shí)際工程應(yīng)用中一般采用近似算法。近年來,，國(guó)內(nèi)外學(xué)者對(duì)三維裝箱問題進(jìn)行了廣泛而深入的研究,。三維裝箱問題存在禁忌搜索算法[2]、遺傳算法[3-4],、模擬退火算法[5]等研究和應(yīng)用,。參考文獻(xiàn)[6]采用動(dòng)態(tài)空間分解方法進(jìn)行啟發(fā)式裝載，其對(duì)剩余空間進(jìn)行重組優(yōu)化存在不足,；參考文獻(xiàn)[5]提出了混合模擬退火算法,，從一個(gè)初始貨物裝載序列采用模擬退火搜索一個(gè)好的貨物裝載序列，作為問題的近似解,；參考文獻(xiàn)[7]通過組織裝填樹把大空間分成小空間進(jìn)行裝填,，最后再對(duì)剩余空間進(jìn)行處理，其通過搜索局部最優(yōu)解進(jìn)行裝填,，全局搜索能力需要提高,；另外還有一些基于“塊”的啟發(fā)式算法[8-10]與運(yùn)用“墻”的建立與穴度方法相組合的啟發(fā)式算法[11]，這些啟發(fā)式算法是面向長(zhǎng)方體箱子三維裝箱問題算法研究應(yīng)用,，而沒有涉及到梯形箱子的三維裝箱問題,。
在實(shí)際工程應(yīng)用中存在非長(zhǎng)方體箱子三維裝箱問題，例如,，箱子幾何形狀為上下底面為直角梯形的直四棱柱等特殊類型的箱子,。這需要根據(jù)具體裝箱問題的特點(diǎn)與實(shí)際工程應(yīng)用要求,，研究相應(yīng)的裝箱算法來完成貨物裝箱。
本文研究的梯形箱子三維裝箱問題的具體描述為：給定無限數(shù)量相同規(guī)格的梯形箱子,，給定有限數(shù)量的待裝長(zhǎng)方體貨物,，在滿足裝載約束的條件下把這些長(zhǎng)方體貨物全部裝入梯形箱子中，目標(biāo)是梯形箱子使用數(shù)目最少,，使空間利用率最高,。
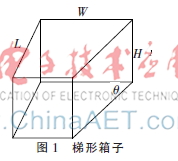
定義1（梯形箱子） 梯形箱子的幾何形狀是上下底面為直角梯形的直四棱柱，在圖1中,，其幾何形狀可以通過底面直角梯形的高度L,、底面直角梯形的下底邊W、底面直角梯形的銳角θ以及直四棱柱高度H來描述,。
裝載約束條件如下：
?。?）每個(gè)裝載的貨物不能與其他裝載貨物或者梯形箱子互相重疊,；
?。?）每個(gè)裝入梯形箱子的貨物的每一個(gè)面必須與梯形箱子的某一個(gè)面平行；
?。?）每個(gè)裝入梯形箱子的貨物必須滿足方向約束,。
1 基于空間分割的構(gòu)造性啟發(fā)式算法
針對(duì)梯形箱子三維裝箱問題，本文提出了一種基于空間分割的構(gòu)造性啟發(fā)式算法,。該算法思想借鑒了Bortfeld和Gehring[2]中提到的基礎(chǔ)啟發(fā)式算法,。
1.1 空間分割
在裝箱問題中，所有裝入的貨物都是與坐標(biāo)軸平行的長(zhǎng)方體,，對(duì)它們的裝載位置描述是通過參考點(diǎn)與各個(gè)維度上的邊長(zhǎng)來確定的,。圖2中空間直角坐標(biāo)系的X軸、Y軸,、Z軸分別與梯形箱子長(zhǎng)度L,、寬度W、高度H方向平行,，梯形箱子左后下角為原點(diǎn)O,。
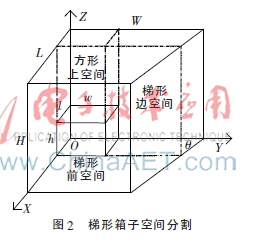
定義2（方形空間）方形空間i由其幾何形狀長(zhǎng)度Li、寬度Wi和高度Hi,，以及空間坐標(biāo)參考點(diǎn)（xi,，yi，zi）構(gòu)成,，數(shù)學(xué)表達(dá)方式：
cspacei={（Li,，Wi，Hi）,，（xi,，yi，zi）}（1）
定義3（梯形空間）梯形空間i由其幾何形狀長(zhǎng)度Li、寬度Wi,、高度Hi和底面直角梯形的銳角θ,，以及空間坐標(biāo)參考點(diǎn)（xi，yi,，zi）構(gòu)成,，數(shù)學(xué)表達(dá)方式：
tspacei={（Li，Wi,，Hi,，θi），（xi,，yi,，zi）}（2）
把梯形箱子作為一個(gè)梯形空間tspacei，當(dāng)某個(gè)長(zhǎng)寬高為（lj,，wj,，hj）的貨物j滿足梯形空間約束時(shí)，該貨物裝入梯形空間的空間坐標(biāo)參考點(diǎn)（xi,，yi,，zi）即原點(diǎn)O，剩余空間被分割成3個(gè)子空間：
方形上空間
cspacea={（lj,，wj,，Hi-hj），（xi,，yi,，zi+hj）}（3）
梯形邊空間
tspaceb={（lj，Wi-wj,，Hi,，θi），（xi,，yi+wj,，zi）}（4）
梯形前空間
tspacec={（Li-lj，Wi-lj/tanθi,，Hi,，θi），（xi+lj,，yi,，zi）}（5）
梯形空間約束：
當(dāng)貨物j裝入梯形空間tspacei時(shí)需滿足：
lj≤Li且hj≤Hi且（wj+lj/tanθi）≤Wi（6）
由所有子空間構(gòu)成一個(gè)空間集合S，從空間集合中選擇一個(gè)子空間,，若是梯形空間則分割方法如上,，若是方形子空間則采用方法如下：
選擇一個(gè)方形空間cspacei,，當(dāng)某個(gè)長(zhǎng)、寬,、高為（lj,，wj，hj）的貨物j滿足方形空間約束時(shí),，該貨物裝入方形空間的空間坐標(biāo)參考點(diǎn)（xi,，yi，zi）,，剩余空間被分割成3個(gè)子空間：
方形上空間
cspaced={（lj,，wj，Hi-hj）,，（xi,，yi，zi+hj）}（7）
方形邊空間
cspacee={（lj,，Wi-wj,，Hi），（xi,，yi+wj,，zi）}（8）
方形前空間
cspacef={（Li-lj,，Wi,，Hi），（xi+lj,，yi,，zi）}（9）
方形空間約束：
當(dāng)貨物j裝入方形空間cspacei時(shí)需滿足：
lj≤Li且hj≤Hi且wj≤Wi（10）
1.2 啟發(fā)式算法
基于空間分割的啟發(fā)式算法基本步驟表述如下：
（1）算法開始,，初始化待裝貨物序列C與梯形箱子信息,。
（2）判斷待裝貨物是否裝載完成,，裝載完成跳轉(zhuǎn)（7）,；反之，未完成裝載則跳轉(zhuǎn)到（3）,。
?。?）選擇一個(gè)待裝貨物并開啟一個(gè)新的梯形箱子，待裝貨物裝入梯形箱子后剩余空間被分割成3個(gè)子空間,，分別為方形上空間,、梯形邊空間與梯形前空間，這3個(gè)子空間組成新的空間序列S,，把裝入的貨物從待裝貨物序列C中移除,，完成待裝貨物序列C更新,。
（4）判斷待裝貨物序列C中是否存在一個(gè)貨物滿足裝載約束并能裝入空間序列S中某個(gè)空間,，存在該貨物則跳轉(zhuǎn)（5）,；反之，則跳轉(zhuǎn)到（6）,。
?。?）若該空間為梯形子空間，裝入選擇的貨物后,，剩余空間被分割為方形上空間,、梯形邊空間與梯形前空間這3個(gè)子空間；若該空間為方形子空間,，則裝入選擇的貨物后,，剩余空間被分割為方形上空間、方形邊空間與方形前空間這3個(gè)子空間,；該空間裝入貨物后從空間序列S中移除,，新生成的3個(gè)子空間添加到空間序列S中，同時(shí)通過空間合并策略更新空間序列S,，裝入的貨物從待裝貨物序列C中移除,，完成待裝貨物序列C更新。
?。?）判斷是否進(jìn)行過重組策略操作,，沒有則對(duì)空間序列S進(jìn)行重組策略操作，跳轉(zhuǎn)（4）,；若進(jìn)行過重組策略操作則跳轉(zhuǎn)到（2）,。
（7）輸出梯形箱子三維裝箱方案,，算法結(jié)束,。
定義4（空間合并策略）若2個(gè)方形子空間cspace1={（L1，W1,，H1）,，（x1，y1,，z1）},、cspace2={（L2，W2,，H2）,，（x2，y2,，z2）}能夠滿足以下條件中的一個(gè)：
條件1：（L1+x1==x2||L2+x2==x1）&&（y1==y2）&&（W1==W2）&&（z1==z2）&&（H1==H2）（11）
條件2：（W1+y1==y2||W2+y2==y1）&&（x1==x2）&&（L1==L2）&&（z1==z2）&&（H1==H2）（12）
則2個(gè)方形子空間合并為新的方形子空間cspace3,。
若滿足條件1,，則：
if x1<x2 cspace3={（L1+L2，W1,，H1）,，（x1，y1,，z1）},；（13）
if x2<x1 cspace3={（L1+L2，W2,，H2）,，（x2，y2,，z2）},；（14）
若滿足條件2，則：
if y1<y2 cspace3={（L1,，W1+W2,，H1），（x1,，y1,，z1）}；（15）
if y2<y1 cspace3={（L2,，W1+W2,，H2），（x2,，y2,，z2）},；（16）
空間合并策略是把2個(gè)能合并的子空間合并成一個(gè)更大的子空間,，提高箱子的空間利用率。
圖3（a）為滿足條件1的空間合并示意圖,，圖3（b）為滿足條件2的空間合并示意圖,。
定義5（空間重組策略）若2個(gè)方形子空間cspace4={（L4，W4,，H4）,，（x4，y4,，z4）},、cspace5={（L5，W5,，H5）,，（x5,，y5，z5）}能夠滿足以下條件中的一個(gè)：
條件3：（L4+x4==x5||L5+x5==x4）&&（y4==y5）&&（W4==W5）&&（z4+H4==z5+H5）（17）
條件4：（W4+y4==y5||W5+y5==y4）&&（x4==x5）&&（L4==L5）&&（z4+H4==z5+H5）（18）
則2個(gè)方形子空間重組為新的方形子空間cspace6,。
令H6=min（H4,，H5），z6=max（z4,，z5）,；（19）
若滿足條件3，則：
if x4<x5 cspace6={（L4+L5,，W4,，H6），（x4,，y4,，z6）}；（20）
if x5<x4 cspace6={（L4+L5,，W5,，H6），（x5,，y5,，z6）}；（21）
若滿足條件4,，則：
if y4<y5 cspace6={（L4,，W4+W5，H6）,，（x4,，y4，z6）},；（22）
if y5<y4 cspace6={（L5,，W4+W5，H6）,，（x5,，y5，z6）},；（23）
空間重組策略是充分利用剩余的子空間,，有利于提高箱子的空間利用率。圖4為空間重組示意圖,。
2 面向梯形箱子三維裝箱的混合遺傳算法
針對(duì)梯形箱子三維裝箱問題這一NP難問題,，結(jié)合啟發(fā)式算法局部搜索能力與遺傳算法全局搜索能力，混合遺傳算法不僅局部搜索能力得到加強(qiáng),，而且兼具全局搜索能力,。
2.1 編碼方案
根據(jù)梯形箱子三維裝箱問題的具體情況,，采用順序編碼，每個(gè)個(gè)體由待裝貨物編號(hào)序列PN以及其對(duì)應(yīng)的擺放方向序列PD組成,。貨物的擺放方向有6種,，對(duì)應(yīng)編號(hào)1為（l，w,，h）,、編號(hào)2為（w，l,，h）,、編號(hào)3為（w，h,，l）,、編號(hào)4為（h，w,，l）,、編號(hào)5為（l，h,，w）,、編號(hào)6為（h，l,，w）,。
2.2 適應(yīng)度函數(shù)
通過個(gè)體適應(yīng)度的大小來評(píng)價(jià)群體中個(gè)體所對(duì)應(yīng)裝載方案的優(yōu)劣。這里選擇整體梯形箱子三維裝箱空間利用率作為適應(yīng)度函數(shù)：
其中,，M表示裝載了M個(gè)貨物,，lj，wj,，hj表示第j件貨物的長(zhǎng)度,、寬度和高度；N表示使用了N個(gè)梯形箱子,，Vi表示第i個(gè)梯形箱子的體積,。
2.3 遺傳操作
采用輪盤賭選擇方法作為選擇算子，在輪盤賭選擇中,，各個(gè)個(gè)體的選擇概率與其適應(yīng)度值成正比例。
采用部分匹配交叉（Partally Matched Crossover,，PMX）算子,，在PMX操作中，先依據(jù)均勻隨機(jī)分布產(chǎn)生兩個(gè)位串交叉點(diǎn),，這兩點(diǎn)之間的區(qū)域?yàn)橐黄ヅ鋮^(qū)域,，并使用位置交換操作交換兩個(gè)父串的匹配區(qū)域,。
對(duì)進(jìn)行變異操作的個(gè)體，隨機(jī)產(chǎn)生2個(gè)位置i,、j,，交換處在位置i與位置j上的貨物編號(hào)信息n及對(duì)應(yīng)的貨物方向信息；存在一定變異概率使得貨物擺放方向變異,。變異算子的作用是維持群體的多樣性,，避免算法早熟收斂。
圖5為面向梯形箱子三維裝箱的混合遺傳算法流程圖,。
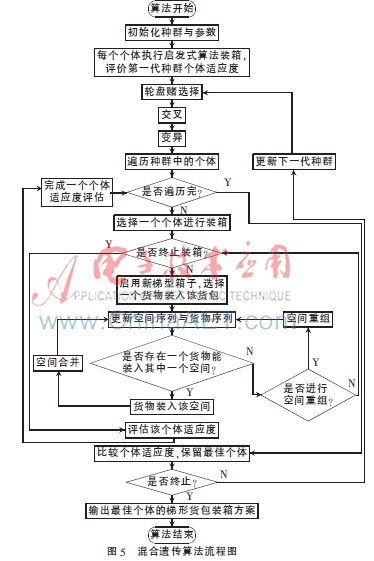
3 實(shí)驗(yàn)結(jié)果
表1中測(cè)試用例1~4,，使用梯形箱子參數(shù)為L(zhǎng)=400、W=800,、H=400,、tanθ=1；測(cè)試用例5~8,，使用梯形箱子參數(shù)為L(zhǎng)=400,、W=600、H=400,、tanθ=2,；測(cè)試用例9~12，使用梯形箱子參數(shù)為L(zhǎng)=400,、W=900,、H=400、tanθ=0.8,；混合遺傳算法參數(shù)設(shè)置：種群大小20,、進(jìn)化代數(shù)100、交叉概率0.5,、變異概率0.05,；每個(gè)測(cè)試用例進(jìn)行100次實(shí)驗(yàn)。本文混合遺傳算法與混合模擬退火算法[5]進(jìn)行比較,。
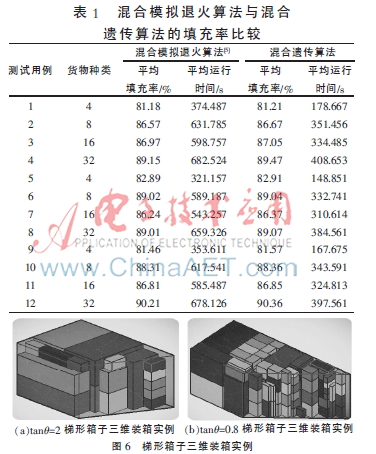
表1的實(shí)驗(yàn)結(jié)果顯示,，在面向梯形箱子三維裝箱問題上，通過與混合模擬退火算法比較,，混合遺傳算法的解不僅平均空間填充率較高,，而且平均運(yùn)行時(shí)間較短?；旌线z傳算法能有效處理梯形箱子三維裝箱問題,。
圖6中，（a）是測(cè)試用例5的一個(gè)空間填充率為87.24%的梯形箱子三維裝箱布局方案實(shí)例，（b）是測(cè)試用例12的一個(gè)空間填充率為92.11%的梯形箱子三維裝箱布局方案實(shí)例,。
4 結(jié)論
借鑒Bortfeld和Gehring[2]的長(zhǎng)方體空間基礎(chǔ)啟發(fā)式算法思想,，根據(jù)梯形箱子的空間約束條件，研究設(shè)計(jì)了面向梯形空間的構(gòu)造性啟發(fā)式算法,。采用空間分割策略,、空間合并策略與空間重組策略提高局部搜索能力。其與遺傳算法全局搜索能力相結(jié)合,，設(shè)計(jì)了面向梯形箱子三維裝箱問題的混合遺傳算法,。理論分析與實(shí)驗(yàn)結(jié)果顯示，針對(duì)梯形箱子三維裝箱問題,，混合遺傳算法具有良好的優(yōu)化效果,。希望本文的研究對(duì)三角形箱子、楔形箱子等特定類型箱子三維裝箱問題的研究提供一些幫助和借鑒,。
參考文獻(xiàn)
[1] 陳勝達(dá),，張德富，劉艷娟.求解矩形裝箱問題的一種近似算法[J].計(jì)算機(jī)工程,，2007,，33（9）：189-193.
[2] BORTFELDT A， GEHRING H,， MACK D. A parallel tabu search algorithm for solving the container loading problem[J]. Parallel Computing,，2003，29（5）：641-662.
[3] BORTFELDT A,， GEHRING H. A hybrid genetic algorithm for the container loading problem[J]. European Journal of Operational Research,，2001，131（1）：143-161.
[4] GEHRING H,， BORTFELDT A. A parallel genetic algorithm for solving the container loading problem[J]. International Transactions in Operational Research,，2002，9（4）：497-511.
[5] 張德富,，彭煜,，朱文興，等.求解三維裝箱問題的混合模擬退火算法[J].計(jì)算機(jī)學(xué)報(bào),，2009,，32（11）：2148-2156.
[6] WANG Z， LI K W,， LEVY J K. A heuristic for the container loading problem： a tertiary-tree-based dynamic space decomposition approach[J]. European Journal of Operational Research,，2008，191（1）：86-99.
[7] LIM A,， RODRIGUES B,， YANG Y. 3-D container packing heuristics[J]． Applied Intelligence,，2005,，22（2）：125-134.
[8] 張德富,，彭煜，張麗麗.求解三維裝箱問題的多層啟發(fā)式搜索算法[J].計(jì)算機(jī)學(xué)報(bào),，2012,，35（12）：2554-2561.
[9] MIYAZAWA F K，.WAKABAYASHI Y. Three-dimensional packings with rotations[J]. Computers & Operations Research,，2009,，36（10）：2801-2815.
[10] ELEY M. Solving container loading problems by block arrangement[J]. European Journal of Operational Research，2002,，141（2）：393-409.
[11] Wu Xiuli,， Du Yanhua， Li Sujian. A new approach for the three-dimensional single container loading problem[C]. Intelligent Human-Machine Systems and Cybernetics （IHMSC）,， 2013 5th International Conference on,， 2013：155-158.
[12] 陳國(guó)良，王煦法,，莊鎮(zhèn)泉,，等.遺傳算法及其應(yīng)用[M].北京：人民郵電出版社，1996.