摘 要: 稀疏優(yōu)化后的同心圓陣的旁瓣電平雖然相比于滿陣有所降低,但還是很高。為了獲得具有更低旁瓣電平的同心圓陣,本文采用錐型波束形成技術(shù),對(duì)利用模擬退火粒子群算法得到的稀疏同心圓陣加窗,優(yōu)化陣列饋電電流的激勵(lì)振幅。利用改進(jìn)的三角窗、漢寧窗和布萊克曼窗三種窗函數(shù)對(duì)稀疏同心圓陣進(jìn)行優(yōu)化。仿真結(jié)果表明,加窗后,稀疏同心圓陣的旁瓣電平都有明顯降低,采用布萊克曼窗得到的陣列的最大旁瓣電平最小,漢寧窗的次之,三角窗的最大。
關(guān)鍵詞: 稀疏同心圓陣;窗函數(shù);旁瓣電平
0 引言
同心圓陣天線[1-2]具有結(jié)構(gòu)簡(jiǎn)單、掃描范圍寬、波束方位控制靈活等特點(diǎn),被廣泛應(yīng)用于雷達(dá)、聲吶、移動(dòng)通信和電子系統(tǒng)中。但同時(shí)存在陣列陣元數(shù)目較多、系統(tǒng)成本大、旁瓣電平高等缺點(diǎn)。稀疏陣列天線[3-6]能有效解決以上問(wèn)題。然而稀疏后的陣列天線的旁瓣電平往往較高,為了進(jìn)一步降低同心圓陣的旁瓣電平,采用錐型波束形成技術(shù),對(duì)陣列饋電電流的激勵(lì)振幅進(jìn)行優(yōu)化,使陣列中心圓環(huán)的陣元激勵(lì)振幅最大,最外環(huán)的陣元激勵(lì)振幅最小。
一種錐型波束形成的方法是在濾波器中進(jìn)行波束形成,通過(guò)窗函數(shù)改善阻帶特征[7]。但要對(duì)信號(hào)濾波中的窗函數(shù)進(jìn)行改進(jìn),使之適用于具有同心圓結(jié)構(gòu)的陣列天線。本文分別將改進(jìn)的三角窗、漢寧窗和布萊克曼窗應(yīng)用到稀疏同心圓陣中,比較其陣列方向圖,分析其性能。
1 同心圓陣
同心圓陣是由多個(gè)具有共同圓心的均勻圓陣組成的平面陣,如圖1。
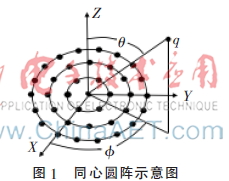
對(duì)于陣列天線,如果陣元間距超過(guò)信號(hào)半波長(zhǎng),陣列方向圖會(huì)出現(xiàn)高的柵瓣。然而如果陣元間距小于半波長(zhǎng),陣列方向圖會(huì)有較寬的主瓣寬度,而且陣元間的互耦效應(yīng)會(huì)增大。因此,設(shè)計(jì)同心圓陣列天線時(shí),每個(gè)圓環(huán)上的陣元間距設(shè)置為半波長(zhǎng)。
設(shè)均勻同心圓陣由M個(gè)圓環(huán)構(gòu)成,每個(gè)圓環(huán)之間間隔dc=λ/2,每個(gè)圓環(huán)的半徑rm=mλ/2。位于同一圓環(huán)上的陣元等間隔均勻分布,每個(gè)圓環(huán)上的陣元間距dm≈λ/2,則第m個(gè)圓環(huán)上的陣元個(gè)數(shù):
Nm=2πrm/dm=2πm(1)
陣元的個(gè)數(shù)應(yīng)該是整數(shù),由式(1)得到的結(jié)果要向下取整。
把圓心位置的陣元作為陣列的參考陣元,陣元為理想的全向性天線單元,各陣元等幅同向激勵(lì),陣列主波束指向陣列中心法線方向,同心圓陣方向圖函數(shù)為:
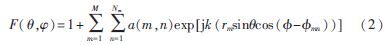
其中,![WB]05SG11}OXJC`__HAL4CA.jpg WB]05SG11}OXJC`__HAL4CA.jpg](http://files.chinaaet.com/images/2016/02/23/6359184739312100009957115.jpg) 為第m個(gè)圓環(huán)上第n個(gè)陣元對(duì)應(yīng)的方位角,
為第m個(gè)圓環(huán)上第n個(gè)陣元對(duì)應(yīng)的方位角,![WB]05SG11}OXJC`__HAL4CA.jpg WB]05SG11}OXJC`__HAL4CA.jpg](http://files.chinaaet.com/images/2016/02/23/6359184739933000002904269.jpg) =2π(n-1)/Nm;k=2π/λ,λ為信號(hào)波長(zhǎng);a(m,n)為第m個(gè)圓環(huán)上第n個(gè)陣元對(duì)應(yīng)的陣元激勵(lì)。
=2π(n-1)/Nm;k=2π/λ,λ為信號(hào)波長(zhǎng);a(m,n)為第m個(gè)圓環(huán)上第n個(gè)陣元對(duì)應(yīng)的陣元激勵(lì)。
2 稀疏同心圓陣
為保證陣列稀疏優(yōu)化時(shí)仍滿足陣列孔徑約束條件,同心圓陣圓心位置的陣元需保留,不能被稀疏掉。A為陣列中各個(gè)陣元位置的幅度加權(quán)系數(shù)a(m,n)構(gòu)成的矩陣,以a(m,n)表示該柵格處是否放置陣元。當(dāng)amn=1時(shí),代表該位置有陣元;當(dāng)amn=0時(shí),代表該位置無(wú)陣元。采用粒子群算法稀疏優(yōu)化同心圓陣,系數(shù)矩陣A映射為一個(gè)粒子,粒子中的一個(gè)變量對(duì)應(yīng)于一個(gè)陣元。以降低同心圓陣天線的旁瓣電平為優(yōu)化目標(biāo),利用其最大旁瓣電平構(gòu)造目標(biāo)函數(shù),即:

其中,F(xiàn)max為主瓣電平,F(xiàn)sll max為最大旁瓣電平。目標(biāo)函數(shù)值越小,則旁瓣電平越小,陣列天線性能越好。
粒子的目標(biāo)函數(shù)值決定粒子的位置是否最優(yōu)。在每次迭代中,粒子根據(jù)以往經(jīng)驗(yàn)尋找最優(yōu)粒子位置,并通過(guò)跟蹤兩個(gè)“最優(yōu)”粒子的位置來(lái)不斷更新:一個(gè)是單個(gè)粒子迄今找到的最優(yōu)解位置,即個(gè)體最優(yōu)位置;另一個(gè)是整個(gè)群體迄今找到的最優(yōu)解位置,即全局最優(yōu)位置。
利用粒子群算法對(duì)同心圓陣進(jìn)行稀疏優(yōu)化的算法流程如圖2所示,其中pbsed是個(gè)體最優(yōu),gbest是全局最優(yōu)。
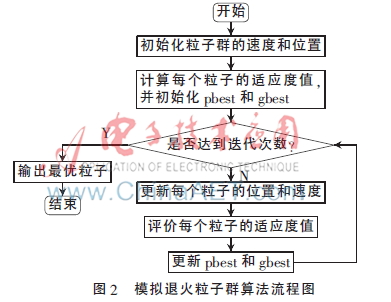
3 對(duì)稀疏同心圓陣加窗
前文對(duì)同心圓陣進(jìn)行稀疏時(shí),陣列中各單元為等幅激勵(lì)。為了獲得旁瓣電平更低的同心圓陣,對(duì)陣元激勵(lì)進(jìn)行優(yōu)化,使陣元激勵(lì)具有錐型幅度分布,對(duì)稀疏同心圓陣加窗。窗函數(shù)即為截?cái)嗪瘮?shù),采用不同的截?cái)嗪瘮?shù)對(duì)陣元激勵(lì)的振幅進(jìn)行截?cái)啵源藴p小陣列天線的旁瓣電平。
加窗時(shí),陣列的同一圓環(huán)上的振幅權(quán)重相同,最中心陣元激勵(lì)的振幅權(quán)重最大,由里到外圓環(huán)陣元激勵(lì)的振幅隨窗函數(shù)變化,最外圓環(huán)的振幅權(quán)重最小。
3.1 三角窗
對(duì)同心圓陣加三角窗,同心圓陣每個(gè)圓環(huán)的陣元激勵(lì)振幅權(quán)重隨三角函數(shù)變化,其變化公式如下:
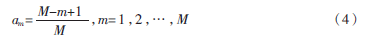
其中,m是指同心圓陣的第m個(gè)圓環(huán),M為同心圓陣的圓環(huán)個(gè)數(shù)。同心圓陣的最里圓環(huán)的陣元激勵(lì)振幅權(quán)重為am=1,最外圓環(huán)的陣元激勵(lì)振幅權(quán)重為am=1/m。
3.2 漢寧窗
漢寧窗是升余弦窗。對(duì)同心圓陣加漢寧窗,同心圓陣每個(gè)圓環(huán)的陣元激勵(lì)振幅權(quán)重隨漢寧窗函數(shù)變化,其變化公式如下:
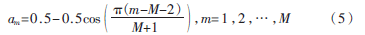
3.3 布萊克曼窗
布萊克曼窗為二階升余弦窗。對(duì)同心圓陣加布萊克曼窗,同心圓陣每個(gè)圓環(huán)的陣元激勵(lì)振幅權(quán)重隨布萊克曼窗函數(shù)變化,其變化公式如下:
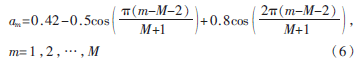
4 仿真結(jié)果
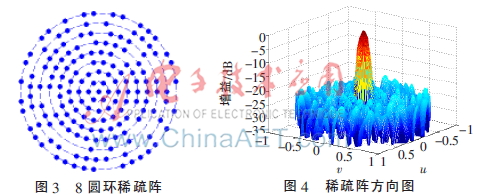
設(shè)一均勻同心9圓環(huán)陣列由223個(gè)陣元組成,陣列圓心的陣元作為第一個(gè)圓環(huán),計(jì)算可得其最大旁瓣電平為-17.37 dB。采用模擬退火粒子群算法對(duì)同心圓陣進(jìn)行稀疏優(yōu)化,得到的稀疏陣單元數(shù)為163,最大旁瓣電平為-21.72 dB,當(dāng)方位角為0時(shí),其第一零點(diǎn)波束寬度為17.91°。圖3為稀疏后同心圓陣陣元分布,以實(shí)心圓點(diǎn)代表同心圓陣陣元。稀疏優(yōu)化后的同心圓陣的方向圖如圖4所示。
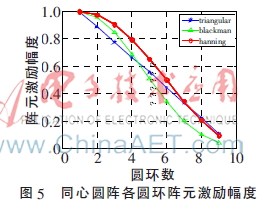
對(duì)稀疏后的同心圓陣分別加三角窗、漢寧窗和布萊克曼窗。同心圓陣圓心陣元的激勵(lì)幅度為1,圓心外8個(gè)圓環(huán)陣元激勵(lì)幅度由里到外隨窗函數(shù)依次減小,得到的陣元激勵(lì)幅度變化趨勢(shì)如圖5所示。
對(duì)稀疏同心圓陣分別加三角窗、漢寧窗和布萊克曼窗后,得到的稀疏陣列的最大旁瓣電平分別為-24.23 dB、-24.36 dB和-25.16 dB,其二維方向圖分別如圖6~8所示,三條曲線分別是方位角為0、π/4和π/2時(shí)的方向圖。當(dāng)方位角為0時(shí),得到陣列的第一零點(diǎn)波束寬度分別為31.75°、32.24°和37.61°。
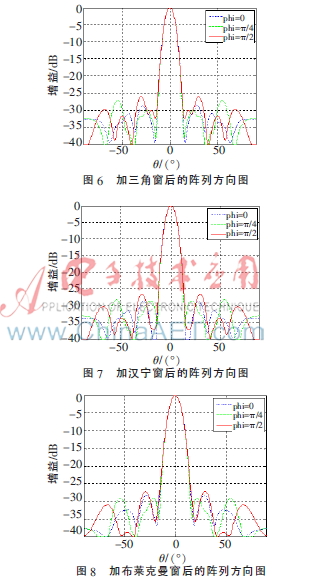
由圖6~8可以得出,加窗后稀疏陣列的最大旁瓣電平較加窗前時(shí)都有所降低,說(shuō)明對(duì)稀疏同心圓陣加窗可以降低陣列的旁瓣電平。加不同的窗,旁瓣電平降低的程度有所不同。加布萊克曼窗得到的陣列的最大旁瓣電平最小,加漢寧窗的次之,加三角窗的最大,比未加窗的稀疏陣列的最大旁瓣電平分別降低了3.44 dB、2.64 dB和2.51 dB。但陣列旁瓣電平降低的同時(shí),其第一零點(diǎn)波束寬度變寬了,加三角窗、漢寧窗和布萊克曼窗得到的稀疏陣比未加窗的稀疏陣的第一零點(diǎn)波束寬度分別展寬了13.84°、14.33°和19.70°。
5 結(jié)論
本文利用窗函數(shù)對(duì)稀疏同心圓陣的陣元激勵(lì)振幅進(jìn)行優(yōu)化,并分析了加窗后陣列的最大旁瓣電平和第一零點(diǎn)波束寬度的變化情況。通過(guò)對(duì)三種窗函數(shù)下的陣列旁瓣電平進(jìn)行比較,得出布萊克曼窗的優(yōu)化效果最好,漢寧窗次之,三角窗最差。從第一零點(diǎn)波束寬度的變化情況來(lái)看,隨著旁瓣電平的降低,主瓣寬度變寬了。利用加窗的方法降低陣列旁瓣電平是以增大第一零點(diǎn)波束寬度為代價(jià)的。
參考文獻(xiàn)
[1] CNANG B K, MA X Y, SEQUEIRA H B. Minimax-maxmini algorithm: a new approach to optimization of the thinned antenna array[C]. Antennas and Propagation Society Internatiol Symposium, Seattle, WA: IEEE Press,1994:514-517.
[2] 薛正輝,李偉明,任伍.陣列天線分析與綜合[M].北京:北京航空航天大學(xué)出版社,2011.
[3] HAUPT R L. Optimized element spacing for low sidelobe concentric ring arrays[J]. IEEE Transactions on Antennas and Propagation, 2008,56(1):266-268.
[4] HAUPT R L. Thinned arrays using genetic algorithms[J]. IEEE Transactions on Antennas and Propagation, 1994, 42(7):993-999.
[5] MANDAL D, SADHU D, GHOSHAL S P. Thinned concentric circular array antennas synthesis using improved particle swarm optimization[J]. Aceee International Journal on Communication, 2011,2(2):21-25.
[6] SINGH U, SINGH D, KAUR C. Thinning of planar circular array antennas using Firfly algorithm[C]. Engineering and Computational Sciences(RAECS), 2014 Recent Advances in. IEEE, 2014:1-5.
[7] DESSOUKY M I, SHARSHAR H A, ALBAGORY Y A. Optimum normalized-gaussian tapering window for side lobe reduction in uniform concentric circular arrays[J]. Progress in Electromagnetics Research, 2007,69(1):35-46.

