摘  要： 旅游客流量受多種因素影響,，傳統(tǒng)的時(shí)間序列預(yù)測(cè)模型無法描述預(yù)測(cè)對(duì)象的規(guī)律,，人工智能方法如BP神經(jīng)網(wǎng)絡(luò)，其結(jié)構(gòu)的選擇過多依賴經(jīng)驗(yàn),，基于此提出了利用改進(jìn)的粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò),，通過慣性因子的非線性遞減來改善粒子群的尋優(yōu)性能。將該預(yù)測(cè)模型應(yīng)用于自貢燈會(huì)的客流量進(jìn)行實(shí)際預(yù)測(cè)分析,，通過對(duì)150組訓(xùn)練樣本和50組測(cè)試樣本的實(shí)驗(yàn)仿真，可知改進(jìn)后的方法提高了預(yù)測(cè)結(jié)果的準(zhǔn)確度,，并且涉及參數(shù)少,、簡(jiǎn)單有效。

　　關(guān)鍵詞： 旅游客流量預(yù)測(cè),；BP神經(jīng)網(wǎng)絡(luò),；粒子群算法；非線性遞減

0 引言

　　隨著中國旅游日的設(shè)立和國民旅游意識(shí)的增強(qiáng)，節(jié)假日旅游成了眾多人的選擇,，但旅游目的地的接待能力有限,，游客太多則旅游設(shè)施供不應(yīng)求，服務(wù)質(zhì)量下降,，甚至出現(xiàn)游客擁堵,、踩踏等安全事故。旅游景點(diǎn)游客量預(yù)測(cè),，一直是旅游研究中的熱點(diǎn),，也是旅游學(xué)界面對(duì)的難點(diǎn)問題之一[1]。

　　傳統(tǒng)的旅游需求預(yù)測(cè),，主要是定量與定性方面的研究,，比如計(jì)量經(jīng)濟(jì)模型[2]、時(shí)間序列分析模型[3-4],、灰色預(yù)測(cè)模型[5]等方法,。然而這些方法有一定的缺陷，或者是只分析單個(gè)影響因素,，如客流量歷史數(shù)據(jù),，認(rèn)為未來是過去和現(xiàn)在的延續(xù)，或者是經(jīng)驗(yàn)對(duì)預(yù)測(cè)方法的過度干擾,，缺少對(duì)歷史數(shù)據(jù)的學(xué)習(xí)過程,。這些都會(huì)致使預(yù)測(cè)結(jié)果的不準(zhǔn)確。另外,，旅游景區(qū)每日客流量容易受到多個(gè)外部因素的影響,，如天氣、某些節(jié)假日等,，具有較強(qiáng)的波動(dòng)性和非線性,，使用計(jì)量統(tǒng)計(jì)思想建立的模型難以逼近其內(nèi)在變化機(jī)制。

　　由于具有良好的自適應(yīng)性和強(qiáng)大的非線性映射能力,，BP神經(jīng)網(wǎng)絡(luò)得到了廣泛的應(yīng)用,，但其也存在著一些不足：一是網(wǎng)絡(luò)模型訓(xùn)練前BP網(wǎng)絡(luò)連接權(quán)值和閾值的隨機(jī)初始化賦值，使得網(wǎng)絡(luò)易陷入局部極值點(diǎn),，影響非線性學(xué)習(xí)能力,，也即預(yù)測(cè)的精度；二是BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的確定,，隱含層節(jié)點(diǎn)數(shù)沒有確切的公式,，選取不當(dāng)易發(fā)生過擬合或?qū)W習(xí)能力不足[6-7]，影響網(wǎng)絡(luò)的泛化能力,。近年來人工智能算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的方法在不同領(lǐng)域也有一些應(yīng)用,，如宋國鋒等[8]在改進(jìn)遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)作預(yù)測(cè)的研究中,，利用改進(jìn)的遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)和初始權(quán)重，而遺傳算法有三個(gè)基本算子：選擇,、交叉和變異（算法的編程實(shí)現(xiàn)比較復(fù)雜）,，這三個(gè)算子的參數(shù)選擇大部分依靠經(jīng)驗(yàn)；程軍等[9]在粒子群優(yōu)化神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型中,，利用粒子群算法優(yōu)化BP網(wǎng)絡(luò)權(quán)重參數(shù),，該方法改善了BP網(wǎng)絡(luò)易陷入局部極小值的不足，提高了收斂速度,。粒子群算法具有遺傳算法的大部分優(yōu)點(diǎn),，并且訓(xùn)練操作簡(jiǎn)單，李雪等[10]通過粒子群算法的慣性權(quán)重和加速因子的線性遞減,，實(shí)現(xiàn)粒子的全局搜索與局部搜索之間的平衡,，提高了尋優(yōu)性能。

　　針對(duì)以上不足,，結(jié)合以前學(xué)者的不同研究成果,，提出非線性調(diào)整粒子群速度更新公式中的慣性因子的方法，根據(jù)樣本數(shù)據(jù)源結(jié)構(gòu)確定粒子群參數(shù)的初始化,，用得到的粒子群的最優(yōu)值初始化BP神經(jīng)網(wǎng)絡(luò)的權(quán)重,，建立預(yù)測(cè)模型。

1 BP神經(jīng)網(wǎng)絡(luò)

　　BP神經(jīng)網(wǎng)絡(luò)是一種多層前饋神經(jīng)網(wǎng)絡(luò),，包括輸入信號(hào)前向傳遞和誤差反向傳播兩個(gè)過程,。在結(jié)構(gòu)上一般由輸入層、隱含層,、輸出層三層構(gòu)成,，每一層的神經(jīng)元狀態(tài)只影響下一層神經(jīng)元狀態(tài)，它被廣泛應(yīng)用在各種預(yù)測(cè)模型中,。在BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型中,，網(wǎng)絡(luò)結(jié)構(gòu)一般只需單個(gè)隱含層就能以任意精度逼近任意有理函數(shù)。訓(xùn)練樣本的輸入,、輸出向量的維數(shù)分別決定了網(wǎng)絡(luò)的輸入,、輸出層神經(jīng)節(jié)點(diǎn)個(gè)數(shù)，典型的只有單個(gè)隱含層,、單個(gè)輸出的BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)如圖1所示,。

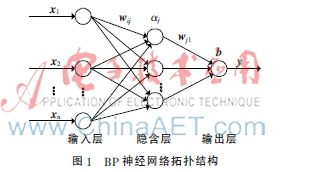
　　圖1中，xi=（x1,，x2,，…，xn）為BP神經(jīng)網(wǎng)絡(luò)的一組輸入向量,，y為網(wǎng)絡(luò)的目標(biāo)輸出值,，wij為輸入層與隱含層之間的連接權(quán)值，wj1為隱含層與輸出層之間的連接權(quán)值,，aj,、b分別為隱含層和輸出層的節(jié)點(diǎn)閾值。若設(shè)隱含層節(jié)點(diǎn)個(gè)數(shù)為m,，則j=1,，2，…,，m,，在前向傳遞中，輸入信號(hào)向量xi從輸入層經(jīng)隱含層逐層傳輸,，最后到輸出層,，通過各層連接權(quán)值矢量、閾值矢量和每一層相應(yīng)的激勵(lì)函數(shù)進(jìn)行計(jì)算,，得出輸出層的預(yù)測(cè)輸出值Y,，若預(yù)測(cè)值Y與目標(biāo)值y之間有誤差，則誤差部分轉(zhuǎn)入反向逐層傳遞,，沿誤差減小方向調(diào)整網(wǎng)絡(luò)各層連接的權(quán)值,、閾值。反復(fù)執(zhí)行以上過程,，使得BP神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)值不斷逼近實(shí)際輸出值,。

2 粒子群優(yōu)化BP神經(jīng)網(wǎng)絡(luò)

　　2.1 基本PSO算法

　　粒子群算法（Particle Swarm Optimization，PSO）是于1995年由Kennedy和Eberhart首次提出的一種群體智能優(yōu)化算法,，該算法的實(shí)現(xiàn)方法簡(jiǎn)單,，被廣泛應(yīng)用在許多優(yōu)化問題中。

　　假設(shè)粒子群規(guī)模為M,，該種群在給定的一個(gè)N維的搜索空間中組成一個(gè)種群T=（X1,，X2，…,，XM）,，粒子i在N維空間中的位置可表示為Xi=（xi1，xi2,，…,，xiN），速度表示為Vi=（vi1,，vi2,，…，viN）,，其中i=1,，2,，…，M,。粒子i在尋找最優(yōu)解的過程中第k次迭代時(shí)經(jīng)過的最好位置記為Pik,，群體在k時(shí)刻經(jīng)過的最好位置記為Pgk，那么每次尋優(yōu)迭代過程中,，粒子i按式（1）來更新自己的速度和位置：

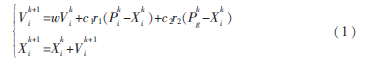
　　式中,，k是迭代次數(shù)；c1為調(diào)節(jié)粒子向自身最優(yōu)位置方向移動(dòng)的步長(zhǎng),，c2為調(diào)節(jié)粒子向全局最優(yōu)位置方向移動(dòng)的步長(zhǎng),，它們是兩個(gè)非負(fù)加速因子；r1和r2為位于[0,，1]之間的常數(shù),。在粒子群算法中，為了控制Vik和Xik的各個(gè)分量在合理區(qū)域內(nèi),，指定Vmax,、Xmax，則Vi∈[-Vmax,，Vmax],，Xi∈[-Xmax，Xmax],，一般會(huì)對(duì)速度向量進(jìn)行最值限制,，當(dāng)Vi≥Vmax時(shí)，取Vi=Vmax,；當(dāng)Vi≤-Vmax時(shí),，取Vi=-Vmax。

　　2.2 改進(jìn)PSO算法

　　基本粒子群算法有容易陷入局部最優(yōu)和收斂精度差的不足,，使得該算法的優(yōu)化效果無法達(dá)到最佳,。研究表明粒子的慣性因子w對(duì)算法的性能影響很大，w較大時(shí)有利于算法的全局搜索,，而w較小時(shí)有利于算法的局部搜索,。因此，選擇一個(gè)合適的慣性權(quán)重很重要,。有學(xué)者提出隨著算法的迭代,，w線性減小的方法，其表達(dá)式為：

　　w（k）=wmax-（wmax-wmin）（Tmax-k）/Tmax（2）

　　式中wmin為最小慣性權(quán)重,，wmax為最大慣性權(quán)重,，Tmax為粒子的最大迭代次數(shù)，k為當(dāng)前迭代次數(shù),。其中,，      0.1≤wmin≤wmax≤0.9,，一般情況下，wmin=0.4,、wmax=0.9時(shí)算法性能最好,。

　　這種方法中w的變化與迭代次數(shù)是線性相關(guān)的，會(huì)使得算法不能很好地解決復(fù)雜的,、非線性變化的優(yōu)化問題。通過分析基本粒子群算法知,，若線性調(diào)整粒子群的慣性因子,，粒子局部搜索和全局搜索性能將有所下降。為解決線性遞減方法調(diào)整的不足,，這里采用非線性方法進(jìn)行調(diào)整,，此時(shí)的慣性因子表達(dá)式為：

　　w（k）=wmin+（wmax-wmin）exp（-25 k/Tmax）（3）

　　2.3 改進(jìn)PSO-BP的算法實(shí)現(xiàn)

　　粒子群優(yōu)化BP神經(jīng)網(wǎng)絡(luò)，首先要確定網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu),，根據(jù)網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)確定粒子的長(zhǎng)度,，即粒子搜索空間的維數(shù)。其次,，BP網(wǎng)絡(luò)中權(quán)值和閾值的調(diào)整是以誤差均方值為基準(zhǔn)的,，以粒子群優(yōu)化的適應(yīng)度函數(shù)作為BP網(wǎng)絡(luò)誤差的反傳函數(shù)，建立誤差均方值與粒子群算法適應(yīng)度函數(shù)的對(duì)等關(guān)系,，這樣目標(biāo)函數(shù)表達(dá)式：

　　式中,，N表示訓(xùn)練樣本總數(shù)，fi表示目標(biāo)函數(shù)的誤差平方和,，y（k）,、ym（k）分別表示目標(biāo)函數(shù)的目標(biāo)輸出值和實(shí)際輸出值。

　　改進(jìn)粒子群算法的尋優(yōu),，具體步驟如下：

　?。?）初始化粒子群參數(shù)：最大迭代次數(shù)Tmax、學(xué)習(xí)因子c1和c2,、粒子群規(guī)模M,、慣性權(quán)重wmax和wmin，在指定的位置與速度范圍內(nèi)隨機(jī)初始化位置向量和速度向量,。

　?。?）初始化BP神經(jīng)網(wǎng)絡(luò)，根據(jù)實(shí)際預(yù)測(cè)的問題確定BP神經(jīng)網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu),，建立網(wǎng)絡(luò)模型,，并根據(jù)網(wǎng)絡(luò)的結(jié)構(gòu)確定粒子的維度。

　?。?）輸入網(wǎng)絡(luò)的訓(xùn)練樣本,，將初始化的位置向量作為當(dāng)前的全局最優(yōu)值映射到網(wǎng)絡(luò)的權(quán)值和閾值中,，計(jì)算期望輸出與實(shí)際輸出的誤差均方，并把它作為粒子群的適應(yīng)度函數(shù),。

　?。?）根據(jù)粒子群速度、位置和慣性因子的改進(jìn)公式,，更新粒子的速度和位置,。

　　（5）迭代運(yùn)算,，確定每個(gè)粒子的個(gè)體極值和全局極值：粒子i的適應(yīng)度值fi與個(gè)體最優(yōu)值pbest比較,，如果小于pbest則取代它作為當(dāng)前的個(gè)體最優(yōu)；適應(yīng)度值fi與全局極值gbest比較,，如果小于gbest則取代它作為當(dāng)前的全局最優(yōu),。

　　（6）算法迭代停止時(shí),，將全局最優(yōu)粒子位置映射到BP神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值中,，作為BP網(wǎng)絡(luò)權(quán)重值。

　?。?）將樣本數(shù)據(jù)源中訓(xùn)練樣本輸入到已確定的網(wǎng)絡(luò)模型中進(jìn)行訓(xùn)練,，用測(cè)試樣本作預(yù)測(cè)。

3 改進(jìn)的PSO-BP旅游客流量的預(yù)測(cè)

　　實(shí)驗(yàn)在MATLAB R2010b平臺(tái)中編程實(shí)現(xiàn),。

　　3.1 數(shù)據(jù)集選定及預(yù)處理

　　實(shí)驗(yàn)數(shù)據(jù)為自貢燈會(huì)在每年的2~3月持續(xù)一個(gè)月左右的每日客流量及其他相關(guān)數(shù)據(jù),。通過燈會(huì)官方網(wǎng)站的電子商務(wù)訂票系統(tǒng)、景點(diǎn)入口的電子紅外掃描,、窗口售票點(diǎn),、自貢氣象局等方式，獲取到的數(shù)據(jù)源參數(shù)有：昨日客流量x1,、去年同期日客流量x2,、窗口售票量x3、電子網(wǎng)站訂票數(shù)量x4,，天氣信息w和周末假日h,，通過這些參數(shù)預(yù)測(cè)目標(biāo)值當(dāng)日客流量y。

　　鑒于神經(jīng)網(wǎng)絡(luò)只能處理表示數(shù)值的輸入數(shù)據(jù),，天氣和周末假日是非數(shù)值量,，并且其他影響因素不是同一量綱，在這里對(duì)不同天氣狀況和周末節(jié)假日等信息作如下變換：

　?。?）經(jīng)分析在2~3月份燈會(huì)期間,，自貢天氣以陰天、多云天氣為主，在此對(duì)天氣信息作如下變換：

　?。?）分析發(fā)現(xiàn),，一周中周五、六,、日三天觀展人數(shù)較其余四天多,，而周一至周四的游客人數(shù)基本接近，波動(dòng)較小,。周末假日信息作如下變換：

　　由于原始數(shù)據(jù)之間的數(shù)值相差較大,，為了提高預(yù)測(cè)精確度，需要對(duì)原始數(shù)據(jù)進(jìn)行歸一化處理,。歸一化的方法很多,，這里通過式（5）來處理：

　　其中，i=1,，2，3,，4,；xmax表示數(shù)據(jù)集里的最大值，xmin表示數(shù)據(jù)集里的最小值,。

　　3.2 實(shí)驗(yàn)仿真

　　以自貢燈會(huì)2009~2013年2~3月份的150組數(shù)據(jù)為訓(xùn)練數(shù)據(jù)集,，以2014年2~3月份的30組數(shù)據(jù)為測(cè)試集，分別用來訓(xùn)練和測(cè)試網(wǎng)絡(luò)模型,，整個(gè)輸入向量為6×180的矩陣,。

　　改進(jìn)PSO優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的初始參數(shù)確定：種群規(guī)模M=50，最大迭代次數(shù)G=200,，輸入節(jié)點(diǎn)數(shù)為6,，輸出節(jié)點(diǎn)數(shù)為1，隱含層節(jié)點(diǎn)個(gè)數(shù)取為15,，共有6×15+15×1=105個(gè)權(quán)值,，15+1=16個(gè)閾值，搜索空間維數(shù)N=105+16=121,。建立6-15-1結(jié)構(gòu)的BP網(wǎng)絡(luò),。同時(shí)訓(xùn)練BP、PSO-BP預(yù)測(cè)模型,，使用這三種模型對(duì)測(cè)試集進(jìn)行預(yù)測(cè),，對(duì)比預(yù)測(cè)結(jié)果并作性能分析。

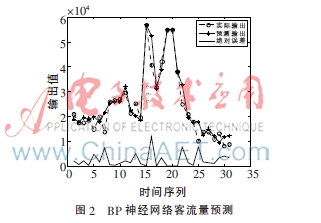
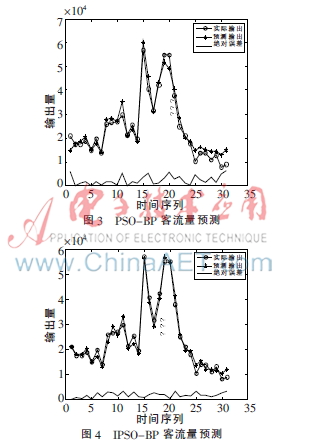
　　BP網(wǎng)絡(luò)使用最小梯度下降法作為訓(xùn)練函數(shù),，目標(biāo)誤差精度為10-4,；在標(biāo)準(zhǔn)PSO-BP中，加速因子選擇c1=c2=2.0，其他參數(shù)選擇與改進(jìn)的PSO-BP網(wǎng)絡(luò)的參數(shù)相同,。圖2,、3、4分別為BP,、PSO-BP,、IPSO-BP當(dāng)日預(yù)測(cè)客流量與實(shí)際人數(shù)的擬合圖，并給出了兩者的絕對(duì)誤差曲線,，其中橫軸時(shí)間序列表示2~3月的時(shí)間量（每天）,，縱軸表示對(duì)應(yīng)每天的景區(qū)客流量人數(shù)。

　　比較圖2,、3,、4可知，利用慣性因子的非線性遞減方法,，預(yù)測(cè)曲線擬合度較高,，預(yù)測(cè)的絕對(duì)誤差明顯減小。此時(shí)BP神經(jīng)網(wǎng)絡(luò),、PSO-BP神經(jīng)網(wǎng)絡(luò)和IPSO-BP神經(jīng)網(wǎng)絡(luò)的均方誤差分別是：mseBP=1.4×10-3,，msePSO-BP=4.76×10-4，mseIPSO-BP=3.42×10-4,，可以看出改進(jìn)后的預(yù)測(cè)精度有所提高,。

4 結(jié)束語

　　本文提出改進(jìn)的PSO-BP算法建立預(yù)測(cè)模型，并以自貢燈會(huì)客流量為例做預(yù)測(cè)分析,。雖然選用的訓(xùn)練樣本數(shù)據(jù)并不多,，但從仿真結(jié)果看，卻取得了較高精度的預(yù)測(cè)效果,，說明粒子群算法無需過多原始數(shù)據(jù)也能得到理想的尋優(yōu)結(jié)果,。改進(jìn)PSO和BP網(wǎng)絡(luò)組合的預(yù)測(cè)模型簡(jiǎn)單有效，對(duì)自貢燈會(huì)的管理決策有較大的參考價(jià)值,。如何進(jìn)一步提高算法在法定節(jié)假日,、異常天氣情況下的客流量預(yù)測(cè)的泛化能力，是下一步研究的重點(diǎn),。

　　參考文獻(xiàn)

　　[1] 陶偉,，倪明．中西方旅游需求預(yù)測(cè)對(duì)比研究：理論基礎(chǔ)與模型[J]．旅游學(xué)刊，2010,，25（8）：12-17．

　　[2] SMERAL E,， WITT S F， WITT C A． Econometric forecasts： tourism trends to 2000[J]． Annals of Tourism Research,，1992,，19（3）：450-466．

　　[3] 陳萍萍．基于時(shí)間序列的旅游需求預(yù)測(cè)模型[J]．統(tǒng)計(jì)與決策,，2013（18）：11-13．

　　[4] 趙娟，江立輝．旅游客流量預(yù)測(cè)的模糊時(shí)間序列模型以黃山風(fēng)景區(qū)為例[J]．合肥學(xué)院學(xué)報(bào)（自然科學(xué)版）,，2014,，24（4）：26-31．

　　[5] ZENG Z L， ZHENG Y． The grey model and its application to forecast of inbound visitors from mainland China to Macau[C]． 3rd Intrmational Conference on Management Science and Engineering Management,， 2009：48-54．

　　[6] 李松,，劉力軍，翟曼．改進(jìn)粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的短時(shí)交通流預(yù)測(cè)[J]．系統(tǒng)工程理論與實(shí)踐,，2012,，32（9）：2045-2049．

　　[7] 王德明，王莉,，張廣明．基于遺傳BP神經(jīng)網(wǎng)絡(luò)的短期風(fēng)速預(yù)測(cè)模型[J]．浙江大學(xué)學(xué)報(bào)（工學(xué)版）,，2012，46（5）：837-841．

　　[8] 宋國鋒,，梁昌勇,，梁焱，等．改進(jìn)遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的旅游景區(qū)日客流量預(yù)測(cè)[J]．小型微型計(jì)算機(jī)系統(tǒng),，2014,，35（9）：2136-2141．

　　[9] 程軍，李榮鈞．基于粒子群優(yōu)化的神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型[J]．教學(xué)的實(shí)踐與認(rèn)識(shí),，2015，45（3）：176-180．

　　[10] 李雪,，顧沈明,，年浩．改進(jìn)粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的糧食產(chǎn)量預(yù)測(cè)[J]．漳州師范學(xué)院學(xué)報(bào)（自然科學(xué)版），2014,，27（1）：56-61．