摘  要： 織物瑕疵紋理特征復雜,，單一特征不能很好地反映紋理信息,。為此，本文提出一種基于局部二進制模式（Local Binary Pattern,，LBP）算子和灰度共生矩陣（Gray Level Co-occurrence Matrix,，GLCM）的多特征融合算法。首先,，對LBP算子進行了改進,，提出一種基于鄰域像素中值的中心對稱LBP算子；然后,，將其提取出的紋理特征和灰度共生矩陣提取的紋理特征進行融合,；最后，通過極速學習機和支持向量機做分類實驗,，驗證融合特征描述織物瑕疵紋理特征的能力,。實驗表明，本文方法提高了織物物疵點檢測率,，并且具有很好的抗干擾能力,。

　　關(guān)鍵詞： 紋理特征,；中心對稱二進制模式,；灰度共生矩陣；特征融合

0 引言

　　織物的疵點檢測是紡織品質(zhì)量檢測的重要環(huán)節(jié),。傳統(tǒng)基于人工的檢測,，存在主觀因素大、不能滿足市場發(fā)展要求等問題,。近年來,，針對計算機視覺的疵點自動檢測的研究成為熱點。紋理在圖像中普遍存在,，所以成為一種重要的研究線索,。目前，常用的紋理特征提取算法主要可以分為四大類：結(jié)構(gòu)分析方法、統(tǒng)計方法,、紋理模型方法和信號處理方法[1],。其中，灰度共生矩陣（Gray-Leve Co-occurrence Matrix,，GLCM）是基于統(tǒng)計的紋理分析方法,，應用最為廣泛[2]。但是該算法是從整體上描述紋理特征信息,。局部二進制模式（Local Binary Pattern,，LBP）可以很好地描述紋理的局部特征信息，LBP有很多的衍生算子,，參考文獻[3]中提出的帶有門限噪聲的中心對稱局部二進制模式（Center-Symmetric Local Binary Pattern,，CS_LBP）就是其中的一種。CS_LBP雖然能夠?qū)D形進行降維并具有旋轉(zhuǎn)不變性和較好的噪聲門限,，但是對噪聲的抗干擾性能不足,。為此，本文提出一種基于鄰域像素中間值的中心對稱MCS_LBP算子,，并與灰度共生矩陣提取的4個特征量（對比度,、相關(guān)性、能量,、熵）進行特征融合,，提高對光照等因素抗干擾能力和算法的魯棒性。

　　最后通過ELM（Extreme Learning Machine）和SVM（Support Vector Machine）對提取的特征進行分類處理,，通過分類的精確度,，驗證本文算法提取的融合特征對織物瑕疵紋理特征描述的檢測能力。本文設計的織物疵點檢測系統(tǒng)的結(jié)構(gòu)如圖1所示,。

1 織物瑕疵紋理特征提取

　　1.1 灰度共生矩陣

　　灰度共生矩陣由Haralick在1973年首先提出[2],。矩陣是由圖像灰度級之間的聯(lián)合概率密度構(gòu)成的，是從統(tǒng)計的角度反映圖像中任意兩點間灰度的空間相關(guān)性,。如下式：

　　[P（i,，j，d,，]L×L（1）

　　其中,，為定義的方向，取值為0°,，45°,，90°，135°四個方向,；d為間距,；i,，j分別表示i行，j列,；L是指矩陣的維數(shù),。熵（H）、相關(guān)性（C）,、能量（E）,、對比度（I）的定義表達式如下：

　　1.2 LBP算子

　　LBP算子是從局部近鄰定義中衍生出來的。具有灰度不變性,、旋轉(zhuǎn)不變性,、對光照變化不敏感、計算快速簡單等優(yōu)點,，在圖像處理方面被廣泛使用[4],。傳統(tǒng)的LBP算子為圖像的每個像素定義了一個以該像素為中心的3×3窗口（紋理單元），然后以此中心像素的灰度值為閾值,，對窗口的其余8個像素進行二值化,，然后根據(jù)像素的位置和二值化的結(jié)果進行加權(quán)求和，得到該像素的LBP值,，具體的公式如下：

　　其中：

　　V（pi-pc）=1,，pi-pc≥00，pi-pc<0（7）

　　其中,，（xc,，yc）為8鄰域的中心像素C的坐標，像素值為pc,，i為鄰域像素,，像素值為pi，R為鄰域半徑,，以像素為單位,，Ｎ表示以R為半徑的圓周鄰域上像素個數(shù)。LBP算子的示意圖如圖2,。

　　由公式（6）,、（7）得出：LBP=（00111100），換算成十進制為60,。

　　傳統(tǒng)的LBP特征在進行直方圖統(tǒng)計時數(shù)量多而且具有較多的冗余,，其衍生算子即帶有門限噪聲的CS_LBP算子（Center Symme-tric Local Binary Pattern）[5-6]具有很好的統(tǒng)計特性,，同時具有中心對稱特性,。如圖3所示，以gc為中心,，按順時針將兩個對稱像素的灰度值進行比較,，能夠得到只有16維的直方圖,，對LBP起到降維的作用。CS_LBP算子的計算如式（8）,，計算的方法類似于LBP算子,。

　　但實際應用中發(fā)現(xiàn)，CS_LBP雖然具有對圖形進行降維,、旋轉(zhuǎn)不變性和噪聲門限的優(yōu)點,，但對光照等抗干擾能力有所欠缺。為此,，本文提出基于鄰域像素中間值的中心對稱的MCS_LBP算子,。基于鄰域像素中值的LBP算子公式如下：

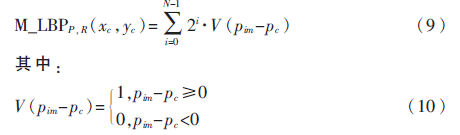
　　鄰域中間值的概念如下：

　　鄰域周圍的像素點按照像素值從大到小的順序排列,，下標記作1,，2，…n,，即對于有限序列{x1,，x2，…xn}的中值定義如下：

　　基于鄰域像素中值的算法對鄰域像素灰度值進行排序,，減少了光照,、噪聲等因素引起的局部像素值的突變。

　　綜上所述,，本文提出一種新的局部紋理算子——MCS_LBP（Median Center Symmetric Local Binary Pattern）,，綜合公式（8）和公式（9），得：

　　MCS_LBPP,，R=（M_LBPP,，R，CS_LBPP,，R）（12）

　　2 特征融合算法

　　織物瑕疵紋理特征復雜,，單一特征不能很好地反映紋理信息。首先,，將灰度共生矩陣提取的反應織物紋理信息的能量,、熵、對比度,、相關(guān)性4個特征和本文改進的MCS_LBP算子提取的局部紋理特征進行融合,。由于特征向量維數(shù)較大，所以在進行特征融合之前,，需要對融合的特征進行主成分分析（Principal Component Analysis,，PCA）[7]，這樣可消除特征間的冗余信息,，降低特征空間維數(shù),。本文引用一種權(quán)重因子來進行特征融合[8],，模型如下式：

　　其中，N表示描述每一種類別的特征總數(shù),，cj表示類別,，ati為特征ti的權(quán)重，d表示待分對象,。

　　原理：對Ｎ個特征,，單獨用每一個特征分類，得到Ｎ組概率值,。按照各項特征對于分類的重要度,，可對這Ｎ組概率值加權(quán)求和，得到各個類別最終的分類準確率,。

　　關(guān)于權(quán)重的估計,，本文采用參考文獻[8]中的方法進行處理。用一個分類器訓練不同特征的權(quán)重,。將單獨使用特征ti分類的結(jié)果表示為向量Pti=（Pi1,，Pi2，…,，PiN）,，i=1，2,，…N,。Pij表示用特征ti分類后類別cj的分類準確率，由此可得到N個特征分類后的結(jié)果,，可以用矩陣P=（Pi1,，Pi2，…,，PiN）表示,，由公式（13）可得到分類準確率的方程組：

　　其中，a=（at1,，at2,，…，atN）表示待求的各特征的權(quán)重,。P為特征分類準確率矩陣,，矩陣元素為各項的分類準確率。f表示累加后的各個類別的分類準確率,，在權(quán)重訓練時,，已經(jīng)對類別進行了人工標注。仿照參考文獻[8]的方法將其他類別加入了松弛變量，防止出現(xiàn)過擬合的情況,。

　　這樣對于M個訓練樣本求解平均,，從而得到最終的特征權(quán)重：

3 織物疵點檢測的應用

　　織物紋理的種類繁多,，但隨著技術(shù)的進步,，目前實際生產(chǎn)中常見的疵點主要有圖3所示的8種，本文主要針對8種平紋織物瑕疵圖像進行分類,。圖3展示了常見的疵點外形特征,。

　　具體實驗如下：每種疵點選取圖片50張，其中25張作為訓練樣本,，剩余的25張作為測試樣本,。首先進行樣本預處理，主要是同態(tài)濾波,、直方圖均衡化等處理,，處理后的圖像如圖4所示。然后通過CS_LBP,、M_LBP,、本文的方法進行特征提取，接下來是主成分分析和特征融合,，為分類器訓練準備,。

　　在分類器的設計上，為了更好地顯示分類效果,，驗證本文方法的合理性,，本文選擇支持向量機和極速學習機兩種分類算法。主要是因為基于SVM的織物疵點檢測的研究相對較為成熟,，已取得一些較好的實驗成果,，如參考文獻[10，12]中均取得較好的分類結(jié)果,。另一方面由黃廣斌等[9,，11]提出的ELM是一種基于單隱層前饋神經(jīng)網(wǎng)絡（Single-hidden Laye-er Feedforward Network，SLFN）的極速學習算法,。其最大的特點是：訓練速度快于現(xiàn)存的任何一種遞歸學習算法[13],。只需要設置網(wǎng)絡的隱層節(jié)點數(shù)，然后對輸入權(quán)值和隱層偏置隨機賦值,，最后通過最小二乘法經(jīng)一次矩陣運算即可得到輸出權(quán)值,，無需迭代。由于目前市場上對織物疵點檢測的實時性要求越來越高,，而織物疵點檢測算法的實時性相對不足,，本文將此分類算法應用到織物的疵點檢測中具有一定的現(xiàn)實意義。

　　另外為了更好地說明實驗結(jié)果,，本文在分類器設計時采用一對一的方式,。這種方法主要是每兩類間設計一個分類器,。對一個測試樣本進行分類時，每一個分類器都對其進行判斷并輸出類別,，取次數(shù)多的為樣本類別,。依此方法，本文8類織物疵點共需28個分類器,，即：

　　ELM12,，ELM13，ELM14,，ELM15,，ELM16，ELM17,，ELM18,，LM23，LM24,，LM25,，LM26，LM27,，LM28,，LM34，ELM35,，ELM36,，ELM37，ELM38,，ELM45,，ELM46，ELM47,，ELM48,，ELM56，ELM57,，ELM58,，ELM67，ELM68,，EILM78,。

　　實驗時分別取兩類樣本中的25張作為訓練樣本。分類器訓練好以后,，對測試樣本進行分類實驗,，并對ELM算法循環(huán)50次進行改進，得到訓練和測試時間，分類的準確率數(shù)據(jù)是經(jīng)過50次隨機實驗后的平均值,。對SVM的處理類似,，不再贅述。各種方法提取的特征分類的結(jié)果如表1,、2,、3所示。

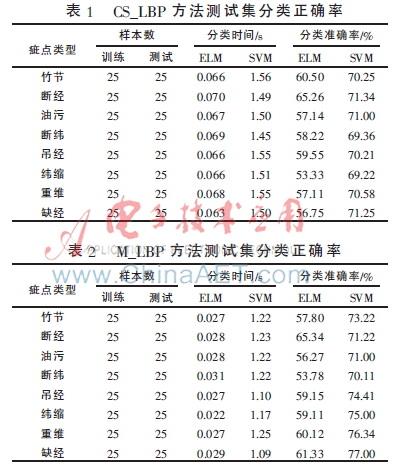
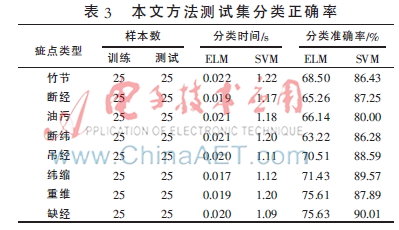
　　通過上述的實驗結(jié)果表明：（1）基于本文算法的分類的準確率最高,，間接地說明了本文提出的算法所提取的織物紋理特征可以更好地描述織物瑕疵紋理,，驗證了本文算法的合理性,。（2）本文方法與M_LBP和CS_LBP對比,，分類的準確率得到了提高，說明了融合基于鄰域像素的中值后,，減少了光照等外因造成圖像局部突變的干擾,，算法的魯棒性得到提高。（3）本文算法時間上也得到了降低,，也說明了特征融合時采用PCA降維的有效性,。

4 結(jié)束語

　　本文提出基于鄰域像素中值的中心對稱的MCS_LBP算子，并與灰度共生矩陣提取的能量,、熵,、對比度、相關(guān)性特征進行了特征融合,。在特征融合時,，引入了一種基于權(quán)重因子的特征融合方法。通過兩種分類算法進行分類實驗,，結(jié)果表明本文方法提高了分類的準確率,，同時魯棒性得到提高，說明融合的特征描述紋理的能力得到了增強,。多特征融合是特征提取的一個研究熱點和難點,，如何更好地選取多種特征進行特征融合和構(gòu)造性能優(yōu)良的特征融合算法應該是下一步研究的方向。另外,，通過比較兩種分類算法的結(jié)果可見,，ELM算法雖然分類的速度很快，但分類的準確率很低,，對其進行改進,，提高其準確率，并應用于織物的疵點檢測是一個研究方向,。

參考文獻

　　[1] 謝菲,，陳雷霆，邱航.基于紋理特征提取的圖像分類方法研究及系統(tǒng)實現(xiàn)[J].計算機應用研究，2009,，26（7）：2767-2770.

　　[2] 龔家強,，李曉寧.基于共生矩陣紋理特征提取的改進算法[J].計算機工程與設計，2011,，32（6）：2068-2071.

　　[3] 劉丹,，胡永健，劉斐貝.聯(lián)合SIFT特征點和CS_LBP特征描述子的復制粘貼篡改檢測[J].合肥工業(yè)大學學報,，2012,，35（3）：1003-5060.

　　[4] HADID A， ZHAO G,， AHONEN T,， et al. Face analysis using local binary patterns[Z]. Handbook of Texture Analysis， 2008.

　　[5] 向斌,，陳曉云.基于方向?qū)?shù)紋理描述子的紋理圖像聚類[J].微型機與應用,，2013，32（19）：37-40.

　　[6] HEIKKILA M,， PIETIKAINEN M,， SCHMID C. Description of interest regions with local binarypatterns[J]. Pattern Recognition， 2009,，42（3）：425-436.

　　[7] 趙廣社,，張希仁.基于主成分分析的支持向量機分類方法研究[J].計算機工程與應用，2004,，40（3）：37-38.

　　[8] 麥林,，俞能海.多特征融合的博客文章分類方法[J].小型微型計算機系統(tǒng)，2010,，31（6）：1000-1220.

　　[9] HUANG G B,， ZHU Q Y， SIEW C K. Extreme learning machine： theory and applications[J]. Neurocomputing,， 2006,，70（1）：489-501.

　　[10] 付蓉，石美紅.基于自適應LBP和SVM的織物疵點檢測算法[J].計算機應用,，2010,，30（6）：1597-1601.

　　[11] HUANG G B， CHEN L. Enhanced random search based incremental extreme learning machine[J]. Neurocomputing,，2008,，71（16）：3460-3468.

　　[12] 趙靜，高偉,，歐付娜,，等.基于小波特征SVM的織物疵點識別[J].紡織科技進展,，2012（2）：49-52.

　　[13] HAYKIN S. Neural network and learning mach-ines[M]. New York： Prentice Hall， 2009.