摘  要： 針對具有豐富紋理細節(jié)的圖像的增強,，本文提出了一種基于小波低頻自適應分層的算法。該算法根據(jù)圖像小波分解的低頻部分計算出相應的對比度信息,，以實現(xiàn)自適應分層,，然后依據(jù)分層的結(jié)果確定自適應增強函數(shù)，最后達到不同程度的增強效果,。通過實際的實驗表明,，所提出的基于小波分解的分層自適應增強算法對具有豐富紋理細節(jié)的圖片具有較好的增強效果，能夠有效地提高圖像質(zhì)量,。

　　關(guān)鍵詞： 圖像增強,；小波變換,；自適應增強；分層增強

0 引言

　　圖像的對比度是一幅圖像明暗之間不同對比度層級的測量,，代表著一幅圖像灰度反差的大小,。一般在對圖像信息的分析過程中，圖像對比度的強弱將直接影響信息提取的難易程度,。正是針對圖像的這一特點,，學者們提出了很多增強圖像的算法。在空域上有直方圖均衡化等經(jīng)典方法,，而在頻域上有基于傅里葉變換,、小波變換等的經(jīng)典方法。同時為提高圖像的增強效果,，在原始小波的基礎上又提出了緊支撐二維小波多尺度小波[1-5],，并拓展出基于多尺度Retinex算法的圖像增強[6]。

　　這些方法均將圖像的所有成分進行處理,，對圖像的邊緣等銳利的部分造成了一定的畸變,，從而對圖像造成了一定程度的失真。并且,，針對細節(jié)豐富的圖像,，例如遙感圖像等，這些方法會嚴重影響到圖像的細節(jié)準確性,。針對這一情況,，提出了一種新的變換方法——Contourlet變換[7-8]，這一變換在圖像處理的過程中能夠較好地考慮圖像的細節(jié)信息,。參考文獻[9]提出了一種基于Contourlet變換的圖像增強算法,，它在對圖像增強的同時又在一定程度上對圖像的細節(jié)進行了處理。但是,，其對于圖像細節(jié)的凝結(jié)度不高,。

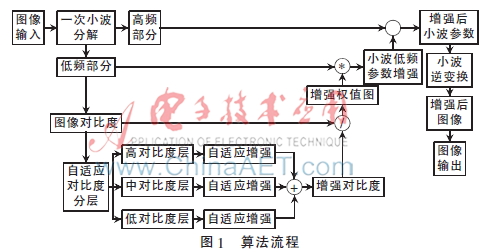
　　針對這一問題，本文提出了一種基于小波分解的層次化的自適應圖像增強算法,。它能有效地克服上述在增強過程中產(chǎn)生的問題,。算法具體流程如圖1所示。首先,，通過小波變化可以得到將要處理的低頻信息,。然后，通過計算低頻部分的局部平均對比度可以得到圖像的對比度信息,。再次，通過自適應的方式,，計算出不同對比度強度像素的調(diào)整系數(shù),。最后,，利用調(diào)整后的低頻信息進行小波的逆變換得到處理后的圖像。

1 圖像的小波分解

　　小波變換和Fourier變換一樣,，是一種數(shù)學變換,。它之所以能夠?qū)π盘栠M行多尺度細化，最終達到高頻處時間細分,，低頻處頻率細分,，是由于它具有一個特殊的變換核，即小波函數(shù),。

　　圖像的二維小波變換,，實質(zhì)上就是對圖像進行二維離散小波變化。離散小波變換可以將圖像分解為LL,、LH,、HL、HH四個不同的頻率子帶,。它們分別代表了圖像的高頻低頻,，以及兩個對角線的小波能量分布。圖像的主要能量集中在小波的LL子帶上,，而且它的三個子帶則主要包含了圖像的邊緣信息,。如圖2所示。

2 小波分層自適應增強算法實現(xiàn)

　　2.1 低頻子帶對比度計算

　　通過離散小波對圖像的分解,，可以得到圖像的小波低頻分量,，即小波的LL層。而圖像的對比度是指一幅圖像中明暗區(qū)域最亮的白和最暗的黑之間不同亮度層級的測量,，差異范圍越大代表對比越大,，反之，差異范圍越小代表對比越小,。為方便估計圖像的對比度，在這里定義一個針對描述圖像像素級對比度的數(shù)值C（p）,，其定義如下：

　　其中,，?贅-{p}表示圖像區(qū)域?贅中去除p以外的像素點；|I（p）-I（j）|為像素點p與j之間的灰度絕對差值,，用于模仿視覺系統(tǒng)的側(cè)抑制性,；d（·）是兩點間的歐式距離,，其值將作為控制j點對p點影響的權(quán)重,。利用C（p）,，可以計算圖像局部區(qū)域的對比度。而在實際的計算中一般取3×3大小的區(qū)域作為計算的最小單位,。如圖3所示。

　　由C（p）的定義可以知道,，對于純色的圖像（即I（j）等于一個恒定值），其C（p）的值恒等于0,。

　　通過不同尺寸的窗口,，可以得到圖像在不同對比區(qū)域下的像素級的對比度值,。圖3（b）顯示了選用3×3大小的窗口下對比度的分布情況。

　　2.2 低頻子帶對比度分層

　　通過上一步的計算,，可以得到代表每一個像素點的對比度強度值。那么接下來對這一強度值進行不同程度的增強,。

　　由于圖像的對比度集中反映了圖像的像素亮度的強度分布差異,，而一般的對比度處理是將圖像的灰度值直接進行線性映射,，這從一定程度上減弱了這種強度分布差異，導致圖像的部分細節(jié)被模糊,。針對這種現(xiàn)象，考慮對圖像的對比度進行分層處理,。即,，利于多閾值的方式,，將圖像的對比度進行分層，并且對不同的分層采取不同的增強方式,。

　　在這里，將對比度分布圖的均值Av作為主要參數(shù)來確定閾值,。

　　同時,，針對人視覺對圖像對比度感知的特點,，可以定義雙閾值分別為Tl=0.7Av,，Th=1.7Av。

　　利用這兩個閾值可以將對比度數(shù)據(jù)分成不同的三層,，即低值子帶、中值子帶,、高值子帶,。同時,，由于對比度分布圖是針對小波低頻帶的像素級的對比度計算，因此在進行分層之前,，應該對分布圖進行適當?shù)母咚篂V波處理，以避免分層后各層值分布過分獨立而出現(xiàn)單點現(xiàn)象,。

　　通過將對比度分布圖進行雙閾值分層，可以得到如圖4（b）,、（c）,、（d）所示的三個子帶（重映射到[0,，255]），它們代表著不同值的像素級對比度的集合,。

　　2.3 分層增強函數(shù)的確定

　　在進行分層對比度增強之前,，應該考慮圖像整個場景的平均亮度,，以便為分層對比度增強提供更多的圖像信息。

　　本文利用對數(shù)平均亮度I作為圖像整個場景的亮度表征量,。其具體定義如下：

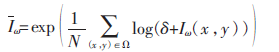
　　其中，I（x,，y）代表像素點（x,，y）的灰度值,，N是場景內(nèi)的像素數(shù)，δ是一個很小的數(shù)用來應對像素點純黑的情況。在這里,，將計算圖像的整體對數(shù)平均亮度,，即代表整幅圖像，而N代表整幅圖像的像素點數(shù),。

　　針對不同的三個層次的對比度增強,，需要確定一個分段式的增強曲線,。為確定這一曲線，本文定義了四個關(guān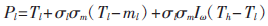)鍵拐點,。即，其中,，Tl表示分層閾值中的低閾值,，Th表示分層閾值中的高閾值,，ml表示低值子帶的均值，l,、m分別表示低值子帶與中值子帶的標準差。

　　其中h為高值子帶的標準差,。

　　通過Pl與Ph這兩個拐點可以得到一條用于分層增強的映射函數(shù)Fs（x）。同時,，為避免增強后產(chǎn)生區(qū)塊效應,，利用Gamma校正的方式對映射函數(shù)Fs（x）進行處理,，得到最終的映射函數(shù)：

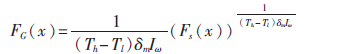
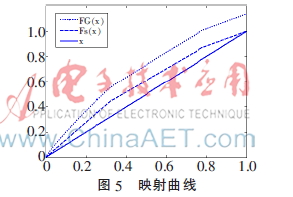
　　通過計算Pl與Ph兩個拐點，可以得到如圖5中所示的映射曲線Fs（x）,，經(jīng)過Gamma校正后，可以得到圖5中的映射曲線FG（x）,。對比FG（x）與直線y=x可以發(fā)現(xiàn),，映射曲線在x<Tl時具有最大的增強趨勢。

　　2.4 增強權(quán)值圖的確定

　　利用得到的分段式映射曲線FG（x）,，可以分別對雙閾值分層得到的三個分層進行處理。通過對三個增強后的子帶求和,，可以得到增強的對比度分布圖。通過對原對比度分布圖和增強后的對比度分布圖的比較,，可以得到每一個像素的實際增強權(quán)值,。即

　　W（p）=FG（C（p））/C（p）

　　這些權(quán)值的集合就是需要的權(quán)值圖W。

　　通過FG（x）的重映射,，可以得到如圖6中（b）、（d）,、（f）三個增強子帶。通過原子帶與增強子帶的比較可以得到權(quán)值集合,。為方便顯示,，這里將權(quán)值圖重映射到了[0,，255]。

　　2.5 小波系數(shù)增強及逆變換

　　利用計算得到的權(quán)值圖W,，對小波分解的低頻子帶LL進行增強處理LLs=W·LL,，從而得到增強后的小波低頻系數(shù)LLs,。最后再經(jīng)過小波的逆變換得到增強后的圖像。

　　通過對比圖7中（a）與（b）可以看出,，相對于原圖,，增強后的圖像細節(jié)完全展現(xiàn)了出來。對比圖7（a）與圖7（b）可以明顯看出原圖模糊的細節(jié)經(jīng)過對比度增強后得到了改善,。

3 實驗對比

　　3.1 圖像增強的評價標準

　　由于圖像增強很大程度上是以人類視覺效果進行衡量的,，因此很難利用定量的參數(shù)對圖像的增強效果進行全面的評價。但是,，在實際處理中,，可以選取一些標志圖像質(zhì)量的重要因素來作為評價的定量指標。這里選取圖像的信息熵以及清晰度,。

　?。?）信息熵

　　圖像的信息熵是圖像所含信息的度量。其值越大，表示圖像所含信息越豐富,。其定義如下：

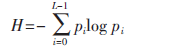
　　其中pi是灰度級為i出現(xiàn)的概率,。L表示圖像的灰度級。

　?。?）清晰度

　　圖像的清晰度可以反映出圖像的微小細節(jié)反差以及紋理變換特征。其值越大,，表示圖像越清晰,。其定義如下：

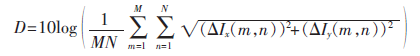
　　其中,，Ix,，Iy分別表示圖像的x與y方向的差分。

　　3.2 圖像增強效果

　　這里利用幾種常見的圖像增強方法：直方圖均衡化,，單一小波,，Contourlet變換以及本文所提出的基于小波分層增強的方法,，同時對相同的圖像進行處理。

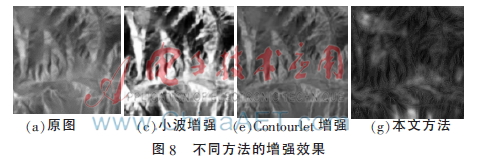
　　如圖8對不同方法的增強效果進行對比,，通過直觀的視覺可以發(fā)現(xiàn)利用小波的增強方式可以較大程度上改變圖像的灰度值分布。而基于Contourlet變換的圖像增強,，可以在不明顯改變圖像灰度值分布的情況下對圖像的細節(jié)有較明顯的增強,。而利用本文的方法對圖像產(chǎn)生了較大的改變,，其增強后雖然圖像整體偏暗，但是其對圖像的細節(jié)產(chǎn)生了很大的改善,。尤其對比局部的圖像細節(jié)，可以很明顯看出通過本文的方法,，圖像的細節(jié)相對于其他方法具有最佳的改善,。對不同方法的增強結(jié)果進行信息熵和清晰度的計算可以得到表1,。

4 結(jié)論

　　針對具有豐富細節(jié)的圖像的特點，本文提出了一種基于小波分解的自適應圖像增強算法。通過對輸入圖像的小波分解,，獲得圖像的小波低頻信息。其次,，依據(jù)所得的小波的低頻帶,，計算得到相應的對比度信息C（p）,。然后，根據(jù)雙閾值的定義,，確定自適應增強函數(shù)FG（x）,，以此計算出最后所需的增強權(quán)值W,。最后，利用W計算出增強后的小波低頻帶,，完成小波的逆變換。這樣使得在對圖像的增強過程中,，有效地改善了圖像的細節(jié)質(zhì)量,。

參考文獻

　　[1] 朱立新,，王平安，夏德深.基于梯度場均衡化的圖像對比度增強[J].計算機輔助設計與圖形學學報,，2007,，12（12）：1546-1552.

　　[2] 董廣杰，林旭梅.小波分析在圖像降噪中的應用[J].微型機與應用,，2013，32（12）：32-34.

　　[3] IBRAHIM H,， KONG N S P. Brightness preserving dynamic histogram equalization for image contrast enhancement[J]. IEEE Trans on Consumer Electronics,， 2007,， 53（4）：1752-1758.

　　[4] 湯仁民,，李國芳,，王代強,，等.基于小波的圖像基本處理技術(shù)研究[J].微型機與應用,，2015,，34（2）：44-46.

　　[5] LEE E， KIM S,， KANG W,， et al. Contrast enhancement using dominant brightness level analysis and adaptive intensity transformation for remote sensing images[J]. IEEE Geoscience And Remote Sensing Letters，2013,，1（10）：62-65.

　　[6] 趙艷飛，高清維,，盧一相.基于多尺度Retinex算法的遙感圖像增強[J].計算機技術(shù)與發(fā)展,，2008，2（18）：70-73.

　　[7] Liu Gang,， Luo Xutao,， Liang Xiaogeng. An adaptive denoising and enhancing algorithm based on the MAP rule in the contourlet domain for infrared image[C]. Computational Intelligence and Software Engineering,， 2009， International Conference on,， 2009：1-5.

　　[8] Jing Fang,， Dong Wang,， Yang Xiao， et al. De-noising of SAR images based on Wavelet-Contourlet domain and PCA[C]. Signal Processing （ICSP）,， 2014 12th International Conference on,， 2014：942-945.

　　[9] 陳志剛，尹福昌.基于Contourlet變換的遙感圖像增強算法[J].光學精密工程,，2008，10（16）：2030-2037.