摘 要: 針對(duì)超寬帶雷達(dá)頻帶分割濾波器不理想、導(dǎo)致子帶脈沖壓縮和直接脈沖壓縮結(jié)果相差較大的問題,本文提出了基于正交鏡像濾波器組的子帶脈沖壓縮方法。首先設(shè)計(jì)了近似完全重建的正交鏡像濾波器組,定義目標(biāo)函數(shù)為通帶誤差、阻帶能量和失真轉(zhuǎn)移函數(shù)平方誤差的加權(quán)和,通過無約束的變尺度方法將其最小化,然后用設(shè)計(jì)的正交鏡像濾波器作為頻帶分割濾波器,實(shí)現(xiàn)子帶脈沖壓縮。仿真結(jié)果表明,本文設(shè)計(jì)的正交鏡像濾波器組,相比現(xiàn)有的設(shè)計(jì),具有更小的峰值重建誤差、通帶和阻帶誤差。提出的子帶脈沖壓縮方法,與傳統(tǒng)方法相比,主副瓣比和主瓣寬度等脈壓性能也明顯提高。
關(guān)鍵詞: 超寬帶雷達(dá);脈沖壓縮;正交鏡像濾波器組;FIR原型濾波器
0 引言
超寬帶雷達(dá)因具有高距離分辨率、低截獲概率以及良好的目標(biāo)識(shí)別能力等優(yōu)點(diǎn),受到國內(nèi)外廣泛關(guān)注。對(duì)大時(shí)寬帶寬積回波信號(hào)進(jìn)行脈沖壓縮可獲得較高的距離分辨率和較遠(yuǎn)的作用距離,但目前受模數(shù)轉(zhuǎn)換器件的限制,還無法直接對(duì)超寬帶信號(hào)進(jìn)行處理[1]。參考文獻(xiàn)[2]提出了基于頻帶分割的多通道綜合脈沖壓縮方法,但由于模擬頻帶分割濾波器組不夠理想,使得通過濾波器后的信號(hào)會(huì)產(chǎn)生混疊以及幅度和相位失真,影響脈沖壓縮的性能。
正交鏡像濾波器組的出現(xiàn),為寬帶信號(hào)的處理提供了有效方法。隨著多抽率數(shù)字信號(hào)的飛速發(fā)展,其作用越來越重要,在圖像編碼、多載波調(diào)制系統(tǒng)[3]、抽樣理論[4]以及寬帶波束形成聲吶等各領(lǐng)域已被廣泛應(yīng)用。對(duì)近似重建正交鏡像濾波器的設(shè)計(jì)方法也有多種,傳統(tǒng)的設(shè)計(jì)方法是采用不同的窗函數(shù)設(shè)計(jì)濾波器,最優(yōu)解的收斂需要多次迭代,每次迭代之后需要重新對(duì)濾波器進(jìn)行設(shè)計(jì),運(yùn)算量較大。參考文獻(xiàn)[5]提出了一種基于線性目標(biāo)函數(shù)的最小加權(quán)二乘方法獲得最優(yōu)濾波器系數(shù),參考文獻(xiàn)[6]提出基于無限脈沖響應(yīng)的全通濾波器優(yōu)化方法,先將其簡化為線性相位優(yōu)化,通過求解由Toeplitz-plus-Hankel矩陣構(gòu)成的線性方程組得到濾波器系數(shù),但這兩種方法都需要進(jìn)行矩陣求逆,尤其濾波器長度較長時(shí),計(jì)算量很大,引起很多問題,不適合實(shí)時(shí)應(yīng)用。
本文提出了一種新的子帶脈沖壓縮方法,首先設(shè)計(jì)頻帶分割濾波器組。原型濾波器的設(shè)計(jì),沒有采用窗函數(shù)的非線性優(yōu)化或者切比雪夫逼近法減小重構(gòu)誤差,也避免了求影響優(yōu)化方法性能和有效性的逆矩陣的傳統(tǒng)設(shè)計(jì)方法,而是將通帶誤差、阻帶殘余能量和失真轉(zhuǎn)移函數(shù)在正交頻率w=pi/2處的平方誤差的加權(quán)和定義為誤差函數(shù),通過無約束變尺度方法[7]使其最小化,得到原型濾波器的系數(shù)。最后對(duì)超寬帶雷達(dá)信號(hào)進(jìn)行了仿真,仿真結(jié)果驗(yàn)證了該算法的正確性和有效性。
1 子帶脈沖壓縮原理
設(shè)接收信號(hào)為x(n),脈沖壓縮后的輸出信號(hào)為 y(n),對(duì)應(yīng)的Z變換分別為X(Z),Y(Z)。
子帶脈沖壓縮的基本原理:將接收信號(hào)通過分析濾波器組分成子帶信號(hào),對(duì)每個(gè)子帶信號(hào)進(jìn)行抽取,匹配信號(hào)為每個(gè)子帶信號(hào)頻譜復(fù)共軛,接收信號(hào)頻譜與匹配信號(hào)頻譜相乘,得到子帶脈壓結(jié)果,對(duì)其進(jìn)行同等倍數(shù)的插值后通過綜合濾波器組,得到寬帶脈沖壓縮信號(hào)。圖1給出了子帶脈沖壓縮的結(jié)構(gòu)圖。H1(Z),H2(Z)分別是正交鏡像濾波器中分析濾波器的低通和高通濾波器,F(xiàn)1(Z),F(xiàn)2(Z)對(duì)應(yīng)的是綜合濾波器的低通和高通濾波器。
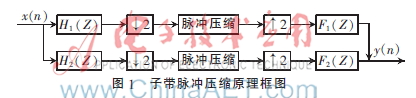
由抽取內(nèi)插理論以及正交鏡像濾波器組性質(zhì)可簡化得到:
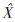 (Z)=1/2[H12(Z)-H12(-Z)]X(Z)(1)
(Z)=1/2[H12(Z)-H12(-Z)]X(Z)(1)
令
T(Z)=1/2[H12(Z)-H12(-Z)](2)
為獲得完全重建濾波器組,應(yīng)滿足以下條件:
T(Z)=1/2[H12(Z)-H12(-Z)]=cZ-n0(3)
由式(3)可知,若H1(Z)是一個(gè)線性相位濾波器,則T(Z)也是一個(gè)線性相位濾波器,可消除相位失真。由數(shù)字信號(hào)理論可知,當(dāng)N階FIR濾波器滿足奇對(duì)稱或偶對(duì)稱時(shí),F(xiàn)IR濾波器為嚴(yán)格線性相位,又H1(Z)為低通濾波器,則低通濾波器的脈沖響應(yīng)滿足:
h1(n)=h1(N-1-n),0≤n≤N-1(4)
式(4)中,N為濾波器長度。
對(duì)應(yīng)的頻率響應(yīng)為:
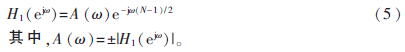
將式(5)代入到式(3)可得:
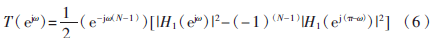
當(dāng)N為奇數(shù)、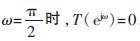 。在正交頻率點(diǎn)處會(huì)導(dǎo)致嚴(yán)重的幅度失真,因此,N必須為偶數(shù)。對(duì)所有
。在正交頻率點(diǎn)處會(huì)導(dǎo)致嚴(yán)重的幅度失真,因此,N必須為偶數(shù)。對(duì)所有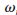 ,完全重建條件可寫為:
,完全重建條件可寫為:
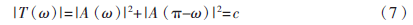
消除混疊失真和相位失真后,由于濾波器的鏡像對(duì)稱約束條件,只能減小幅度失真,不能完全消除。
2 QMF的FIR原型濾波器設(shè)計(jì)
不難看出,正交鏡像濾波器組的設(shè)計(jì)關(guān)鍵在于低通原型濾波器H1(Z)的設(shè)計(jì)。定義誤差函數(shù)為:

其中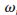 p和
p和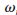 s分別為通帶和阻帶的邊界頻率。對(duì)于長度為偶數(shù)的實(shí)對(duì)稱序列h1(n),對(duì)應(yīng)的幅頻響應(yīng)H1(ej
s分別為通帶和阻帶的邊界頻率。對(duì)于長度為偶數(shù)的實(shí)對(duì)稱序列h1(n),對(duì)應(yīng)的幅頻響應(yīng)H1(ej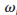 )為:
)為:

其中W,Z是實(shí)對(duì)稱正定矩陣。
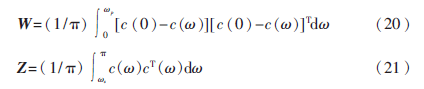
則目標(biāo)函數(shù)E可表示為:
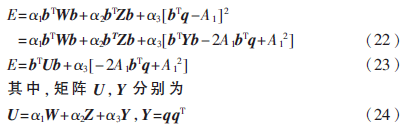
式(22)給出了目標(biāo)函數(shù)的表達(dá)式,是一個(gè)二次函數(shù),矩陣U為對(duì)稱正定矩陣,因此,可通過無約束的變尺度方法對(duì)誤差函數(shù)E進(jìn)行最小化,得到最優(yōu)系數(shù)。
設(shè)迭代第i步的最小值為bi,搜索方向的最優(yōu)步長是λi,則bi+1可用下式(25)計(jì)算:

3 仿真分析
參數(shù)設(shè)置:取濾波器長度N=24,通帶頻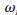 p=0.4π,
p=0.4π,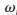 s=0.6π,
s=0.6π, 1=0.7,
1=0.7, 2=0.1,
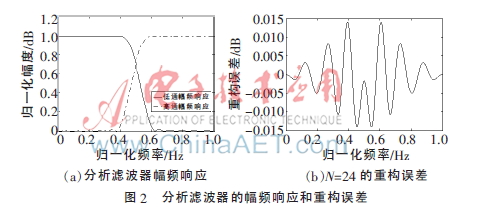
2=0.1, 3=1。圖2(a)給出了分析濾波器低通和高通的歸一化幅頻響應(yīng)。圖2(b)為正交鏡像濾波器組的重建誤差。該算法的主要性能參數(shù):峰值重建誤差PRE=0.013 9,通帶誤差Ep=1.162×10-8,阻帶誤差Es=7.48×10-5,阻帶邊緣衰減As=25.06 dB。
3=1。圖2(a)給出了分析濾波器低通和高通的歸一化幅頻響應(yīng)。圖2(b)為正交鏡像濾波器組的重建誤差。該算法的主要性能參數(shù):峰值重建誤差PRE=0.013 9,通帶誤差Ep=1.162×10-8,阻帶誤差Es=7.48×10-5,阻帶邊緣衰減As=25.06 dB。
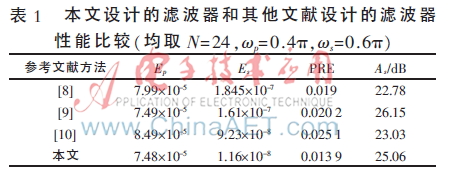
表1給出了本文設(shè)計(jì)的濾波器和其他文獻(xiàn)設(shè)計(jì)的濾波器性能比較。
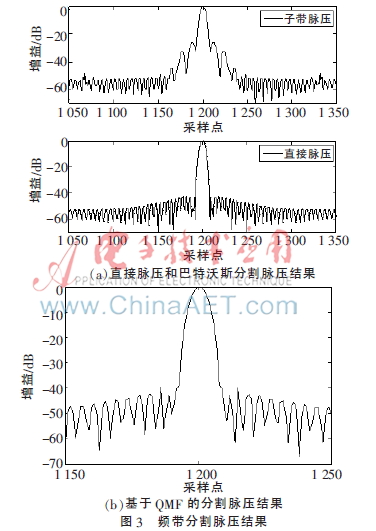
線性調(diào)頻信號(hào)參數(shù)設(shè)置:脈沖寬度T=2 s,帶寬B=150 MHz,采樣頻率F=300 MHz。圖3給出了不同方法的頻帶分割加海明窗后的最終脈壓結(jié)果。直接脈壓主副瓣比約為42 dB,利用巴特沃斯分割主副瓣比僅28.62 dB,而采用本文的正交鏡像濾波器設(shè)計(jì)方法,可將主副瓣比提高到約40 dB,主瓣寬度幾乎相同。最大子帶脈壓誤差由原來的32 dB降低到23 dB。
4 結(jié)束語
本文提出了一種新的子帶脈沖壓縮方法。本方法主要?jiǎng)?chuàng)新點(diǎn)在于:一是正交鏡像濾波器的設(shè)計(jì),拋棄了傳統(tǒng)的窗函數(shù)或等波紋逼近法設(shè)計(jì)原型濾波器方法,而是采用變尺度方法,通過優(yōu)化原型濾波器系數(shù)使誤差函數(shù)達(dá)到最小,設(shè)計(jì)的濾波器與其他幾種文獻(xiàn)設(shè)計(jì)的方法相比,其峰值重建誤差、通帶和阻帶誤差均有所減小。二是采用了將正交鏡像濾波器作為頻帶分割濾波器的子帶脈沖壓縮方法,該方法的優(yōu)越性主要表現(xiàn)在:與現(xiàn)有的通過頻譜搬移實(shí)現(xiàn)多通道綜合的脈沖壓縮方法相比,消除了相鄰?fù)ǖ乐g的混疊失真和相位失真,幅度失真也降到最小,使子帶脈壓后的結(jié)果和直接脈壓結(jié)果更為接近,仿真結(jié)果驗(yàn)證了該算法的有效性。
參考文獻(xiàn)
[1] 李志強(qiáng),劉利民,馬彥恒.雷達(dá)信號(hào)的高速數(shù)據(jù)采集處理系統(tǒng)的設(shè)計(jì)[J].電子技術(shù)應(yīng)用,1998,24(12):34-35.
[2] 水鵬朗,保錚.基于頻帶分割的超寬帶雷達(dá)脈沖壓縮方法[J].電子學(xué)報(bào),1999,27(6):50-53.
[3] CHEN D, QU D, JIANG T, et al. Prototype filter optimization to minimize stopband energy with NPR constraint for filter bank multicarrier modulation systems[J]. IEEE Trans. on Signal Processing, 2013,61(1):159-169.
[4] SHARMA K K, JOSHI S D,SHARMA S. Advances in Shannon sampling theory[J]. Defence Science Journal, 2013,63(1):41-45.
[5] CHEN C K, LEE J H. Design of quadrature mirror filters with linear phase in the frequency domain[J]. IEEE Trans. Circuits Syst, 1992, 39(9):593-605.
[6] STANCIC G, NIKOLIC S. Digital linear phase notch filter design based on IIR all-pass filter application[J]. Digital Signal Processing, 2013,23(3):1065-1069.
[7] RAO S S. Engineering optimization theory and practice[M].New Delhi: New Age International (P) Limited, 1998.
[8] UPENDAR J, GUPTA C P,SINGH G K. Designing of two channel quadrature mirror filter bank using Particle Swarm Optimization[J]. Digital Signal Processing, 2010,20(10):304-313.
[9] KUMAR A, SINGH G K, ANAND R S. An improved method for the designing quadrature mirror filter banks via unconstrained optimization[J]. J. Math. Model. Algorithm, 2010,9(1):99-111.
[10] OM P S, SONI M K, TALWAR I M. Marquardt optimization method to design two channel quadrature mirror filter banks[J]. Digital Signal Process,2006,16(6):870-879.

