摘 要: 根據(jù)理想導(dǎo)體的邊界條件建立線、面連接結(jié)構(gòu)的電場(chǎng)積分方程。該積分方程運(yùn)用矩量法直接進(jìn)行計(jì)算時(shí),隨著電尺寸增大,計(jì)算量和存儲(chǔ)量就會(huì)迅速增加,進(jìn)而降低了求解的效率。為了降低計(jì)算量和存儲(chǔ)量,運(yùn)用H2矩陣方法的可容許條件將阻抗矩陣元素劃分為遠(yuǎn)區(qū)場(chǎng)的矩陣塊和近區(qū)場(chǎng)的矩陣塊。近區(qū)場(chǎng)的矩陣塊直接用矩量法計(jì)算并進(jìn)行存儲(chǔ),遠(yuǎn)區(qū)場(chǎng)的矩陣塊通過(guò)H2矩陣的層間插值的方法進(jìn)行處理并存儲(chǔ),從而有效地降低了計(jì)算量和存儲(chǔ)量。
關(guān)鍵詞: MoM;H2矩陣;電場(chǎng)積分方程
0 引言
實(shí)際工程問題中,常常遇到線天線與平臺(tái)相連的情況(例如飛機(jī)、輪船、手機(jī)上的天線等),于是求解這類的電場(chǎng)積分方程問題具有非常重要的意義。
可是運(yùn)用矩量法(MoM)[1]直接求解計(jì)算該積分方程時(shí),隨著目標(biāo)電尺寸增大,計(jì)算量和存儲(chǔ)量就會(huì)迅速增加,進(jìn)而降低了求解的效率。隨著電磁數(shù)值計(jì)算的發(fā)展,陸續(xù)地提出了不少快速算法,例如FMM[2]、MLFMA[3]、CG-FFT以及H-Matrix[4-5]等,雖然這些算法中最好的已經(jīng)能夠?qū)⒂?jì)算量和存儲(chǔ)量從最初的O(N2)和O(N3)的數(shù)量級(jí)降低到O(NlogN)的數(shù)量級(jí),但是這并不是最理想的情況,當(dāng)未知量N繼續(xù)增大時(shí),O(NlogN)的數(shù)量級(jí)還是很驚人的。于是本文通過(guò)結(jié)合H2-Matrix[6]算法實(shí)現(xiàn)將數(shù)量級(jí)降低到O(N)線性階的關(guān)系。
1 線面連接結(jié)構(gòu)的積分方程的構(gòu)建
空間中任意一點(diǎn)的散射電場(chǎng)Es(r)是由線面連接結(jié)構(gòu)的面電流密度Js(r)和線電流密度Jw(r)二者綜合作用產(chǎn)生的,表達(dá)式為:
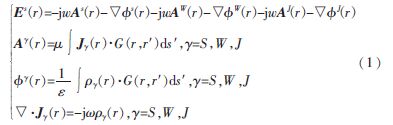
其中,A(r)表示磁矢量位;S,W,J,分別表示面、線、連接點(diǎn)三種情況;G(r,r′)表示三維格林函數(shù);k是自由空間波數(shù);ρ(r)表示感應(yīng)電荷密度;r,r′分別表示場(chǎng)點(diǎn)和源點(diǎn)。
理想導(dǎo)體表面的切向電場(chǎng)邊界條件為:

其中,為單位切向矢量。
將式(1)代入式(2)得到:

2 H 2矩陣求解積分方程
式(3)中的未知量Jγ(r)可以用一組線性不相關(guān)的基函數(shù)fnγ(r)展開,理想導(dǎo)體的表面部分選用RWG基函數(shù)[7],導(dǎo)線部分選用三角基函數(shù),而線-面連接點(diǎn)選用連接基函數(shù)[8],然后運(yùn)用伽略金法得到矩陣形式ZI=V的積分方程如下:
ZSS ZSW ZSJZWS ZWW ZWJZJS ZJS ZJJ·ISIWIJ=ESEWEJ(4)
對(duì)于式(4)中的阻抗矩陣Z中的元素運(yùn)用可容性條件[5]將其劃分為近區(qū)塊和遠(yuǎn)區(qū)塊。
近區(qū)塊中的阻抗矩陣元素是不可容的,直接采用矩量法進(jìn)行計(jì)算。
而對(duì)于遠(yuǎn)區(qū)塊中可容的阻抗矩陣元素運(yùn)用H2矩陣方法計(jì)算。遠(yuǎn)區(qū)塊的核函數(shù)-格林函數(shù)采用Lagrange多項(xiàng)式[9]進(jìn)行退化核處理。于是式(3)中的核函數(shù)G(r,r′)可以寫成如下形式:

其中,相應(yīng)的Lagrange多項(xiàng)式,Kt和Ks為相應(yīng)的插值點(diǎn)個(gè)數(shù)。將式(5)帶入阻抗元素表達(dá)式可得


這就意味著只需要存儲(chǔ)葉子簇E矩陣Vt并且使用轉(zhuǎn)移矩陣E就可以精確地表示所有的簇樹,因?yàn)檗D(zhuǎn)移矩陣只需要k(t′)k(t)個(gè)存儲(chǔ)單元,而矩陣Vt需要tgk(t)個(gè)存儲(chǔ)單元,k(t)=t,因此H2矩陣的嵌套結(jié)構(gòu)有效節(jié)省了存儲(chǔ)量。從而使H2矩陣的計(jì)算量和存儲(chǔ)量近似達(dá)到線性階O(N)。
下面就運(yùn)用存儲(chǔ)量小、步收斂性、穩(wěn)定性高的共軛梯度迭代法[10-12]求解矩陣-向量方程,得出感應(yīng)電流。
3 數(shù)值算例

算例1 為了驗(yàn)證矩量法結(jié)合H2矩陣方法的正確性,首先計(jì)算了頻率為300 MHz的均勻平面波,它沿θ=0°,φ=0°入射到半徑為0.8λ的金屬球上,其中散射方向?yàn)棣?0°~180°,φ=0°。通過(guò)對(duì)兩種計(jì)算方法結(jié)果的比較(如圖1所示)可以判斷出H2矩陣方法的正確性。

算例2 電磁波頻率f=300 MHz,輻射方向?yàn)棣?0°~180°,激勵(lì)采用連接點(diǎn)饋電,分別計(jì)算了0.6λ~ 2.8λ,H2矩陣算法與MoM分別計(jì)算時(shí)存儲(chǔ)量隨未知量的變化,以及阻抗矩陣元素計(jì)算時(shí)間量隨未知量的變化,結(jié)果如圖2和圖3所示。從圖2、圖3可以看出,H2矩陣算法不管是阻抗矩陣元素的求解時(shí)間還是總的程序求解時(shí)間都明顯比MoM要少,并且可以看出H2矩陣算法的計(jì)算量隨未知量的變化近似呈線性階O(N)的增長(zhǎng)趨勢(shì)。

圖4給出了H2矩陣算法與矩量法求解電場(chǎng)積方程所需存儲(chǔ)量隨未知量變化的曲線圖。由圖4可知,MoM計(jì)算時(shí)所需的存儲(chǔ)量隨著未知量的變化呈O(N2)的關(guān)系迅速增加,而H2矩陣所需的存儲(chǔ)量與未知量之間的關(guān)系呈線性階O(N)的變化趨勢(shì)。
4 結(jié)論
本文采用H2矩陣算法計(jì)算電場(chǎng)積分方程,通過(guò)傳遞矩陣的嵌套方法能夠有效地將計(jì)算所需的存儲(chǔ)量和計(jì)算量近似降低到線性階O(N)。同時(shí)H2矩陣算法對(duì)模型并沒有具體的要求,可以推廣到求解任意導(dǎo)體線面結(jié)構(gòu)的模型。
參考文獻(xiàn)
[1] GIBSON W C. The method of moments in electromagnetics[M]. CRC Press, 2007.
[2] CHENG H, GREENGARD L, ROKHLIN V. A fast adaptive multipole algorithm in three dimensions[J]. Journal of Computational Physics, 1999, 155(2): 468-498.
[3] ROKHLIN V. Rapid solution of integral equations of scattering theory in two dimensions[J]. Journal of Computational Physics, 1990, 86(2): 414-439.
[4] HACKBUSCH W. A sparse matrix arithmetic based on H-Matrices. Part I: introduction to H-Matrices[J]. Computing, 1999, 62(2):89-108.
[5] HACKBUSCH W, KHOROMSKIJ B N. A Sparse-matrix arithmetic[J]. Computing, 2000, 64(1): 21-47.
[6] B?魻RM S. H2-matrices-multilevel methods for the approximation of integral operators[J]. Computing and Visualization in Science, 2004,7(3-4):173-181.
[7] RAO S, WILTON D, GLISSON A. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation, 1982,30(3):409-418.
[8] HWU S U, WILTON D R, RAO S M. Electromagnetic scattering and radiation by arbitrary conducting wire/surface configurations[C]. IEEE Society International Symposium on Antennas and Propagation, Syracuse, NY, USA, 1988, 2:890-893.
[9] 唐松生,隋樹林.拉格朗日插值多項(xiàng)式[J].青島化工學(xué)院學(xué)報(bào),1992(4):101-105.
[10] 王學(xué)忠,黃廷祝,李良,等.H-矩陣方程組的預(yù)條件迭代法[J].計(jì)算數(shù)學(xué),2007,29(1):89-98.
[11] 鄭麗.幾種共軛梯度法的研究[D].重慶:重慶大學(xué),2009.
[12] 張穎.有關(guān)共軛梯度法的一些研究[D].大連:大連理工大學(xué),2012.

