摘 要: 擴散映射(Diffusion Maps)是一種基于流形學習的非線性降維方法。基于對擴散映射的研究,提出了一種新的非線性降維算法。根據(jù)近鄰點分布的不同和模糊聚類原理,新算法定義了擴散映射算法構(gòu)建權(quán)值矩陣的誤差近似系數(shù),并采用改進的距離公式來選取樣本點的近鄰點,很大程度地降低了近鄰點的選取對降維效果的影響。實驗結(jié)果表明,新算法有效地保持了高維數(shù)據(jù)中的流形結(jié)構(gòu),具有更好的降維效果,并在基于內(nèi)容的圖像檢索中達到很高的查準率,新算法的有效性和優(yōu)越性得到了證實。
關(guān)鍵詞: 擴散映射;降維;流形學習;聚類
0 引言
流形是局部具有歐幾里得空間性質(zhì)的空間,包括各種維數(shù)的曲線、曲面等,是一般的幾何對象的總稱。流形學習[1-3]以流形理論為基礎(chǔ),把高維空間中的樣本集在低維空間中重新表示出來,并能求出其相應的嵌入映射,很好地保持了樣本點的拓撲結(jié)構(gòu),達到了維數(shù)約簡的目的。流形學習方法減少了高維數(shù)據(jù)的冗余性,解決了維數(shù)災難的問題,因此,流形學習具有非常重要的研究意義。目前,流形學習的方法主要分為兩類:一類是線性降維方法,主要有主成分分析(Principal Component Analysis,PCA)[4]、獨立分量分析(Independent Component Analysis,ICA)[5]、多維尺度分析(Multidimensional Scaling,MDS)[6]等;另一類是非線性降維方法,主要有核主成分分析(Kernel Principal Component Analysis,KPCA)[7]、等度規(guī)映射(Isometric Mapping,Isomap)[8]、局部線性嵌入(Locally Linear Embedding,LLE)[9]等。
擴散映射(Diffusion Maps,DM)[10]是COIFMAN R等人在2006年提出的一種基于流形學習的非線性降維方法,其主要思想來自于動力系統(tǒng)。作為一種新的流形學習框架,擴散映射通過在擴散過程中盡可能地保持擴散距離來進行降維,即保持樣本點的局部結(jié)構(gòu)不變,通過局部關(guān)系定義全局關(guān)系,使樣本點在低維空間中仍保持這種穩(wěn)定的全局關(guān)系。近鄰點選取和分布的不同可產(chǎn)生不同的鄰接圖,對擴散映射的降維效果影響很大,由此本文提出了一種改進的算法。由于聚類的中心含有大量的信息,新算法根據(jù)聚類原理,先定義了擴散映射構(gòu)建權(quán)值矩陣的誤差近似系數(shù),然后利用改進的距離函數(shù)來選取近鄰點,構(gòu)建鄰接圖。新算法模糊了近鄰點的選取對實驗結(jié)果的影響,達到了較為理想的降維效果,并在實驗中得到了證實。
1 Diffusion Maps(DM)算法
DM算法主要分為如下4步:
(1)構(gòu)建鄰接圖。對于給定的數(shù)據(jù)集X={x1,x2,…,xN},xi∈RD,i=1,2,…,N,若xi是xj的近鄰點,則將xi與xj之間賦一個邊,邊反映了樣本點之間的局部關(guān)系,近鄰點一般用歐氏距離來度量,距離公式為: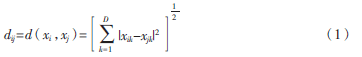
(2)構(gòu)建權(quán)值矩陣W。權(quán)值矩陣的元素Wij(W(xi,xj))反映樣本點xi與xj之間的相似程度,因此滿足:
①W是對稱的:Wij=Wji;
②W是非負的:Wij≥0。
一般采用高斯核函數(shù)定義成對數(shù)據(jù)點之間的相似度矩陣,即:
其中,![4EN0F92~XUQE`@NW)]@@MA6.png 4EN0F92~XUQE`@NW)]@@MA6.png](http://files.chinaaet.com/images/2016/01/29/6358967968187900009366336.png) 為高斯核的方差,
為高斯核的方差,![4EN0F92~XUQE`@NW)]@@MA6.png 4EN0F92~XUQE`@NW)]@@MA6.png](http://files.chinaaet.com/images/2016/01/29/6358967966271000008450640.png) 越大,權(quán)值越大,數(shù)據(jù)點間的相似程度越大。
越大,權(quán)值越大,數(shù)據(jù)點間的相似程度越大。
(3)構(gòu)建擴散核矩陣K。利用加權(quán)的圖Laplacian歸一化方法。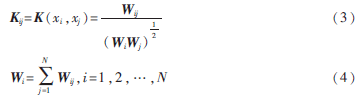
其中,Wi表示xi與其他各點的權(quán)值之和。
(4)核矩陣K的特征分解。對內(nèi)積矩陣K進行特征分解,求K的特征值和特征向量,K的最大的d個特征值λ1,λ2,…,λd對應的特征向量為U=[u1,u2,…,ud],則高維數(shù)據(jù)X降維后的數(shù)據(jù)集為Y=UT=[u1,u2,…,ud]T。
2 新算法的提出
2.1聚類原理
聚類是解決高維數(shù)據(jù)問題的常用方法。聚類分類產(chǎn)生一些簇,簇是一組數(shù)據(jù)對象的集合,同一簇中的對象相似,不同簇中的對象相異,每個簇的中心含有豐富的可利用的信息,具有代表性。模糊C均值(Fuzzy C-Means,F(xiàn)CM)算法[11-13]是應用最廣泛的聚類分析方法之一。
對于給定的采樣于維流形的高維觀測數(shù)據(jù)集X={x1,x2,…,xN},xi∈RD,i=1,2,…,D。設(shè)樣本點聚類分類的類別個數(shù)為M,第j類樣本的中心為cj,第j類樣本的個數(shù)為rj,總體樣本的中心為c。則定義第j類樣本點的類內(nèi)平均距離為: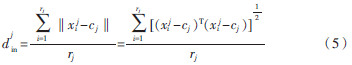
第j類樣本中心與總體樣本中心的距離為: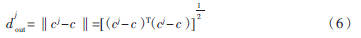
其中,‖‖表示歐式距離。由此,定義樣本點構(gòu)建權(quán)值矩陣的誤差近似系數(shù)為:
其中,j為樣本點xi所屬的類。
用誤差近似系數(shù)重新構(gòu)建樣本點在低維空間上嵌入的權(quán)值矩陣,從而提高樣本點之間的相似程度,獲得更好的實驗結(jié)果。
2.2 改進的距離函數(shù)
對于分布不均勻的數(shù)據(jù)集,假設(shè)P為分布密集的區(qū)域上的點,其k個近鄰點所占的區(qū)域為SP,O為分布稀疏的區(qū)域上的點,其k個近鄰點所占的區(qū)域為SO,顯然SP要比SO小得多。因此對于分布不均勻的樣本集,近鄰點k個數(shù)的選取會影響實驗結(jié)果。所以要對近鄰點間的距離進行改進,降低樣本點分布的影響。下面定義一種新的距離[14-15]。

其中,Gi、Gj分別表示xi、xj和其他點之間距離的平均值。
因為新的距離的分子是歐氏距離,分母是數(shù)值,則有:
①非負性:dij≥0,當且僅當xi=xj,即i=j時等號成立;
②對稱性:dij=dji;
③三角不等式性:dis+dsj≥dij。
由泛函分析知識可知,新的距離滿足距離空間的定義。在DM的第一步構(gòu)建鄰接圖時,采用新的距離公式取代歐氏距離來選取樣本點的k個近鄰點。新的距離使分布較密集區(qū)域的樣本點間的距離增大,而使分布較稀疏區(qū)域的樣本點間的距離縮小,這樣區(qū)域SP和SO區(qū)域的差異性減小,樣本點的整體分布趨于均勻化,從而降低樣本點的分布對算法效果的影響。
2.3改進的算法(Improved Diffusion Maps,IMDM)
IMDM算法的步驟如下:
(1)對樣本集進行聚類分類,得出構(gòu)建權(quán)值矩陣的誤差近似系數(shù):
(2)構(gòu)建鄰接圖。距離公式為: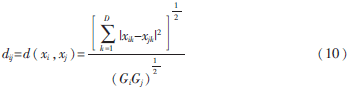
(3)構(gòu)建權(quán)值矩陣W′。
(4)構(gòu)建擴散核矩陣K′。
(5)核矩陣K′的特征分解。求K′的特征值和特征向量,K′的最大的d個特征值λ′1,λ′2,…,λ′d對應的特征向量為U′=[u′1,u′2,…,u′d],則高維數(shù)據(jù)X降維后的數(shù)據(jù)集為Y=[U′]T=[u′1,u′2,…,u′d]T。
新算法首先對樣本集進行聚類分類,利用類別信息得出構(gòu)建權(quán)值矩陣的誤差近似系數(shù),然后采用新的距離函數(shù)選取近鄰點構(gòu)建鄰接圖,這樣可適當降低近鄰點個數(shù)k的選取對算法的影響,得到較好的降維效果。
3 實驗結(jié)果及分析
3.1人工數(shù)據(jù)
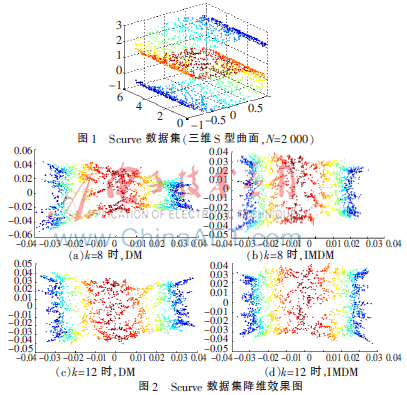
用DM和IMDM對Scurve人工數(shù)據(jù)集(如圖1所示)進行降維,實驗選取2 000個樣本點,近鄰點的個數(shù)分別取8、12,將數(shù)據(jù)集降至2維,實驗結(jié)果如圖2所示。從圖2中可以看出,IMDM比DM具有更好的降維效果,模糊了近鄰點個數(shù)的選取,降維效果比較理想,具有更好的可視化效果。
3.2 圖像檢索
在基于內(nèi)容的圖像檢索實驗中,圖像選自Corel數(shù)據(jù)庫,共1 000幅圖像,類別為10種,有建筑、風景、人物、動物、植物等。實驗對第450號恐龍圖像進行相關(guān)圖像檢索,降至維數(shù)d分別取6、14、20,檢索出的圖像數(shù)目設(shè)為20。實驗一先用DM方法對圖像數(shù)據(jù)集降維然后進行檢索,得出實驗結(jié)果如圖3中的(a)、(c)、(e)所示。實驗二先用IMDM方法對圖像數(shù)據(jù)集降維再進行檢索,得出實驗結(jié)果如圖3中的(b)、(d)、(f)所示。對比兩次實驗結(jié)果,可以清晰地看出,IMDM降維后進行基于內(nèi)容的圖像檢索的準確率明顯高于DM的。

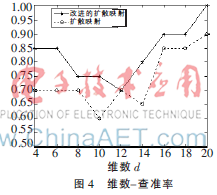
查準率是衡量圖像檢索算法有效性的常用指標,查準率越高,表示圖像檢索方法越好,反之越差。
圖4為在維數(shù)不同時,DM和IMDM查準率的變化情況。可以看出,多數(shù)情況下IMDM降維后圖像檢索的查準率高于DM的。特別地,當維數(shù)為20時,應用IMDM方法,查準率達到了100%。
4 結(jié)論
本文對基于流形學習的擴散映射非線性降維方法進行了分析研究,提出了一種改進的擴散映射非線性降維方法。此方法以聚類分類原理構(gòu)造權(quán)值矩陣的誤差近似系數(shù),通過改變樣本點間的距離公式重新構(gòu)建鄰接圖,進而實現(xiàn)降維。新算法有效地降低了近鄰點的選取對降維效果的影響,并且很好地保留了原始數(shù)據(jù)的拓撲結(jié)構(gòu)。將改進的擴散映射方法用于Scurve數(shù)據(jù)集和基于內(nèi)容的圖像檢索實驗,都得到了很好的效果,具有很好的實際應用價值。
參考文獻
[1] ORSENIGO C, VERCELLISN C. Kernel ridge regres-sion for out-of-sample mapping in supervised manifold learning[J]. Expert Systems with Application, 2012,39(9):7757-7762.
[2] 曹林林.基于流形學習的分類技術(shù)[D].濟南:山東師范大學,2013.
[3] 王自強,錢旭,孔敏.流形學習算法綜述[J].計算機工程與應用,2008,44(35):9-12.
[4] 曾憲華,羅四維.全局保持的流形學習算法對比研究[J].計算機工程與應用,2010,46(15):1-6.
[5] HYVARINEN A, OJA E. Independent component analysis:algorithms and applications[J]. Neural Networks, 2000,13(45): 411-430.
[6] COX T, COX M. Multidimensional scaling[M]. London:Chapman&Hall, 1994.
[7] SCHOLKOPF B, SMOLA A, MULLER K R. Nonliner co- mponent analysis as a kernel eigenvalue problem[J]. Neural Computation,1998,10(5):1299-1319
[8] THEODORIDIS S,KOUTROUMBAS K.模式識別(第4版)[M].李晶皎,王愛俠,王驕,等譯.北京:電子工業(yè)出版社,2010.
[9] Zhang Zhenyue, Zha Hongyuan. Principal manifold and nonlinear dimensionality reduction via local tangent space alignment[J]. SIAM Journal of Scientific Computing, 2004,26(1):313-338.
[10] COIFMAN R, LAFON S. Diffusion maps. Applied and computational harmonic analysis[EB/OL]. [2006-05-30].http: www.elsevier.com/locate/acha.
[11] 姜倫,丁華福.關(guān)于模糊C-均值(FCM)聚類算法的改進[J].計算機與數(shù)字工程,2010,38(2):4-6.
[12] 蘇錦旗,張文宇.基于模糊聚類的改進LLE算法[J],計算機與現(xiàn)代化,2014,225(5):9-13.
[13] BEZDEK J C, EHRLICH R. Full W. FCM: the fuzzy c-means clustering algorithm[J]. Computers & Geosciences,1984,10(2):191-203.
[14] 王和勇,鄭杰,姚正安.基于聚類和改進距離的LLE方法在數(shù)據(jù)降維中的應用[J],計算機研究與發(fā)展,2006,43(8):1485-1490.
[15] JOSHUA B T, VIN.DE S, LANGFORD J C. A global geometric framework for nonliner dimensionality reduction[J]. Science, 2000,290:2319-2323.

