摘  要： 為了標(biāo)定基于線結(jié)構(gòu)光的三維測量系統(tǒng)中的旋轉(zhuǎn)軸,，提出了一種基于圓錐體參照物的快速標(biāo)定方法。將一個(gè)圓錐體的參照物固定放置在旋轉(zhuǎn)平臺(tái)上,，控制旋轉(zhuǎn)臺(tái)每隔一定角度旋轉(zhuǎn)一次,，分別采集每個(gè)位置的圖像，對圖像預(yù)處理后,，提取圓錐體的亞像素邊緣,，通過擬合圓錐體邊緣直線，計(jì)算得到兩條邊緣直線的空間直線方程,，并利用Levenberg-Marquardt迭代法計(jì)算出空間中距離兩條邊緣直線最近的點(diǎn)作為圓錐體的頂點(diǎn),，然后根據(jù)得到的所有頂點(diǎn)擬合出所在的空間平面及空間圓的圓心，根據(jù)平面的法向量和圓心點(diǎn)建立起旋轉(zhuǎn)軸的直線方程,，完成旋轉(zhuǎn)臺(tái)的轉(zhuǎn)軸標(biāo)定,。實(shí)驗(yàn)結(jié)果表明，該標(biāo)定方法具有較高的標(biāo)定精度,。

　　關(guān)鍵詞： 圓錐體,；線結(jié)構(gòu)光；旋轉(zhuǎn)臺(tái),；標(biāo)定

0 引言

　　在光學(xué)三維測量中,，物體表面的測量因其速度快,、易于自動(dòng)化、非接觸等優(yōu)點(diǎn),，在工業(yè)檢測,、考古、生物醫(yī)學(xué),、逆向工程等領(lǐng)域具有非常重要的意義和廣闊的應(yīng)用前景,，因此得到越來越多相關(guān)領(lǐng)域的廣泛關(guān)注。在被動(dòng)式測量中,，由于線結(jié)構(gòu)光一次只能得到一條光條,，因此為了得到完整的物體表面三維信息還需要進(jìn)行一維掃描。一般有旋轉(zhuǎn)和平移兩種一維掃描方式,，若采用旋轉(zhuǎn)式掃描,，當(dāng)旋轉(zhuǎn)臺(tái)旋轉(zhuǎn)一周之后便可以得到物體整個(gè)表面的三維信息。

　　目前提出的基于線結(jié)構(gòu)光的旋轉(zhuǎn)臺(tái)轉(zhuǎn)軸標(biāo)定方法主要有三種：（1）基于標(biāo)準(zhǔn)圓柱體標(biāo)定轉(zhuǎn)臺(tái)中心的方法[1],，但該方法沒有考慮到旋轉(zhuǎn)臺(tái)與水平面的傾斜角度問題,；（2）用標(biāo)準(zhǔn)標(biāo)定球?qū)D(zhuǎn)軸進(jìn)行標(biāo)定[2]；（3）使用棋盤格標(biāo)定板進(jìn)行標(biāo)定轉(zhuǎn)臺(tái)[3],，但該方法沒有考慮到當(dāng)雙目相機(jī)的有效視場較小時(shí),，標(biāo)定板的旋轉(zhuǎn)角度有限，導(dǎo)致擬合的空間平面誤差增大,。此外參考文獻(xiàn)[4]提出使用多個(gè)控制點(diǎn)結(jié)合最小二乘法標(biāo)定轉(zhuǎn)軸,，但是沒有給出一種有效的求解方法。本文提出一種采用圓錐體對轉(zhuǎn)軸標(biāo)定的方法,，在滿足精度要求的前提下,，采用加工相對方便且精度符合要求的圓錐體靶標(biāo)，方法新穎,，標(biāo)定過程簡單,，算法較易實(shí)現(xiàn)。

1 測量系統(tǒng)構(gòu)成

　　基于線結(jié)構(gòu)光的三維測量系統(tǒng)主要由線結(jié)構(gòu)光激光器,、2臺(tái)工業(yè)相機(jī),、電動(dòng)旋轉(zhuǎn)臺(tái)、圖像采集卡和計(jì)算機(jī)組成,，如圖1所示,。

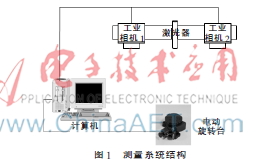
2 基本原理

　　如圖2所示，由于系統(tǒng)裝置安裝誤差,，導(dǎo)致了旋轉(zhuǎn)臺(tái)的轉(zhuǎn)軸方向與平行于世界坐標(biāo)系Yw的Y′軸方向之間有一定夾角,，從而導(dǎo)致測得的物體表面數(shù)據(jù)不可避免會(huì)有一定偏差。因此轉(zhuǎn)臺(tái)標(biāo)定是基于旋轉(zhuǎn)臺(tái)的線結(jié)構(gòu)光三維測量系統(tǒng)的重要一步,。

　　為了能夠精確地標(biāo)定旋轉(zhuǎn)臺(tái)轉(zhuǎn)軸參數(shù),，在旋轉(zhuǎn)臺(tái)旋轉(zhuǎn)角度已知的前提下,，利用Sobel算子和Zernike矩相結(jié)合的方法提取圓錐體的亞像素邊緣[5]。擬合兩條邊緣的兩條空間直線l1和l2的直線方程,，在空間中求取兩直線交點(diǎn)P（x,，y，z）,，把P點(diǎn)坐標(biāo)代入目標(biāo)函數(shù)：

　　利用Levenberg-Marquardt迭代法[6]求得使目標(biāo)函數(shù)達(dá)到最小的點(diǎn),，可以認(rèn)為P（x，y,，z）即為所有的圓錐頂點(diǎn)坐標(biāo)Pi（xi,，yi，zi）,。其中d為頂點(diǎn)P到直線l1和l2的距離,。最后根據(jù)最小二乘法擬合所有頂點(diǎn)所在的空間平面為：

　　Z=a0X+a1Y+a2（2）

　　由此可計(jì)算空間單位法向量為：

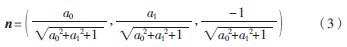
　　為了在平面上擬合平面圓計(jì)算圓心，可以把世界坐標(biāo)系下的轉(zhuǎn)軸方向向量n（nx,，ny,，nz）旋轉(zhuǎn)到轉(zhuǎn)臺(tái)坐標(biāo)系下，使其與世界坐標(biāo)系的Yw軸重合,，這樣在轉(zhuǎn)臺(tái)坐標(biāo)系下轉(zhuǎn)軸的方向向量就變?yōu)閘（0,，1，0）,，可采用羅德里格斯公式計(jì)算其繞法向量r（rx,，ry,，rz）旋轉(zhuǎn)的旋轉(zhuǎn)矩陣R[7],，具體公式為：

　　把所有頂點(diǎn)乘以旋轉(zhuǎn)矩陣R旋轉(zhuǎn)到轉(zhuǎn)臺(tái)坐標(biāo)系下后，頂點(diǎn)所在的平面與XOZ平面平行,，把這些點(diǎn)投影到XOZ平面后便可根據(jù)最小二乘法擬合XOZ平面上的頂點(diǎn)投影所在的平面圓進(jìn)而得到其圓心O′（x′0,，y′0，z′0）,，然后再把擬合得到的圓心O′逆向旋轉(zhuǎn)回世界坐標(biāo)系下后得到O0（x0,，y0，z0）,，即可得到旋轉(zhuǎn)軸的全部參數(shù),。

　　得到旋轉(zhuǎn)軸的參數(shù)后，計(jì)算出轉(zhuǎn)臺(tái)坐標(biāo)系與世界坐標(biāo)系的位置關(guān)系如圖3所示,。首先要計(jì)算N軸與Y′軸之間的夾角?漬,，然后將N軸投影到XOY平面，計(jì)算N軸的投影與X′軸之間的夾角,，之后便可以得到N軸繞Z′軸,、Y′軸旋轉(zhuǎn)到與XOZ平面平行的旋轉(zhuǎn)矩陣Ry,、Rz分別為：

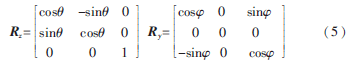
3 實(shí)驗(yàn)結(jié)果及分析

　　實(shí)驗(yàn)中采用鏡頭焦距為12 mm、分辨率為1 280×1 024的大恒DH-HV1310Fx型工業(yè)相機(jī),，線形激光器和大恒GCD-011080M電控旋轉(zhuǎn)臺(tái)搭建起了基于線結(jié)構(gòu)光的三維掃描系統(tǒng),。根據(jù)上述標(biāo)定原理，對該型號(hào)電動(dòng)旋轉(zhuǎn)臺(tái)進(jìn)行標(biāo)定實(shí)驗(yàn)和誤差分析,。

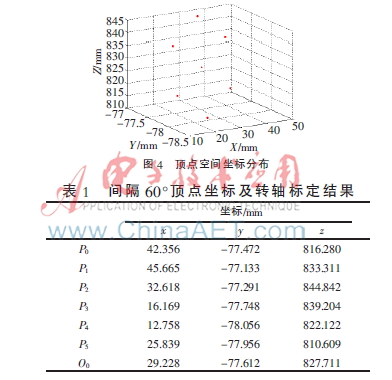
　　標(biāo)定使用圓錐體為工廠加工的直徑精度為9 m的圓錐工件,，將圓錐體固定放置在旋轉(zhuǎn)臺(tái)上，旋轉(zhuǎn)角度選擇每隔60°旋轉(zhuǎn)一次,，一共得到6個(gè)頂點(diǎn)坐標(biāo),。圖4所示分別為每隔60°圓錐體旋轉(zhuǎn)一周后頂點(diǎn)的三維坐標(biāo)分布。計(jì)算得到旋轉(zhuǎn)軸的方向向量n（nx,，ny,，nz）和圓心坐標(biāo)O0（x0，y0,，z0）的均值和標(biāo)準(zhǔn)差,。其中每隔60°旋轉(zhuǎn)得到的頂點(diǎn)的不同位置坐標(biāo)及計(jì)算得到的圓心坐標(biāo)如表1所示。

　　測量點(diǎn)Pi（xi,，yi,，zi）先通過轉(zhuǎn)軸標(biāo)定得到旋轉(zhuǎn)矩陣Rz和Ry旋轉(zhuǎn)到轉(zhuǎn)臺(tái)坐標(biāo)系下的坐標(biāo)為P″i（x″i，y″i,，z″i）,，然后繞旋轉(zhuǎn)軸N旋轉(zhuǎn)一定角度α后再通過逆向旋轉(zhuǎn)即可得到點(diǎn)P′i（x′i，y′i,，z′i）的坐標(biāo),，依次把每一組點(diǎn)云數(shù)據(jù)旋轉(zhuǎn)到不同方位即可得到被測物體的表面三維信息。轉(zhuǎn)臺(tái)坐標(biāo)之間的關(guān)系為：

　　其中,，（x0,，y0，z0）為轉(zhuǎn)軸上一點(diǎn)即轉(zhuǎn)臺(tái)中心O0,，α是每組點(diǎn)云之間轉(zhuǎn)臺(tái)旋轉(zhuǎn)的角度,，參見圖3。同理T-,、R-z,，R-x向相反的方向旋轉(zhuǎn)即可。

　　實(shí)驗(yàn)中根據(jù)標(biāo)定得到的參數(shù),，使用精密圓柱體標(biāo)準(zhǔn)件進(jìn)行掃描測量,，并對測量結(jié)果進(jìn)行了分析比較，圓柱體標(biāo)準(zhǔn)件的直徑為24.5±0.01 mm,，測量得到的圓柱體擬合直徑為24.541 5 mm,，測量結(jié)果與標(biāo)準(zhǔn)件的直徑精度相對一致,，距離擬合圓柱體表面最大正向誤差為0.118 3 mm，最大負(fù)向誤差為0.094 7 mm,，平均距離誤差為0.054 mm,。此外將一個(gè)茶杯放置在旋轉(zhuǎn)臺(tái)上，以 0.5°為旋轉(zhuǎn)間隔對其進(jìn)行掃描測量,，得到圖5所示濾除掉噪聲點(diǎn)的茶杯點(diǎn)云數(shù)據(jù)及三維重建后的茶杯模型,。

4 結(jié)論

　　本文提出的算法通過測量圓錐體參照物在旋轉(zhuǎn)臺(tái)不同位置的頂點(diǎn)，能夠較精確得到轉(zhuǎn)臺(tái)中心旋轉(zhuǎn)軸的參數(shù),，簡化了標(biāo)定過程,，標(biāo)定速度快，易操作,。實(shí)驗(yàn)結(jié)果表明,，該方法具有較高的標(biāo)定精度，具有一定的實(shí)用性,。其他基于旋轉(zhuǎn)臺(tái)的三維測量系統(tǒng)都可利用此標(biāo)定方法對旋轉(zhuǎn)軸進(jìn)行標(biāo)定,。

參考文獻(xiàn)

　　[1] 周會(huì)成，陳潔紅,，陽道善.一種新型三維視覺測頭的結(jié)構(gòu)與原理[J].電子測量與儀器學(xué)報(bào),，2000，14（2）：21-25.

　　[2] 徐永安,，楊欽,，懷進(jìn)鵬.激光旋轉(zhuǎn)掃描測量系統(tǒng)中轉(zhuǎn)軸標(biāo)定及多視拼合[J].中國激光，2005,，32（5）：659-662.

　　[3] 李懷澤,，沈會(huì)良，程岳.基于旋轉(zhuǎn)多視角深度配準(zhǔn)的三維重建方法[J].計(jì)算機(jī)應(yīng)用,，2012,，32（12）：3365-3368.

　　[4] 尹茂東.基于旋轉(zhuǎn)平臺(tái)的物體表面三維重建研究[D].青島：青島大學(xué),，2007.

　　[5] 姜邁,，梁曄，梁煒,，等.Zernike亞像素圖像矩邊緣檢測算子模型研究[J].計(jì)算機(jī)測量與控制,，2013，21（4）：874-876.

　　[6] LEVENBERG K. A method for the solution of certain nonlinear problems in least squares[J]. Quarterly Applied Mathematics,， 1944,，2：164-166.

　　[7] BRADKSI G， KAEBLE A. Learning OpenCV： computer vision with the OpenCV library[M]. Sebastopol,， California,， USA：O′Reilly Media Inc.,， 2008.