0 引言

    近年來,，四旋翼無人機(jī)因其結(jié)構(gòu)簡單,、操控靈活、可垂直起降及懸停等特性而被廣泛應(yīng)用于軍事,、民用等領(lǐng)域^[1],，飛行控制中對其姿態(tài)的精確控制最為關(guān)鍵,，但由于其易受陣風(fēng)干擾，建模的不精確性等諸多因素的影響,，如何設(shè)計出能精確跟蹤姿態(tài)角和姿態(tài)角速度的控制器逐漸引起了高?？蒲姓吆推髽I(yè)的廣泛重視。

    目前常用的控制方法有：PID算法^[2,，3]、反步法^[4],、線性二次調(diào)節(jié)(LQR)方法^[5],、積分滑模控制^[6]等,。本文利用雙環(huán)滑模方法對姿態(tài)角和角速度進(jìn)行跟蹤控制,，對于內(nèi)環(huán)模分析考慮了參數(shù)不確定和外界擾動的影響，外環(huán)模跟蹤虛擬控制量,，同時文中對所設(shè)計的控制器進(jìn)行了MATLAB/Simulink仿真驗證,，并與經(jīng)典PID算法和反步法跟蹤效果進(jìn)行了對比，結(jié)果表明在參數(shù)不確定及外界干擾條件下,，該控制器具有更好的跟蹤性和魯棒性,。

1 四旋翼飛行器建模

1.1 坐標(biāo)系建立

    由于四旋翼飛行器是一個復(fù)雜的多變量、非線性動態(tài)系統(tǒng),，對其建模必須做出合理的假定,，本文建模中假定^[7]：(1)飛行器結(jié)構(gòu)為剛體且均勻?qū)ΨQ；(2)螺旋槳對稱安裝于剛性十字架四端,，且在同一水平高度,；(3)質(zhì)心與機(jī)體坐標(biāo)系原點一致。

    首先是兩種坐標(biāo)系的建立,，即慣性坐標(biāo)系W和機(jī)體坐標(biāo)系B,，如圖1所示，ox_W y_W z_W為慣性坐標(biāo)系,，其中 z_W朝上,；ox_B y_B z_B為機(jī)體坐標(biāo)系，o為機(jī)體的重心,， z_B為垂直機(jī)體,，且當(dāng)四旋翼處于懸停狀態(tài)時方向朝上，x_B指向1號旋翼方向,，y_B指向2號旋翼方向,，3、4號旋翼分別在-x_B,、-y_B方向,。為確定兩坐標(biāo)系間的聯(lián)系,，使用Z-X-Y歐拉角定義飛行器繞 z_W軸轉(zhuǎn)動的角度為偏航角Ψ，繞x_B,、y_B軸轉(zhuǎn)動的角度分別為橫滾角φ和俯仰角θ,。則從 B系變換到 W系的旋轉(zhuǎn)矩陣為：

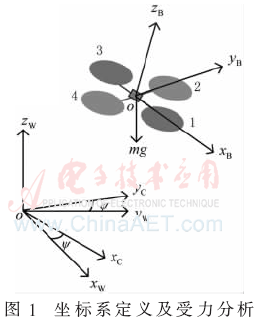
1.2 動力學(xué)模型建立

    將四旋翼看成六自由度剛體運(yùn)動，由四個電機(jī)帶動四個旋翼轉(zhuǎn)動提供動力,，實現(xiàn)空中姿態(tài)和豎直位移的變化,。每個旋翼產(chǎn)生一個升力F_i和垂直于飛行器螺旋槳的力矩M_i，根據(jù)牛頓第二定律和剛體運(yùn)動的歐拉方程,，飛行器的運(yùn)動方程包括動力學(xué)方程及通過坐標(biāo)變換關(guān)系得到的運(yùn)動學(xué)方程^[8],，如式(3)所示。 

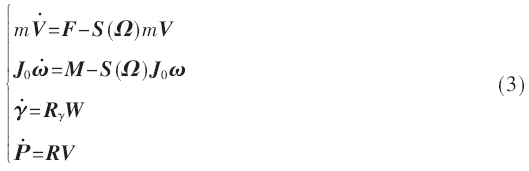
    存在參數(shù)不確定項和外部干擾力矩時的姿態(tài)角速度動力學(xué)方程則為：

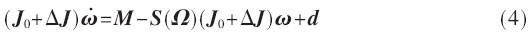
其中,，V=(u,，v，w)^T,、ω=(p,，q，r)^T分別為飛行器質(zhì)心相對機(jī)體坐標(biāo)系的三軸線速度和角速度,；P=(x,，y，z)^T表示相對慣性坐標(biāo)系的地面空間位置,；γ=(φ,，θ， Ψ)^T表示機(jī)體相對于地面坐標(biāo)系的姿態(tài)角,，分別表示機(jī)體坐標(biāo)系下所受外合力及各個姿態(tài)角力矩,；m為飛行器總質(zhì)量；J₀為飛行器繞質(zhì)心旋轉(zhuǎn)的轉(zhuǎn)動慣量矩陣,，ΔJ為該慣量陣的不確定項,；Ω表示斜對稱矩陣，對任意向量v∈R³,，有S(Ω)v=Ω×v,。d=(d_x，d_y,，d_z)^T為所受的外部干擾力矩,。

2 控制律設(shè)計

    雙環(huán)滑模控制的整體思想^[9]是設(shè)計合適的切換函數(shù)來實現(xiàn)積分滑模,。由于四旋翼姿態(tài)角速度變化明顯快于姿態(tài)角變化,，所以設(shè)計成內(nèi)外環(huán)結(jié)構(gòu)。設(shè)計控制系統(tǒng)如圖2所示,，對于內(nèi)環(huán)不僅考慮有噪聲干擾d,，而且引入了轉(zhuǎn)動慣量參數(shù)的攝動ΔJ,，只有確定合適的控制輸入量M，才能使四旋翼飛行器實際的姿態(tài)角與期望姿態(tài)角γ_d的誤差達(dá)到最小且響應(yīng)速度較快,。

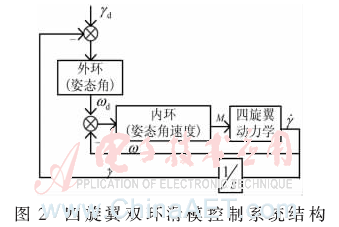
    該控制系統(tǒng)由外環(huán)（姿態(tài)角）和內(nèi)環(huán)（姿態(tài)角速度）兩個環(huán)路構(gòu)成,。角度?酌的跟蹤由外環(huán)實現(xiàn)，角速度γ的跟蹤由內(nèi)環(huán)實現(xiàn),，由圖2可看出,，內(nèi)環(huán)的輸入ω_d是外環(huán)控制的輸出，整個控制系統(tǒng)構(gòu)成閉環(huán)反饋結(jié)構(gòu),。下面分別設(shè)計外環(huán)和內(nèi)環(huán)控制器,。

2.1 外環(huán)控制器設(shè)計

    外環(huán)主要用于實現(xiàn)姿態(tài)角跟蹤，并產(chǎn)生姿態(tài)角速度指令ω_d,，四旋翼動力學(xué)模塊反饋給內(nèi)環(huán)的為實際姿態(tài)角速度ω=(p，q,，r)^T,，將ω_d與ω的差值作為內(nèi)環(huán)的輸入，控制的最終目標(biāo)是使ω=ω_d,，這樣便可以實現(xiàn)無靜差跟蹤期望姿態(tài)角的控制,，所以可以設(shè)計外環(huán)的積分滑模面如下：

其中參數(shù)K₁=diag{k₁₁，k₁₂,，k₁₃},。需要確定合適的K₁，以使姿態(tài)角跟蹤指令偏差γ_e較快地滑動至穩(wěn)定,。

    對式(5)微分計算,，得：

2.2 內(nèi)環(huán)控制器設(shè)計

3 仿真與實驗分析

    本文基于實驗室搭建的硬件實驗平臺在MATLAB仿真環(huán)境^[10]下對設(shè)計的算法進(jìn)行驗證，并與文獻(xiàn)[2],、[4]中采用的PID和反步法設(shè)計的姿態(tài)控制器控制效果進(jìn)行對比,。

3.1 實驗平臺

    將基于Pixhawk飛控板的四旋翼無人機(jī)實驗平臺作為研究對象。選用尼龍加纖維的機(jī)架搭建飛行器,，機(jī)身為X型構(gòu)架,，機(jī)架的對角軸距為35 cm；采用STM32F427為機(jī)載主控單元,。姿態(tài)感測傳感器包括三軸16位ST Micro L3GD20H陀螺儀,，用于測量旋轉(zhuǎn)速度；三軸14位加速度計和磁力計,，用于確認(rèn)外部影響和羅盤指向,；MEAS MS5611氣壓計，可外接UBLOX LEA GPS,，用于確認(rèn)飛行器絕對位置,。選取無刷電機(jī)型號為MT2312-960 KV,，提供動力輸出，電池容量為5 000 mA,，最大放電電流為30 A,，內(nèi)置電壓電流傳感器，以確認(rèn)電池狀況,。該飛行器遙控器型號為樂迪AT9,，對應(yīng)的接收器型號為2.4G、9通道的R9D,；地面站軟件采用3DR推薦的專為PX4/PIXHAWK設(shè)計的新的QGroundControl,。在該環(huán)境下對飛行器進(jìn)行控制算法驗證和調(diào)試。

3.2 實驗結(jié)果

    由此硬件實驗平臺確定的實驗參數(shù)如下：轉(zhuǎn)動慣量分別為J_xx=J_yy=0.32 kg·m²,，J_zz=0.63 kg·m²,，轉(zhuǎn)動慣量不確定項不妨假設(shè)為ΔJ_xx=ΔJ_yy=ΔJ_zz≈0.05，根據(jù)分析和仿真實驗效果可確定ρ₁=5,，ρ₂=1.5,，μ=10，增益矩陣K₁=diag{0.3 0.3 0.3},，K₂=diag{1 1 1},。由于復(fù)雜環(huán)境下飛行器面臨受擾影響的多樣性，需要考慮隨機(jī)干擾力矩對3個軸向控制力矩的影響,，故3個軸向添加隨機(jī)干擾力矩d=[rand( ),，rand( )，rang( )]^T,，3個姿態(tài)初始角和初始角速度均為0,，控制指令取余弦信號。

    搭建的Simulink仿真模塊如圖3所示,。該仿真系統(tǒng)包括以下五部分：控制指令,、外環(huán)控制模塊、內(nèi)環(huán)控制模塊,、四旋翼動力學(xué)模塊,、指令跟蹤輸出。

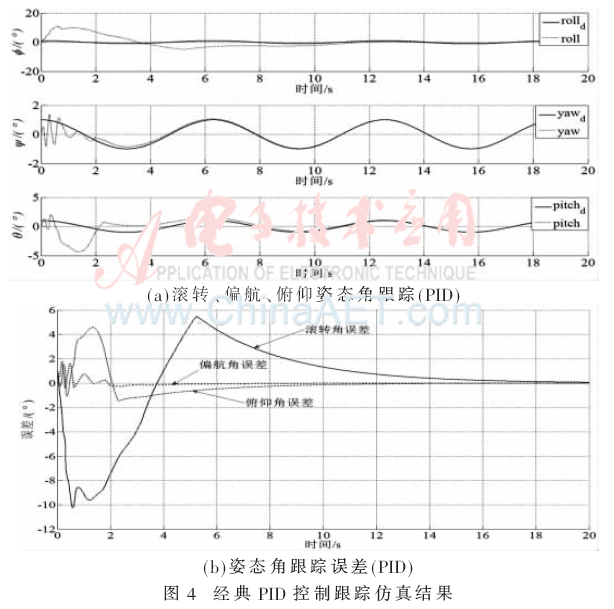
    (1)采用PID控制的跟蹤結(jié)果如圖4所示,。

    (2)采用（Back-Stepping）反步法控制跟蹤結(jié)果如圖5所示,。

    (3)采用雙環(huán)滑模控制跟蹤結(jié)果如圖6所示,。

    圖4(a)是用PID方法設(shè)計的姿態(tài)控制器用于跟蹤三個姿態(tài)角仿真圖形,，由誤差波形圖4(b)可看出，飛行時間前5 s內(nèi)的滾轉(zhuǎn)角跟蹤誤差由-10°～5°變化，俯仰角誤差在1.7 s時最大達(dá)到4.8°,，偏航角跟蹤誤差則在-1°~1.5°范圍內(nèi)變化,，俯仰和偏航角在8 s跟蹤上期望指令，而滾轉(zhuǎn)角需16 s左右才跟蹤上期望信號,。圖5是用反步法設(shè)計姿態(tài)控制器的跟蹤效果,，滾轉(zhuǎn)角誤差最大為4°，俯仰角誤差最大為3°,，偏航誤差則最大為2°,，俯仰和偏航角在6 s跟蹤上期望指令，滾轉(zhuǎn)角在12 s時能跟蹤上期望指令信號,，與PID效果相比,，性能有所改善。圖6則是采用本文所提出的雙環(huán)滑模設(shè)計方案所設(shè)計的姿態(tài)控制器的姿態(tài)跟蹤仿真圖形,，由圖6的誤差曲線可看出,，滾轉(zhuǎn)角誤差最大達(dá)到0.38°，俯仰角誤差最大0.1°,，偏航角誤差不到0.1°,，系統(tǒng)在6 s后能幾乎無靜差地跟蹤期望姿態(tài)角，穩(wěn)態(tài)誤差和響應(yīng)時間都十分理想,。由此可見，采用雙環(huán)滑模所設(shè)計的四旋翼姿態(tài)控制系統(tǒng)的三個姿態(tài)角能快速有效地跟蹤預(yù)先設(shè)定的期望角度指令,，控制性能較為理想,。

4 結(jié)束語

    本文為解決受擾動及參數(shù)不確定時的四旋翼姿態(tài)跟蹤穩(wěn)定問題，將雙環(huán)滑?？刂破饕胧芸叵到y(tǒng)中,，應(yīng)用雙環(huán)滑模變結(jié)構(gòu)跟蹤期望輸出，基于實驗室Pixhawk飛控板搭建的四旋翼硬件實驗平臺確定了相關(guān)實驗參數(shù),，在MATLAB/Simulink仿真環(huán)境中驗證該控制算法的可行性,，并與PID和反步法控制效果進(jìn)行了對比。仿真結(jié)果表明,，利用雙環(huán)滑模切換函數(shù)的方法設(shè)計四旋翼姿態(tài)控制器具有明顯的優(yōu)點,，即在參數(shù)不確定和存在外界擾動情況下能更加快速地跟蹤期望指令信號，且穩(wěn)態(tài)誤差保持在較小范圍內(nèi),，控制器的魯棒性和動態(tài)性能滿足實際飛行控制的指標(biāo)要求,。

參考文獻(xiàn)

[1] MILHIM A，Zhang Youmin,，RABBATH C A.Gain scheduling based PID controller for fault tolerant control of a quad-rotor UAV[C].AIAA,，2010，3530：1-13.

[2] LI J,，LI Y.Dynamic analysis and PID control for a quadrotor[C].Mechatronics and Automation(ICMA),，2011 International Conference on.IEEE,，2011：573-578.

[3] SALIH A L，MOGHAVVEMI M,，MOHAMED H A F,，et al.Flight PID controller design for a UAV quadrotor[J].Scientific Research and Essays，2010,，5(23)：3660-3667.

[4] 宋召青,，劉曉，趙賀偉.基于反演的四旋翼無人飛行器姿態(tài)自適應(yīng)控制[J].Machine Building & Automation,，Jun 2014,，43(3)：201-203.

[5] 叢夢苑.基于線性二次調(diào)節(jié)器的四旋翼飛行器控制系統(tǒng)的設(shè)計與研究[D].哈爾濱：哈爾濱工程大學(xué)，2011.

[6] BOUABDALLAH S,，SIEGWART R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C].Robotics and Automation,，2005.ICRA 2005.Proceedings of the 2005 IEEE International Conference on.IEEE，2005：2247-2252.

[7] MELLINGER D,，MICHAEL N,，KUMAR V.Trajectory generation and control for precise aggressive maneuvers with quadrotors[J].The International Journal of Robotics Research，2012,，31(5)：664-674.

[8] HE Y,，WANG L，JI S.Four-rotor robot trajectory tracking control based on model reference dynamic inversion[J].Modeling and Simulation,，2015,，4(1)：8-16.

[9] 董杰，賀有智.基于雙環(huán)滑模變結(jié)構(gòu)的彈頭姿態(tài)魯棒控制器設(shè)計[J].航天控制,，2011,，15(12)：64-67.

[10] 劉金琨.滑模變結(jié)構(gòu)控制MATLAB仿真[M].北京：清華大學(xué)出版社，2005.