摘 要： 在研究了Wu_Manber算法及其已有改進的基礎上,，在跳躍距離、匹配過程和并行處理三方面進行了綜合改進,。改進后的算法跳躍距離最大能達到m+1,，有效減少匹配過程中的比較次數(shù)，最后充分利用現(xiàn)有的硬件處理能力,，進行并行處理,，避免模式串集合過度增加后算法效率的下降問題，提高超大文本串的掃描速度,。
關鍵詞： 多模式匹配,；Wu_Manber算法
0 引言
多模式匹配問題可以描述為：P={p1， p2,，...,，pk}，是一個模式串的集合,，其中任意一個模式串pi都是由字符表Σ中的字符所組成,。T=t1，t2,，...,，tn是一個大文本串，ti屬于Σ,。求所有模式P在T中的所有出現(xiàn),。
多模式匹配算法一般是單模式匹配算法的推廣。單模式匹配算法中經典并且效率較高的算法主要有BM（Boyer Moore）算法[1]和QS（Quick Search）算法[2]等。多模式串匹配算法中,，Wu_Manber算法[3]是實際應用中平均性能最好的一個算法,。QS算法是對BM算法的改進。而Wu_Manber算法是BM算法的多模式擴展,?？梢哉f，這幾個算法的核心思想是一致的,。
多模式匹配過程要獲得高的效率,，關鍵在于三個方面：一是盡可能多、盡可能遠地進行跳躍,，避免進入無效的匹配過程,；二是在可能出現(xiàn)匹配時，盡量減少比較次數(shù),；三是綜合利用現(xiàn)有硬件條件,，進行并行運算。
在本文中,，使用p[0..m-1]表示要匹配的模式串,，長度為m。使用T=t[0..n-1]表示正文文本,，長度為n,。字符集以Σ表示，大小為σ,。將匹配過程中P與T中長度為m的子串之間的一次比較稱為一次嘗試,，并將T中的該子串稱為當前匹配窗口，假設當前匹配窗口在T中的起始位置為k,。
1 Wu_Manber算法
在多模式匹配中,，隨著模式串個數(shù)的增加，字符t[k+m]出現(xiàn)在各模式串尾端的概率相應增加,，因而能達到的平均跳躍距離隨之變小,，BM或QS算法的跳躍效果在多模式串的情況下被極大地削弱,。Wu_Manber 算法利用塊字符擴展了不良字符的跳躍效果,，同時用散列表來篩選匹配階段應進行匹配的候選模式串，減少算法匹配時間,。在每次匹配嘗試中,，一次考察一“塊”，即連續(xù)B個字符,。根據(jù)這B個字符所組成的塊的匹配情況來決定跳躍距離,。通常模式數(shù)量少的時候取B=2，模式數(shù)量大的時候取B=3,。
Wu_Manber算法同樣分為兩個處理階段,。預處理階段將建立三個表格：SHIFT表,、HASH表和PREFIX表。SHIFT表中存儲字符集中所有塊字符的跳躍距離,。HASH 表用來指出可能匹配的所有候選模式串,。PREFIX 表用來過濾候選模式串。
取所有模式串長度的最小值為m,，只考慮所有模式串的前m個字符,。假設當前匹配窗口的最后B個字符組成不良字符塊X：
⑴X在所有模式串中不出現(xiàn),，則跳躍距離為m-B+1,，即SHIFT[X]=m-B+1。
?、芚在部分模式串中出現(xiàn),，則跳躍距離為X在所有模式串中的最右出現(xiàn)到X的距離。
如果X是良好字符塊,，則SHIFT[X]＝0,，進入精確匹配過程。HASH[X]指向所有以X結尾的模式串列表,，依次訪問這些可能匹配的候選模式串,，如果模式串的前綴與PREFIX表不符合，則跳過,；否則比較該模式串中的每個字符以決定是否出現(xiàn)一個完全匹配(此時的比較不再限于模式串的前m個字符,，而是完整的模式串)。
以上的討論中,，SHIFT[X]和HASH[X]指的是先將X散列,，得到一個整數(shù)值，再用這個整數(shù)值作索引,，查詢SHIFT表和HASH表,。
Wu_ Manber算法的時間復雜度在最好的情況下能達到O(B×n/m)。
2 對Wu_Manber算法的改進
2.1 對跳躍距離的改進一
2.1.1 精確的不良字符塊跳躍距離
首先研究不良字符塊X在所有模式串中不出現(xiàn)時,，其跳躍距離是否只能達到m-B+1,。
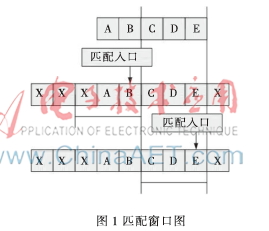
如圖1所示，假設“ABCDE”為模式串集中長度最小的模式,，此時匹配窗口的塊字符為“XAB”,，雖然“XAB”是個不良字符塊，但是它的后綴“AB”是模式“ABCDE”的前綴,，此時如果將匹配窗口移動m=5,，那么就會漏掉一次正確的匹配。長度為B的不良字符塊，至多它的長度為B-1的后綴可能在模式串中出現(xiàn),。因此安全的跳躍距離為m-(B-1)=m-B+1=3,。但是這種情況的出現(xiàn)次數(shù)相對于匹配中遇到的大多數(shù)不良字符塊轉移來說所占比例非常少，它減少了大多數(shù)情況下的跳躍距離,，因此可以引入精確的不良字符跳躍表Shift[ ],，其最大跳躍距離可以達到m。
精確的Shift[ ]計算過程：
?、?用m填寫Shift[ ]表,；
⑵for (i = 1 ,；i < B ,；i ++ )
{
對所有Bc ∈{ suffix(Bc，i) = prefix(pattern,，i) }
Shift [Bc ] = m - i ,；
}
⑶For 每一個關鍵詞
{
For 當前關鍵詞中的每一個塊字符
計算Shift[ Bc ] ,；
}
2.1.2 弱化的良好字符塊跳躍距離
Wu_Manber算法中沒有使用BM算法中使用的良好字符跳躍方法,，因此無論當前良好字符塊的匹配結果如何，跳躍距離都固定為1,。為此引入一種弱化了的良好字符塊跳躍表GBSShift[ ]來改進這一問題,。該表記錄了每一個模式串的長度為B的后綴(最后一個塊字符)在所有模式串中的所有非后綴出現(xiàn)位置與后綴的距離的最小值。這樣,，在匹配失敗后,，其跳躍距離很可能大于1。
實際試驗證明了在附加微小的預處理時間(約為原預處理時間的10%)后,，以上兩種改進能夠有效地降低比較次數(shù),，從而減少了對整個文本數(shù)據(jù)的掃描時間(約為原算法掃描時間的85%~92%) 。
2.2 對跳躍距離的改進二
結合Q S算法的思想,，忽略當前匹配窗口的信息,，不管匹配是否成功，直接使用字符塊t[m-B+1..m]來確定跳躍距離,。跳躍距離至少為1,，最大為m-B+2。但這樣做的話,，跳躍表就無法用來判斷當前窗口是否存在可能匹配了(原算法跳躍距離為0表明存在可能匹配,，應該進入精確匹配過程),。根據(jù)QS算法的特點,，其匹配順序沒有要求，因此可以查看各模式串的前B個字符(前綴)與當前窗口的前綴是否匹配。為此需要增加一個表Head [ ],，記錄各模式串前綴的信息,。Shift表記錄的是若當前文本與所有模式的前綴不同時， 數(shù)據(jù)指針向后跳躍距離,。
Shift [ ]表計算方法為：
?、?用m填寫Shift [ ]表；
?、艶or 每一個模式串
{ //對當前模式串中的每一個塊字符,， 這里B = 2，計算跳躍距離,；
for ( i= 0,； i< m - 1； i+ + )
{
Hash = hashBlock (pattern+ i) ,；
if (Shift[hash]> = m - 1- i)
Shift[hash]= m - 1- i,；
}
}
Head 表計算如下：
⑴ 用 0 預置 Head[ ]表,；
?、艶or 每一個模式串
{
hash = hashBlock (pattern) ；
Head[hash ] = 1,；
}
實驗結果顯示,， 在最小模式長度較小時，當 m<9時,，改進后的算法比原算法性能顯著提高,，用于英文文本時平均提高 8%~20%，用于中文文本時平均提高約15%~30%,；當最小模式長度較大時,， 改進后的算法性能與原算法基本相同。
2.3 對跳躍距離的綜合改進
以2.2節(jié)為基礎,，結合2.1節(jié)的思想,，計算其不良字符塊的精確跳躍距離，將使得最大跳躍距離能夠達到m+1,。另外,，同樣引入2.1節(jié)所使用的弱化的良好字符塊跳躍表。這樣,，改進后的算法思想為：在當前匹配窗口中,，如果根據(jù)Head[ ]表發(fā)現(xiàn)不可能出現(xiàn)匹配，則使用精確的不良字符塊跳躍表直接向右移動窗口,，其最大距離可達m+1,，否則,，進入精確匹配過程，比較順序為從右向左,。如果找到匹配則輸出,，再次采用精確的不良字符塊跳躍表直接向右移動窗口，否則比較不良字符塊跳躍表和弱化的良好字符塊跳躍表,，選取較大值作為窗口的跳躍距離,。
2.4 匹配過程改進一
進入精確匹配過程后，Wu_Manber 算法對HASH[X]指向的候選模式串列表進行逐個比較,。如果模式串pj和pk都匹配成功,，則pj是pk的后綴或者反之。稱存在一個模式是其他模式的后綴的一組模式為后綴模式,。例如模式this,、his、is,，如果沒有后綴模式,，就不可能有兩個模式串同時匹配成功，所以一旦某個模式串匹配成功,，就可以提前結束循環(huán),，根據(jù)跳躍表移動匹配窗口到下一個位置。
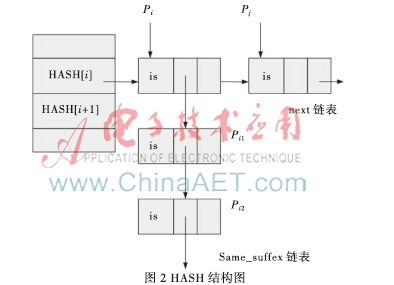
改進后的HASH數(shù)據(jù)結構增加了 same_suffix域,，如圖2,。后綴處理算法把后綴模式的模式使用same_suffix域鏈接起來，這樣在HASH表的next鏈表中的模式就不存在后綴模式,。圖2中,，Pi為is，Pi1為his,，Pi2為this,，Pi、Pi1,、Pi2構成一個后綴模式,，其中Pi是其他模式公共后綴；通過Pi的 same_suffix鏈表鏈接Pi1,、Pi2,。
改進后算法效率在模式的各個規(guī)模上都有明顯的提高，提高幅度達到8%~15%,，說明后綴模式處理能夠比較穩(wěn)定,、有效地提高算法的運行效率。
2.5 匹配過程改進二
由于 CPU進行一次8位的字符比較與進行一次機器字長的整數(shù)比較所花費的時間完全相同,，因此完全可以一次比較4個字符（32位CPU）,，以此提高效率,。
2.6 其他改進
算法在匹配過程中的最大“跳躍” 距離是由所有模式串中最短的模式串長度 m決定的。所以如果最小模式串的長度為1或2,，則最大跳躍距離將非常有限,，會大大降低算法的性能,。
實驗得出的數(shù)據(jù)為：當m=1時,，算法所用時間是其他情況下的7~10倍；m=2時,，算法所用時間是其他情況下的4~9倍,。針對這個問題，可以將模式串集一分為二,，長度小于等于2的為一組,，其他的為另一組。將算法在這兩個模式串子集上分別運行,，最后得到總結果,。
改進后的Wu_Manber算法性能有明顯提高。特別是對于英文匹配,，在單字節(jié)模式串出現(xiàn)個數(shù)較少時,，匹配速度較原來提高了 5~8倍?？紤]到現(xiàn)實中,，單字節(jié)(單漢字)模式串出現(xiàn)個數(shù)較少，所以這種改進還是具有一定的實用價值,。
2.7 并行處理
現(xiàn)在隨著CPU內核數(shù)的增多,，在算法實現(xiàn)時應充分利用其并行處理能力。
2.5節(jié)提出的問題和解決方法完全可以用兩個線程或進程同時并行處理,。不僅如此,，應將模式串集合合理分組，用多個線程或進程并行處理,，每個線程或進程負責處理一個模式串子集,，降低模式串集合過度增加后算法效率的下降。
大文本則切成數(shù)段,，每段之間有一定的重合,，保證不遺漏可能匹配，采用多個線程或進程同時處理,，每個線程或進程負責處理一段文本,，這樣在線程數(shù)不超過CPU核心數(shù)的前提下，超大文本串的掃描速度將以近似線性增加,。
3 結束語
多模式匹配算法是一個基礎算法,，有許多重要應用場合,，對其進行深入研究和試驗具有重要意義。通過對Wu_Manber算法的仔細研究,，在算法實現(xiàn)過程中對算法作出了多方面的改進,，在實際應用中，取得了良好的效果,。
參考文獻
[1] Boyer R S,，Moore J S. A fast string searching algorithm[J]. Communications of the ACM，1977(20)：762-772.
[2] SUNDAY D M. A very fast substring search algorithm[J]. Communications of the ACM,，1990, 33(8)：132-142.
[3] Sun Wu,，Manber U. A fast algorithm for multi pattern searching [R]. Technical Report TR94217，University of Arizona at Tuscon,， 1994.
[4] 楊東紅,，徐恪，崔勇.改進的Wu-Manber 多模式串匹配算法[J]. 清華大學學報 (自然科學版),，2006,，46(14)：109-112.
[5] 李雪梅，代六玲,，童新海,，等.對 QS串匹配算法的一種改進[J]. 計算機應用與軟件，2006,，23(3)：55-57.
[6] 張鑫,，譚建龍，程學旗.一種改進的Wu_Manber 多關鍵詞匹配算法[J]. 計算機應用,，2003,，23(7)：544-549.
[7] 孫曉山，王強,，關毅,，等.一種改進的 Wu_Manber 多模式匹配算法及應用[J]. 中文信息學報，2006,20(2)：47-53.
[8] 陳瑜,、陳國龍. Wu_Manber算法性能分析及其改進[J]. 計算機科學,，2006，33(16)：207-029.