《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 通信與網(wǎng)絡(luò) > 設(shè)計應(yīng)用 > 非標(biāo)準(zhǔn)約束恒模盲多用戶檢測的改進(jìn)算法研究
非標(biāo)準(zhǔn)約束恒模盲多用戶檢測的改進(jìn)算法研究
2015年電子技術(shù)應(yīng)用第6期
周先春1,，2,，3,，王 潔1,，2,，3,，孫文榮1,，2,，3
1.南京信息工程大學(xué) 電子與信息工程學(xué)院,， 江蘇 南京210044； 2.南京信息工程大學(xué) 江蘇省大氣環(huán)境與裝備技術(shù)協(xié)同創(chuàng)新中心,，江蘇 南京210044,； 3.南京信息工程大學(xué) 江蘇省氣象探測與信息處理重點實驗室，江蘇 南京210044
摘要： 針對碼分多址蜂窩移動通信中存在的多址干擾問題,，以瑞利分布為變步長,，構(gòu)造了基于瑞利分布變步長的非標(biāo)準(zhǔn)約束恒模算法；與差分形式相結(jié)合,，提出了基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法（RDV-NSCDCMA）,；分析了此算法的性能并與非標(biāo)準(zhǔn)約束恒模算法(NSCCMA)進(jìn)行了仿真比較。
中圖分類號： TN914.4
文獻(xiàn)標(biāo)識碼： A
文章編號： 0258-7998(2015)06-0081-03
Research on improved algorithm of non-standard constrained constant modulus for blind multiuser detection
Zhou Xianchun1,，2,，3，Wang Jie1,，2,，3，Sun Wenrong1,，2,，3
1.College of Electronic and Information Engineering, Nanjing University of Information Science & Technology, Nanjing 210044，China,； 2.Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science and Technology, Nanjing 210044, China,； 3.Jiangsu Key Laboratory of Meteorological Observation and Information Processing, Nanjing University of Information Science and Technology, Nanjing 210044, China
Abstract： In view of the problems about multiple access interference in CDMA(code division multiple access) cellular mobile communication, firstly we constructed a non-standard constrained constant modulus algorithm which is based on variable step of the Rayleigh distribution. Combined with the difference form, we put forward a non-standard constrained constant modulus algorithm of the difference form which is based on variable step of the Rayleigh distribution, called RDV-NSCDCMA. Compare with the simulations of the non-standard constrained constant modulus algorithm(NSCCMA) and RDV-NSCDCMA.
Key words : Rayleigh distribution；constant modulus algorithm,；blind multiuser detection,；non-standard constrained； difference

    

0 引言

    多用戶檢測技術(shù)是利用造成多址干擾的所有用戶的幅度,、用戶碼,、時延等信息來對用戶進(jìn)行檢測，以降低多址干擾,。而其中只需觀測數(shù)據(jù)序列的盲自適應(yīng)多用戶檢測,，因其復(fù)雜度低、效率高，是近年來移動通信相關(guān)領(lǐng)域的熱點研究課題,。恒模算法因?qū)崿F(xiàn)簡單,，且滿足收斂條件的恒模算法其收斂速度及穩(wěn)態(tài)性能較好，早已被應(yīng)用于多用戶檢測中,。雖存在一些問題,，例如存在多個局部收斂點、易收斂到局部最小點等,，但之后也出現(xiàn)了很多解決的方法[1-2],。恒模多用戶檢測算法應(yīng)用廣泛，存在于多個領(lǐng)域中[3-4],。

    由于標(biāo)準(zhǔn)約束恒模算法的性能受接收信號幅值參數(shù)的影響,，本文在非標(biāo)準(zhǔn)約束恒模盲多用戶檢測的基礎(chǔ)上，以瑞利分布為變步長,，結(jié)合差分形式構(gòu)造的差分恒模算法,，僅需知道兩相鄰信號的幅值差，避免了搜索具體期望用戶的信號幅值,，使算法更為簡單快捷,。

1 系統(tǒng)模型

    經(jīng)過AWGN信道后的K個用戶的同步直接序列擴(kuò)頻的碼分多址(Direct Sequence-Code Division Multiple Access，DS-CDMA)系統(tǒng),，其基帶接收信號為：

tx1-gs1-3.gif

2 非標(biāo)準(zhǔn)約束恒模算法

    基本的恒模算法(Constant Modulus Algorithm,，CMA)通常為了計算便捷取信號幅值ζ=1，此時代價函數(shù)為：

tx1-gs4-6.gif

    定義tx1-gs6-x1.gif由于ωTS1=d等價于ω=dS1+Bx,，將式(6)轉(zhuǎn)化為無約束優(yōu)化問題J(ω)=J(dS1+Bx),。

    利用最陡下降法可以得到非標(biāo)準(zhǔn)約束恒模的自適應(yīng)算法[5]公式為：

tx1-gs7.gif

3 基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法

    由式(7)可以看出：若步長μ值較大，則每次迭代時權(quán)系數(shù)的幅值調(diào)整就大,，此時收斂速度較快,，穩(wěn)態(tài)剩余誤差較大；若步長μ值較小,，則每次迭代時權(quán)系數(shù)的幅值調(diào)整就小,，此時收斂速度較慢，穩(wěn)態(tài)剩余誤差較小,。由于以上所述的非標(biāo)準(zhǔn)約束恒模算法（NSCCMA）采用的是固定步長μ，這樣使得恒模算法的性能無法很好地兼顧,，應(yīng)用就會受到很大限制,。采用時變步長來代替固定步長就能很好地解決這一矛盾。步長值應(yīng)根據(jù)以下原則調(diào)整：首先在未知的一些系統(tǒng)參數(shù)變化時或初始收斂的階段,，當(dāng)步長較大時,，它的收斂速度和對于時變系統(tǒng)的跟蹤速度才會快；而當(dāng)算法收斂后，不論干擾信號的大小及步長都應(yīng)保持較小值,，這樣穩(wěn)態(tài)失調(diào)噪聲才會小,。

    基于瑞利分布的變步長取步長函數(shù)公式如下：

    tx1-gs8.gif

式中，參數(shù)α和參數(shù)β>0分別控制函數(shù)的形狀和函數(shù)的取值范圍,。分析式(8)可知：誤差函數(shù)|e(n)|在初始收斂階段較大時,，對應(yīng)的步長μ(n)就較大，此時算法的收斂速度較快,；當(dāng)算法已達(dá)到或即將到達(dá)穩(wěn)態(tài)時,，此時誤差函數(shù)|e(n)|趨近于零，對應(yīng)的步長μ(n)就變得很小,，此時算法的穩(wěn)態(tài)誤差就很小,。由此，可取式(8)為基于瑞利分布變步長的步長函數(shù)公式,?；谌鹄植甲儾介L的非標(biāo)準(zhǔn)約束差分恒模算法(Rayleigh distribution variable-step--non-standard constrained differential constant modulus algorithm，RDV-NSCDCMA)取代價函數(shù)為：

tx1-gs9-12.gif

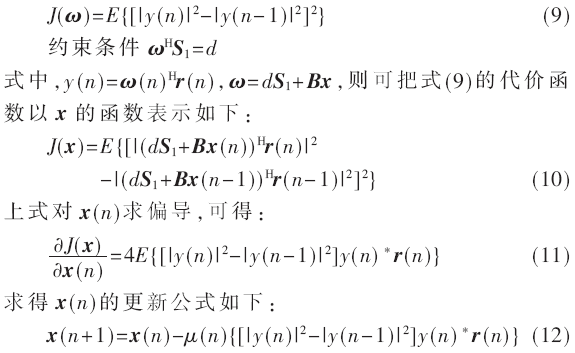
式中,，變步長公式為μ(n)=β{[|e(n)|/α2]exp[-e(n)2/(2α2)]},，式中參數(shù)α及參數(shù)β的最優(yōu)值應(yīng)根據(jù)具體仿真來確定。本次仿真中,，α=150,，β=0.006，此時RDV-NSCDCMA算法達(dá)到最佳收斂,。

4 性能仿真

    本仿真采用MATLAB軟件對非標(biāo)準(zhǔn)約束恒模算法（NSCCMA）和基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法（RDV-NSCDCMA）進(jìn)行仿真,。令用戶1為期望用戶，采用31位Gold序列為各用戶的擴(kuò)頻碼,，其擴(kuò)頻增益N=31,，輸入信號為二進(jìn)制相移鍵控(Binary Phase Shift Keying，BPSK)調(diào)制,。取d=10,，期望用戶的信號幅度A1=0.1。

    仿真一：以信噪比與誤碼率的關(guān)系曲線圖為測度基準(zhǔn),，研究比較非標(biāo)準(zhǔn)約束恒模算法與基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法的抗多址干擾能力,。本仿真中分別取干擾用戶數(shù)為K=5和K=10，圖1中干擾用戶相對于目標(biāo)用戶的多址干擾強(qiáng)度均為10 dB,，圖2中干擾用戶相對于目標(biāo)用戶的多址干擾強(qiáng)度均為20 dB,。取總迭代次數(shù)為N=1 000。

tx1-t1.gif

tx1-t2.gif

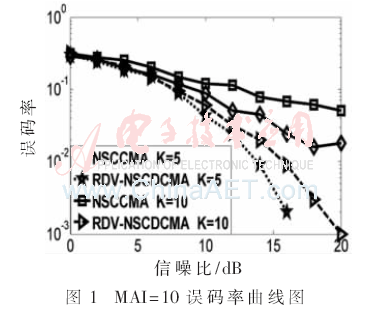
    由仿真曲線圖1和圖2可以看出：當(dāng)干擾用戶數(shù)為5時,，兩條曲線的差距在信噪比大于10 dB時尤其明顯,，說明此時基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法的誤碼率的改善非常明顯,。當(dāng)干擾用戶數(shù)增到10時，曲線的差距在信噪比取值0 dB～20 dB的絕大部分區(qū)間上都較大,，即整個區(qū)間上基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法的誤碼率的改善都較為明顯,。

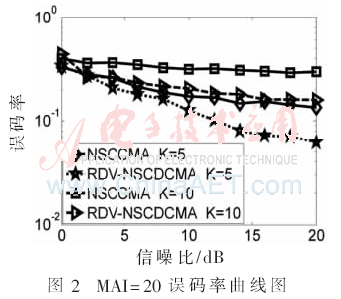
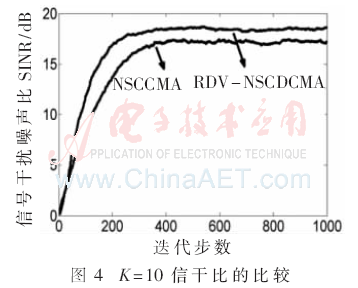
    仿真二：以信干噪比與迭代次數(shù)的關(guān)系曲線圖為測度基準(zhǔn)，研究比較非標(biāo)準(zhǔn)約束恒模算法與基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法的抗遠(yuǎn)近效應(yīng)能力,。本仿真中分別取干擾用戶數(shù)為K=5和K=10,，干擾用戶相對于目標(biāo)用戶的多址干擾強(qiáng)度為20 dB，信噪比為20 dB,，總迭代次數(shù)為N=1 000,。

    由仿真曲線圖3、圖4可以看出：當(dāng)干擾用戶數(shù)為5時,，基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法在迭代次數(shù)到達(dá)100時趨于穩(wěn)定,，其信干噪比穩(wěn)定值為19 dB； 而非標(biāo)準(zhǔn)約束恒模算法在迭代次數(shù)到達(dá)200時趨于穩(wěn)定,，其信干噪比穩(wěn)定值為18 dB,。當(dāng)干擾用戶數(shù)為10時，基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法在迭代次數(shù)到達(dá)300時趨于穩(wěn)定,，其信干噪比穩(wěn)定值為18.5 dB,； 而非標(biāo)準(zhǔn)約束恒模算法在迭代次數(shù)到達(dá)400時趨于穩(wěn)定，其信干噪比穩(wěn)定值為17 dB,。即無論在個干擾用戶還是個干擾用戶情況下,，基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法的收斂速度和穩(wěn)定性能都優(yōu)于非標(biāo)準(zhǔn)約束恒模算法。

tx1-t3.gif

tx1-t4.gif

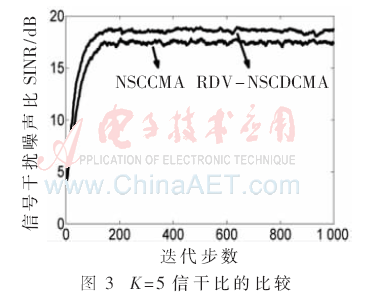
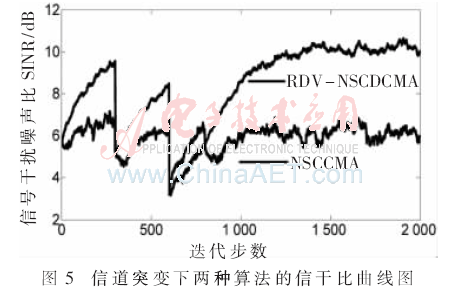
    仿真三：以信道突變時信干噪比與迭代次數(shù)的關(guān)系曲線圖為測度基準(zhǔn),，研究比較非標(biāo)準(zhǔn)約束恒模算法與基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法的信道跟蹤能力,。本仿真中取初始干擾用戶數(shù)為15，其中10個用戶的干擾強(qiáng)度為10 dB,，5個用戶的干擾強(qiáng)度為15 dB,。取信噪比為10 dB，總迭代次數(shù)為2 000次,，其他初始條件設(shè)置與仿真一中相同,。當(dāng)?shù)螖?shù)為300時，在上述基礎(chǔ)上再加入3個干擾強(qiáng)度為10 dB的用戶,；迭代次數(shù)為600時,，在上述基礎(chǔ)上去掉2個干擾強(qiáng)度為10 dB的干擾用戶，同時加入2個20 dB的干擾用戶,；迭代次數(shù)為800時,，在上述基礎(chǔ)上去掉2個干擾強(qiáng)度為20 dB的干擾用戶。

    由圖5可以看出：當(dāng)?shù)螖?shù)為300時,，本文提出的RDV-NSCDCMA算法的信干噪比值趨于10 dB,，而NSCCMA算法的信干噪比值趨于7 dB；當(dāng)?shù)螖?shù)為600時,， RDV-NSCDCMA算法的信干噪比值趨于8 dB,，而NSCCMA算法的信干噪比值趨于6 dB；當(dāng)?shù)螖?shù)為800時,，RDV-NSCDCMA算法的信干噪比值趨于10 dB,，而NSCCMA算法的信干噪比值趨于6 dB。即在整個2 000次迭代過程中,，當(dāng)?shù)螖?shù)分別為300次,、600次、800次時改變干擾用戶的個數(shù)和強(qiáng)度,，不論在高信噪比還是低信噪比下,，基于瑞利分布變步長的非標(biāo)準(zhǔn)約束差分恒模算法的跟蹤能力都強(qiáng)于非標(biāo)準(zhǔn)約束恒模算法。

tx1-t5.gif

5 結(jié)論

    本文以誤差函數(shù)e(n)為隨機(jī)變量的瑞利分布變步長μ(n),，調(diào)整參數(shù)α和參數(shù)β>0可以分別改變函數(shù)的形狀和函數(shù)的取值范圍,；而非標(biāo)準(zhǔn)約束恒模算法不受接收信號幅值的影響，對碼分多址蜂窩移動通信中的多址干擾的改善能力也更強(qiáng),；差分恒模算法僅需知道兩相鄰信號的幅值差,，避免了搜索具體期望用戶的信號幅值，使算法更為簡單快捷,。將以此構(gòu)造的基于瑞利分布變步長的非標(biāo)準(zhǔn)約束恒模算法與差分恒模相結(jié)合,，提出了RDV-NSCDCMA 算法。仿真結(jié)果表明, 即使在低信噪比強(qiáng)多址干擾的情況下,，本文提出的RDV-NSCDCMA算法在抗多址干擾能力,、抗遠(yuǎn)近效應(yīng)能力以及信道跟蹤能力方面均優(yōu)于非標(biāo)準(zhǔn)約束恒模算法（NSCCMA)。

參考文獻(xiàn)

[1] ELNASHAR A,，ELNOUBI S,，ELMIKATI H.Sample-by-sample and block-adaptive robust constant modulus-based algorithms[J].IET Signal Processing，2012,，6(8)：805-813.

[2] 夏偉娟,，朱立東.一種分?jǐn)?shù)低階統(tǒng)計量廣義恒模盲多用戶檢測算法[J].信號處理，2010,，26(10)：1510-1514.

[3] Feng He,，Gunawan E，Yongliang Guan.Improved two-stage CMA-based blind receivers for joint equalization and multiuser detection[J].IET Communications,，June 2012：1131-1136.

[4] 張江,，張杭，崔志富,，等.異步DS-CDMA系統(tǒng)中的盲聯(lián)合干擾消除與多用戶檢測[J].信號處理,，2013,，29(6)：668-676.

[5] 郭江鋒.基于變步長理論盲多用戶檢測的研究[D].太原：太原理工大學(xué)，2006.

此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。