0 引言

　　圖像分割是圖像分析中一個核心技術(shù),，是計算機視覺研究中最重要的研究內(nèi)容,。目前常用的圖像分割方法有：閾值法、邊緣檢測法,、區(qū)域分割法,、聚類分析法和基于特定理論的圖像分割方法[1]。其中聚類分析法能夠以像素樣本之間的相似性準則來衡量分類結(jié)果,，目前應(yīng)用最廣的是由Bezkek提出的模糊C均值聚類算法(Fuzzy C-Means,，F(xiàn)CM)[2]。FCM聚類算法可以有效地解決圖像中存在的不確定性和模糊性等問題,，具有實現(xiàn)簡單和無監(jiān)督的特點,。然而,，目前常用的FCM聚類算法仍有亟待解決的問題：(1)FCM聚類算法對初始聚類中心或隸屬度矩陣具有較強的依賴性，搜索中極易陷入局部最優(yōu)解,；(2)FCM聚類算法抗噪性能較差,，算法的魯棒性不強；(3)該算法基于逐點像素進行圖像分類,，數(shù)據(jù)樣本較多時運算量大,，且只利用了圖像的灰度信息而忽略了像素的空間特征，導(dǎo)致算法收斂速度慢,?；诖耍墨I[3]結(jié)合直方圖信息,，降低了數(shù)據(jù)樣本計算量,。文獻[4]根據(jù)灰度和空間信息的相似性度量，對圖像的細節(jié)信息有一定的保留,。文獻[5]利用蟻群算法的全局優(yōu)化能力,，避免FCM算法陷入局部極值。然而,，對于受不同類型和不同程度噪聲影響的大規(guī)模像素樣本,，上述改進算法對噪聲的魯棒性較弱，算法的實時性較差,。

　　針對上述問題,，本文提出一種基于蟻群和自適應(yīng)濾波的模糊聚類圖像分割方法。該算法首先利用改進的蟻群算法對圖像進行初次分割,；然后采用自適應(yīng)中值濾波,，對不同類型和不同程度噪聲自適應(yīng)地調(diào)整濾波性能，提高該算法的魯棒性,；最后用圖像的直方圖特征空間優(yōu)化FCM算法的目標函數(shù),，減少數(shù)據(jù)運算量，加快收斂速度,，提高分割精度,。

1 傳統(tǒng)FCM算法概述

　　假設(shè)圖像樣本數(shù)據(jù)集X={x1，x2,，…,，xn}，n是圖像像素個數(shù),，將圖像劃分為c類。FCM聚類算法以圖像像素和聚類中心間的加權(quán)相似性測度,，對目標函數(shù)進行迭代優(yōu)化以獲得最優(yōu)聚類結(jié)果[6],。其目標函數(shù)[7]為：

　　其約束條件為：

　　其中,，uij是樣本點xj屬于第i類的隸屬度值，dij=||xj-vi||2是樣本點xj與聚類中心vi的歐式空間距離,，m是模糊加權(quán)指數(shù),。為了使目標函數(shù)J最小，利用拉格朗日數(shù)乘法得到隸屬度uij和聚類中心vi分別為：

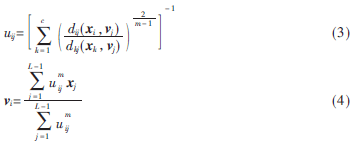
　　在迭代過程中,，由于傳統(tǒng)FCM采用下降算法,，受初始聚類中心或隸屬度矩陣的影響，需預(yù)設(shè)聚類類別數(shù),，這導(dǎo)致易收斂到局部極值,，且當樣本數(shù)目較多、圖像噪聲較大時,，會影響分割的實時性,。

2 基于蟻群和自適應(yīng)的FCM的圖像分割

　　2.1 蟻群算法的初始聚類中心設(shè)置

　　蟻群算法[8]具有較強的正反饋能力、全局性以及易于與其他算法融合等優(yōu)點,，尤其是其分布式并行計算機制以及優(yōu)化模糊聚類的特點,，能彌補FCM算法隨機選取初始聚類中心的不足。本文首先利用蟻群算法,，對圖像進行初次分割,，并得到初始聚類中心，作為FCM的初始參數(shù),。由于蟻群算法中,，圖像的每個像素都要與其余像素進行路徑選擇概率和距離計算，導(dǎo)致搜索進程慢,。因此,，本文將圖像的每個像素設(shè)為由灰度、梯度和鄰域表示的三維向量,，以此向量表示單個螞蟻,。因為像素能在灰度值上明顯區(qū)分目標和背景，梯度可以反映像素灰度值在邊界或噪聲點處的突變情況,，鄰域能體現(xiàn)出噪聲的特點[9],。并設(shè)置對應(yīng)的蟻群初始聚類中心特征，選取灰度直方圖的峰值點作為聚類中心的灰度特征,，像素梯度值0和圖像最大梯度列的均值作為聚類中心的梯度特征,，并根據(jù)像素梯度值設(shè)置聚類中心的鄰域特征。在此基礎(chǔ)上,，直接計算螞蟻像素與聚類中心的路徑選擇概率和距離,，以減少螞蟻搜尋的盲目性，降低計算量,，加快聚類進程,。

　　2.2 蟻群算法的聚類初值設(shè)置

　　對于原始圖像X,，將其每一個像素X={X|xi=(xi1，xi2,，…,，xim)，i=1,，2,，…，N,，N=m×n}作為單個螞蟻,，螞蟻需聚集到j(luò)個聚類中心Cj，Xi到Cj的加權(quán)歐式距離為：

　　其中,，m是螞蟻像素的維數(shù),，P是權(quán)重因子，根據(jù)像素各分量對聚類的影響程度設(shè)定,。

　　設(shè)r為聚類半徑,，螞蟻像素Xi到聚類中心Cj的路徑上的信息素為：

　　螞蟻像素Xi選擇聚類中心Cj的概率為：

　　其中，S∈{Xs|dsj≤r,，s=1,，2，…,，N}表示分布在聚類中心Cj內(nèi)數(shù)據(jù)的集合,。?琢和?茁分別是影響因子，代表螞蟻聚類過程中信息素和啟發(fā)引導(dǎo)函數(shù)對路徑選擇的影響,。根據(jù)相關(guān)研究[10],，在此設(shè)置ij為啟發(fā)式引導(dǎo)函數(shù)，反映像素與聚類中心的相似度,。由于存在像素與聚類中心距離為零的情況,，為了保證引導(dǎo)函數(shù)不為無窮大，防止算法過早收斂,，本文在引導(dǎo)函數(shù)公式的分母加上1,，表示為：

　　在螞蟻搜尋過程中，計算轉(zhuǎn)移概率Pij,，選取最大轉(zhuǎn)移概率Pmax并標記對應(yīng)的螞蟻Xi,，將Xi歸并到Xj鄰域Cj內(nèi)，并更新信息素ij(t+1),?？紤]到螞蟻在路徑上產(chǎn)生的信息素增量存在動態(tài)蒸發(fā)的情況，本文采用一種新的信息素更新公式：

　　其中，是信息蒸發(fā)因素,，ij(t)是本次循環(huán)路徑上信息素的增量,。更新聚類中心為：

　　計算各類的類間距,，若類間距小于閾值e,，則將兩類合并后更新聚類中心。若迭代次數(shù)達到上限,，則轉(zhuǎn)到式(8),，否則輸出聚類中心vj和聚類個數(shù)c。

　　2.3 基于自適應(yīng)直方圖優(yōu)化的FCM

　　傳統(tǒng)FCM算法易受噪聲干擾,，分割數(shù)據(jù)樣本為圖像逐點像素,，其特征為灰度，導(dǎo)致樣本數(shù)目大,，且樣本數(shù)目會隨圖像大小的增大而增多,，從而影響圖像分割的實時性。針對以上不足,，本文利用自適應(yīng)直方圖優(yōu)化的FCM圖像分割算法,，以實現(xiàn)最優(yōu)的分割結(jié)果。

　　自適應(yīng)中值濾波器[11]具有保留圖像邊界和圖像高頻部分的特點,，本文采用自適應(yīng)中值濾波,，根據(jù)噪聲類型和噪聲程度，自適應(yīng)地調(diào)整濾波窗口的尺寸,，降低圖像噪聲干擾,，提高分割質(zhì)量。設(shè)Wxy為像素點(i,，j)濾波窗口,，Iij為像素點(i,，j)的灰度,，Imin為Wxy中的最小灰度值,，Imax為Wxy中的最大灰度值，Imed為Wxy中的灰度中值,，Wmax為最大濾波窗口,，W0為初始濾波窗口。自適應(yīng)中值濾波算法步驟如下：

　　(1)若Imin<Imed<Imax,，則表示Imed不是噪聲點，轉(zhuǎn)到步驟(2),，否則轉(zhuǎn)步驟(3),。

　　(2)若Imin<Iij<Imax,，則表示Iij不是噪聲點,，直接輸出Iij，否則輸出Imed,。

　　(3)增加濾波窗口Wxy尺寸，若Wxy≤Wmax,，則重復(fù)步驟(1)，否則輸出Iij,。

　　在此基礎(chǔ)上，將圖像從像素空間映射到其灰度直方圖特征空間，得到各灰度級出現(xiàn)的概率H(j),，則直方圖FCM[12]的目標函數(shù)為：

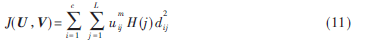
　　其中，L為灰度級,，取值范圍為0~255,，則待分類的圖像樣本集為X={0，1,，…,，L-1},。以此大幅度減少分類樣本數(shù)目，只有灰度級0~255個,，并且樣本數(shù)目不會隨圖像尺寸的增大而改變,，提高了算法的收斂速度,。在此基礎(chǔ)上,，利用拉格朗日乘子法得出隸屬度函數(shù)更新機制為：

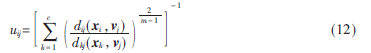
　　聚類中心的更新公式優(yōu)化為:

　　本文算法流程歸納如下：

　　(1)輸入圖像，根據(jù)蟻群聚類算法尋找初始聚類類別數(shù)和初始聚類中心,。

　　(2)設(shè)置自適應(yīng)中值濾波初始濾波窗口大小,，設(shè)置直方圖優(yōu)化的FCM聚類算法的類別數(shù)和初始聚類中心,、誤差閾值?著,、模糊指數(shù)m,、迭代次數(shù)iter。

　　(3)根據(jù)式(12)更新隸屬度uij,。

　　(4)根據(jù)式(13)更新聚類中心vi,。

　　(5)計算聚類中心誤差，若||V(i+1)-V(i)||<?著,，則算法結(jié)束；否則t=t+1,，并返回步驟(2)繼續(xù)執(zhí)行算法。

3 實驗結(jié)果與分析

　　為了評價算法的分割效率,，本文選用分辨率為405×405的lena灰度圖,，對標準FCM算法和ACOAFCM算法在不同類型和不同程度噪聲下進行驗證。本文實驗的測試硬件為主頻2.67 GHz,、內(nèi)存2GB的PC,，測試平臺為Windows XP操作系統(tǒng)，測試環(huán)境為MATLAB 7.10,。實驗設(shè)置的蟻群算法參數(shù)為r=100,，濾波窗口大取3×3，直方圖優(yōu)化FCM參數(shù)為m=2,，?著=10-5,，c=2。實驗分割結(jié)果如圖1所示,。

　　在圖1所示的圖像分割結(jié)果中,，從(a2)、(a3)中可看出,，當無噪聲時,，引入改進的蟻群信息素機制，使得ACOAFCM聚類效果更明顯,，人物與后方背景有明顯的區(qū)分,，臉部輪廓分割更清晰，頭發(fā)下端的細節(jié)好于標準FCM的分割結(jié)果,。從(b2),、(b3)中可見，當添加高斯噪聲時,，標準FCM算法分割效果不明顯且遺留較多噪聲,；而引入自適應(yīng)中值濾波的ACOAFCM算法分割結(jié)果中，雖然因高斯噪聲本身的特點,，存在局部噪聲點,，但仍保留了目標的邊界和高頻部分，整體分割效果與標準FCM相比有很大改善,。從(c2),、(c3)中可知,，當添加更高程度的椒鹽噪聲時，標準FCM分割結(jié)果中蝴蝶和花叢背景無明顯區(qū)分,；而ACOAFCM算法根據(jù)噪聲類型自適應(yīng)調(diào)整濾波性能,，不僅能克服噪聲干擾，避免算法陷入局部極優(yōu)值,，而且保留了蝴蝶的細節(jié)部分,，保持了較好的分割精度。從(b)和(c)可以看出,，本文算法對不同噪聲和不同程度的噪聲都有較強的魯棒性,。

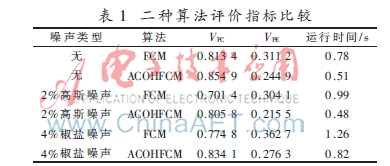
　　為了定量評價分割的有效性和實時性，本文采用評價指標：劃分系數(shù)VPC和劃分熵VPE,，分別表示聚類程度和聚類結(jié)構(gòu),，劃分系數(shù)VPC越大、劃分熵VPE越小,，則模糊聚類分割效果越好,。比較結(jié)果如表1所示，可見ACOAFCM算法對于抑制噪聲的指標值明顯優(yōu)于標準FCM算法,。此外，從表1收斂時間看出,，由于改進的蟻群算法快速地提供了最優(yōu)初始聚類中心,，且直方圖特征優(yōu)化了FCM算法，減少了樣本集,，ACOAFCM算法的速度明顯加快,。

4 結(jié)束語

　　本文提出了一種基于蟻群和直方圖的模糊聚類圖像分割算法，將蟻群算法與自適應(yīng)直方圖優(yōu)化的FCM算法相結(jié)合,。利用蟻群算法的魯棒性,、全局尋優(yōu)性和進化模糊聚類的優(yōu)點，得到FCM算法初始化的聚類中心,，有效地解決了模糊聚類算法易陷入局部最優(yōu)解,、對初始聚類中心依賴的問題。采用自適應(yīng)中值濾波,，能夠自適應(yīng)地根據(jù)噪聲類型和強度調(diào)整濾波性能,，增強FCM算法的魯棒性。引入圖像的直方圖特征空間優(yōu)化FCM算法的目標函數(shù),，減少圖像樣本數(shù)目,，降低了運算量。實驗結(jié)果表明,，本文的算法與傳統(tǒng)的FCM算法相比,，加快了圖像聚類收斂速度,，提高了圖像分割精度。

　　參考文獻

　　[1] 沙秋夫,，劉海賓,，何希勤，等.基于鄰域的模糊C-均值圖像分割算法[J].計算機應(yīng)用研究,，2007,，24(12)：379-385.

　　[2] BEZDEK J C，HATHAWAY R J.Convergence and theory forfuzzy C-means clustering：counter examples and repa[J].IEEETransactions Pattern Analysis and Machine Intellig-ence,，1987,，17(5)：873-877.

　　[3] TIAN M L，YANG J M.Pre-processing of froth image of  coal flotation based on weighted fuzzy C-means clustering by one-dimensional histogram[J].IEEE International Con-ference on Computing,，Measurement,，Control and Sensor Network，2012,，10(32)：396-400.

　　[4] STELIOS K,，VASSILIOS C.A robust fuzzy local informationC-Means clustering algorithm[J].IEEE Transction on Image Processing，2010,，19(5)：1328-1337.

　　[5] KARNAN D M,，GOPAL N N.Hybrid markov random field with parallel ant colony optimization and fuzzy C-means forMRI brain image segmentation[J].IEEE International Conference on Computational Intelligence and Computing Research，2010,，30(12)：1-4.

　　[6] 張翡,，范虹.基于模糊C均值聚類的醫(yī)學圖像分割研究[J].計算機工程與應(yīng)用，2014,，50(4)：144-151.

　　[7] 陳志飛,，時宏偉.基于均值漂移和模糊C均值聚類的圖像分割算法[J].計算機應(yīng)用與軟件，2013,，30(11)：14-17.

　　[8] 李積英,，黨建武.量子蟻群聚類模糊算法在圖像分割中的應(yīng)用[J].光電工程，2013,，40(1)：126-131.

　　[9] ZHANG W J,，LIU L，HAN Y H.An image segmentation approach based on ant colony algorithm[J].IEEE Interna-tional Congress on Image and Signal Processing,，2010,，30(15)：1313-1315.

　　[10] 楊立才，趙莉娜,，吳曉晴.基于蟻群算法的模糊C均值聚類醫(yī)學圖像分割[J].山東大學學報：工學版,，2007，37(3)：51-54.

　　[11] JIANG J F,，JING S.An effective adaptive median filter algorithm for removing salt & pepper noise in images[J].IEEE Photonics and Optoelectronic,，2010,，18(4)：244-248.

　　[12] ZHOU S Y，XIE W L,，GUO C X.A modified color imagesegmentation method based on FCM and region merging[C].2011 International Conference on Multimedia Technology(ICMT),，2011：3810-3813.